Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T03:00:31.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications of a New Separator Theorem for String Graphs

Published online by Cambridge University Press:  25 October 2013

JACOB FOX  and
JÁNOS PACH
JACOB FOX
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA (e-mail: fox@math.mit.edu)
JÁNOS PACH
Affiliation:
École Polytechnique Fédérale de Lausanne, Station 8, CH-1015 Lausanne, Switzerland and Rényi Institute, Hungarian Academy of Sciences, PO Box 127, H-1364 Budapest, Hungary (e-mail: pach@cims.nyu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

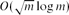An intersection graph of curves in the plane is called a string graph. Matoušek almost completely settled a conjecture of the authors by showing that every string graph with m edges admits a vertex separator of size $O(\sqrt{m}\log m)$. In the present note, this bound is combined with a result of the authors, according to which every dense string graph contains a large complete balanced bipartite graph. Three applications are given concerning string graphs G with n vertices: (i) if Kt ⊈ G for some t, then the chromatic number of G is at most (log n)O(log t); (ii) if Kt,t ⊈ G, then G has at most t(log t)O(1)n edges,; and (iii) a lopsided Ramsey-type result, which shows that the Erdős–Hajnal conjecture almost holds for string graphs.

Keywords

Primary 05C35Secondary 05C6252C10
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 1 , January 2014 , pp. 66 - 74
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ackerman, E. (2009) On the maximum number of edges in topological graphs with no four pairwise crossing edges. Discrete Comput. Geom. 41 365–375.Google Scholar
[2]Agarwal, P. K., Aronov, B., Pach, J., Pollack, R. and Sharir, M. (1997) Quasi-planar graphs have a linear number of edges. Combinatorica 17 1–9.CrossRefGoogle Scholar
[3]Ajtai, M., Chvátal, V., Newborn, M. and Szemerédi, E. (1982) Crossing-free subgraphs. In Theory and Practice of Combinatorics, Vol. 60 of Mathematics Studies, North-Holland, pp. 9–12.Google Scholar
[4]Biswal, P., Lee, J. R. and Rao, S. (2010) Eigenvalue bounds, spectral partitioning, and metrical deformations via flows. J. Assoc. Comput. Mach. 57 #13.Google Scholar
[5]Chudnovsky, M. (2013) The Erdős–Hajnal conjecture: A survey. J. Graph Theory, to appear.CrossRefGoogle Scholar
[6]Erdős, P. and Hajnal, A. (1989) Ramsey-type theorems. Discrete Appl. Math. 25 37–52.Google Scholar
[7]Feige, U., Hajiaghayi, M. T. and Lee, J. R. (2008) Improved approximation algorithms for minimum weight vertex separators. SIAM J. Comput. 38 629–657.Google Scholar
[8]Fox, J. (2006) A bipartite analogue of Dilworth's theorem. Order 23 197–209.Google Scholar
[9]Fox, J. and Pach, J. (2008) Separator theorems and Turán-type results for planar intersection graphs. Adv. Math. 219 1070–1080.Google Scholar
[10]Fox, J. and Pach, J. (2008) Erdős–Hajnal-type results on intersection patterns of geometric objects. In Horizons of Combinatorics, Vol. 17 of Bolyai Society Mathematical Studies, Springer, pp. 79–103.Google Scholar
[11]Fox, J. and Pach, J. (2010) A separator theorem for string graphs and its applications. Combin. Probab. Comput. 19 371–390.Google Scholar
[12]Fox, J. and Pach, J. (2012) String graphs and incomparability graphs. Adv. Math. 230 1381–1401.Google Scholar
[13]Fox, J. and Pach, J. (2012) Coloring Kk-free intersection graphs of geometric objects in the plane. Europ. J. Combin. 33 853–866.Google Scholar
[14]Fox, J., Pach, J. and Tóth, C. D. (2010) A bipartite strengthening of the crossing lemma. J. Combin. Theory Ser. B 100 23–35.Google Scholar
[15]Kővári, T., Sós, V. and Turán, P. (1954) On a problem of K. Zarankiewicz. Colloq. Math. 3 50–57.Google Scholar
[16]Leighton, T. (1984) New lower bound techniques for VLSI. Math. Systems Theory 17 47–70.Google Scholar
[17]Matoušek, J. (2013) Near-optimal separators in string graphs. Comb. Probab. Comput. doi. 10.1017/S0963548313000400.Google Scholar
[18]Pach, J. (1991) Notes on geometric graph theory. In Discrete and Computational Geometry (Goodman, J. E.et al., eds),Vol. 6 of DIMACS Series, AMS, pp. 273–285.Google Scholar
[19]Pach, J. and Sharir, M. (2009) On planar intersection graphs with forbidden subgraphs. J. Graph Theory 59 205–214.CrossRefGoogle Scholar
[20]Pach, J., Radoičić, R. and Tóth, G. (2003) Relaxing planarity for topological graphs. In Discrete and Computational Geometry (Akiyama, J. and Kano, M., eds), Vol. 2866 of Lecture Notes in Computer Science, Springer, pp. 221–232. Also in More Sets, Graphs and Numbers (2006), Vol. 15 of Bolyai Society Mathematical Studies 15, Springer, pp. 285–300.Google Scholar
[21]Pawlik, A., Kozik, J., Krawczyk, T., Lasoń, M., Micek, P., Trotter, W. T. and Walczak, B. (2012) Triangle-free intersection graphs of line segments with large chromatic number. Preprint. arXiv:1209.1595Google Scholar
[22]Radoičić, R. and Tóth, G. (2008) The discharging method in combinatorial geometry and the Pach–Sharir conjecture. In Surveys on Discrete and Computational Geometry, Vol. 453 of Contemporary Mathematics, AMS, pp. 319–342.Google Scholar