Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T23:12:07.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Corners Over Quasirandom Groups

Part of: Extremal combinatorics Representation theory of groups

Published online by Cambridge University Press:  06 June 2017

PAVEL ZORIN-KRANICH
PAVEL ZORIN-KRANICH*
Affiliation:
Mathematisches Institut, Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany (e-mail: pzorin@math.uni-bonn.de), http://www.math.uni-bonn.de/people/pzorin/
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite D-quasirandom group and A ⊂ Gk a δ-dense subset. Then the density of the set of side lengths g of corners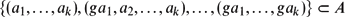

$$ \{(a_{1},\dotsc,a_{k}),(ga_{1},a_{2},\dotsc,a_{k}),\dotsc,(ga_{1},\dotsc,ga_{k})\} \subset A $$
converges to 1 as D → ∞.

MSC classification

Primary: 05D10: Ramsey theory
Secondary: 20D60: Arithmetic and combinatorial problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 6 , November 2017 , pp. 944 - 951
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M. and Szemerédi, E. (1974) Sets of lattice points that form no squares. Studia Sci. Math. Hungar. 9 9–11.Google Scholar
[2] Austin, T. (2015) Quantitative equidistribution for certain quadruples in quasi-random groups. Combin. Probab. Comput. 24 376–381. With erratum.Google Scholar
[3] Austin, T. (2016) Ajtai–Szemerédi theorems over quasirandom groups. In Recent Trends in Combinatorics, Vol. 159 of The IMA Volumes in Mathematics and its Applications, Springer, pp. 453–484.Google Scholar
[4] Austin, T. (2016) Non-conventional ergodic averages for several commuting actions of an amenable group. J. Analyse Math. 130 243–274. arXiv:1309.4315 Google Scholar
[5] Bergelson, V., McCutcheon, R. and Zhang, Q. (1997) A Roth theorem for amenable groups. Amer. J. Math. 119 1173–1211.Google Scholar
[6] Bergelson, V., Robertson, D. and Zorin-Kranich, P. (2017) Triangles in Cartesian squares of quasirandom groups. Combin. Probab. Comput. 26 161–182.Google Scholar
[7] Bergelson, V. and Tao, T. (2014) Multiple recurrence in quasirandom groups. Geom. Funct. Anal. 24 1–48.Google Scholar
[8] Furstenberg, H. (1977) Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Analyse Math. 31 204–256.Google Scholar
[9] Furstenberg, H. and Katznelson, Y. (1978) An ergodic Szemerédi theorem for commuting transformations. J. Analyse Math. 34 275–291.Google Scholar
[10] Gowers, W. T. (2007) Hypergraph regularity and the multidimensional Szemerédi theorem. Ann. of Math. (2) 166 897–946.CrossRefGoogle Scholar
[11] Gowers, W. T. (2008) Quasirandom groups. Combin. Probab. Comput. 17 363–387.Google Scholar
[12] Roth, K. F. (1953) On certain sets of integers. J. London Math. Soc. 28 104–109.Google Scholar
[13] Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 199–245.Google Scholar
[14] Tao, T. (2006) A variant of the hypergraph removal lemma. J. Combin. Theory Ser. A 113 1257–1280.Google Scholar
[15] Tao, T. (2007) The ergodic and combinatorial approaches to Szemerédi's theorem. In Additive Combinatorics, Vol. 43 of CRM Proc. Lecture Notes, AMS, pp. 145–193.CrossRefGoogle Scholar
[16] Tao, T. (2012) Higher Order Fourier Analysis, Vol. 142 of Graduate Studies in Mathematics, AMS.Google Scholar