Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T09:14:13.707Z Has data issue: false hasContentIssue false
  • English
  • Français

The Density Turán Problem

Published online by Cambridge University Press:  29 February 2012

PÉTER CSIKVÁRI  and
ZOLTÁN LÓRÁNT NAGY
PÉTER CSIKVÁRI
Affiliation:
Eötvös Loránd University, Department of Computer Science, H-1117 Budapest, Pázmány Péter sétány 1/C, Hungary and Alfréd Rényi Institute of Mathematics, H-1053 Budapest, Reáltanoda u. 13-15, Hungary (e-mail: csiki@cs.elte.hu, nagyzoltanlorant@gmail.com)
ZOLTÁN LÓRÁNT NAGY
Affiliation:
Eötvös Loránd University, Department of Computer Science, H-1117 Budapest, Pázmány Péter sétány 1/C, Hungary and Alfréd Rényi Institute of Mathematics, H-1053 Budapest, Reáltanoda u. 13-15, Hungary (e-mail: csiki@cs.elte.hu, nagyzoltanlorant@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be a graph on n vertices and let the blow-up graph G[H] be defined as follows. We replace each vertex vi of H by a cluster Ai and connect some pairs of vertices of Ai and Aj if (vi,vj) is an edge of the graph H. As usual, we define the edge density between Ai and Aj as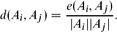 We study the following problem. Given densities γij for each edge (i,j) ∈ E(H), one has to decide whether there exists a blow-up graph G[H], with edge densities at least γij, such that one cannot choose a vertex from each cluster, so that the obtained graph is isomorphic to H, i.e., no H appears as a transversal in G[H]. We call dcrit(H) the maximal value for which there exists a blow-up graph G[H] with edge densities d(Ai,Aj)=dcrit(H) ((vi,vj) ∈ E(H)) not containing H in the above sense. Our main goal is to determine the critical edge density and to characterize the extremal graphs.

First, in the case of tree T we give an efficient algorithm to decide whether a given set of edge densities ensures the existence of a transversal T in the blow-up graph. Then we give general bounds on dcrit(H) in terms of the maximal degree. In connection with the extremal structure, the so-called star decomposition is proved to give the best construction for H-transversal-free blow-up graphs for several graph classes. Our approach applies algebraic graph-theoretical, combinatorial and probabilistic tools.

Keywords

Primary 05C3505C4205C31
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 4 , July 2012 , pp. 531 - 553
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Spencer, J. H. (2000) The Probabilistic Method, second edition, Wiley.CrossRefGoogle Scholar
[2]Bollobás, B. (1978) Extremal Graph Theory, Academic Press.Google Scholar
[3]Bollobás, B., Erdős, P. and Strauss, E. G. (1974) Complete subgraphs of chromatic graphs and hypergraphs. Utilitas Math. 6 343–347.Google Scholar
[4]Bollobás, B., Erdős, P. and Szemerédi, E. (1975) On complete subgraphs of r-chromatic graphs. Discrete Math. 13 97–107.CrossRefGoogle Scholar
[5]Bondy, A., Shen, J., Thomassé, S. and Thomassen, C. (2006) Density conditions for triangles in multipartite graphs. Combinatorica 26 121–131.CrossRefGoogle Scholar
[6]Csikvári, P. (2010) Integral trees of arbitrarily large diameters. J. Alg. Combin. 32 371–377.CrossRefGoogle Scholar
[7]Füredi, Z. (1991) Turán type problems. In Surveys in Combinatorics, Vol. 166 of London Math. Soc. Lecture Notes (Keedwell, A. D., ed.), pp. 253–300.Google Scholar
[8]Gács, A. private communication.Google Scholar
[9]Godsil, C. D. and Royle, G. (2001) Algebraic Graph Theory, Springer.CrossRefGoogle Scholar
[10]Jin, G. (1992) Complete subgraphs of r-partite graphs. Combin. Probab. Comput. 1 241–250.CrossRefGoogle Scholar
[11]Heilmann, O. J. and Lieb, E. H. (1972) Theory of monomer–dimer systems. Commun. Math. Phys. 25 190–232.CrossRefGoogle Scholar
[12]Nagy, Z. L. (2011) A multipartite version of the Turán problem: Density conditions and eigenvalues. Electron. J. Combin. 18 #46.CrossRefGoogle Scholar
[13]Scott, A. D. and Sokal, A. D. (2005) The repulsive lattice gas, the independent-set polynomial, and the Lovász local lemma. J. Statist. Phys. 118 1151–1261.CrossRefGoogle Scholar
[14]Talbot, J., Baber, R. and Johnson, J. R. (2010) The minimal density of triangles in tripartite graphs. LMS J. Comput. Math. 13 388–413.Google Scholar
[15]Turán, P. (1941) On an extremal problem in graph theory. Mat. Fiz. Lapok 48. 436–452.Google Scholar
[16]Yuster, R. (1997) Independent transversals in r-partite graphs. Discrete Math. 176 255–261.CrossRefGoogle Scholar