Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhai, Mingqing
and
Lin, Huiqiu
2020.
Spectral extrema of graphs: Forbidden hexagon.
Discrete Mathematics,
Vol. 343,
Issue. 10,
p.
112028.
Duan, Xiuzhuan
Ning, Bo
Peng, Xing
Wang, Jian
and
Yang, Weihua
2020.
Maximizing the number of cliques in graphs with given matching number.
Discrete Applied Mathematics,
Vol. 287,
Issue. ,
p.
110.
Guo, Hangtian
Lin, Huiqiu
and
Zhao, Yanhua
2021.
A spectral condition for the existence of a pentagon in non-bipartite graphs.
Linear Algebra and its Applications,
Vol. 627,
Issue. ,
p.
140.
Lin, Huiqiu
and
Guo, Hangtian
2021.
A spectral condition for odd cycles in non-bipartite graphs.
Linear Algebra and its Applications,
Vol. 631,
Issue. ,
p.
83.
Zhai, Mingqing
Lin, Huiqiu
and
Shu, Jinlong
2021.
Spectral extrema of graphs with fixed size: Cycles and complete bipartite graphs.
European Journal of Combinatorics,
Vol. 95,
Issue. ,
p.
103322.
Zhu, Xiutao
Zhang, Fangfang
and
Chen, Yaojun
2021.
Generalized Turán Number of Even Linear Forests.
Graphs and Combinatorics,
Vol. 37,
Issue. 4,
p.
1437.
Zhai, Mingqing
and
Lin, Huiqiu
2022.
Spectral extrema of K,-minor free graphs – On a conjecture of M. Tait.
Journal of Combinatorial Theory, Series B,
Vol. 157,
Issue. ,
p.
184.
Zhang, Lin-Peng
Wang, Ligong
and
Zhou, Jiale
2022.
The Generalized Turán Number of Spanning Linear Forests.
Graphs and Combinatorics,
Vol. 38,
Issue. 2,
Zhu, Xiutao
and
Chen, Yaojun
2022.
Generalized Turán number for linear forests.
Discrete Mathematics,
Vol. 345,
Issue. 10,
p.
112997.
Zhang, Zhiyuan
and
Zhao, Yanhua
2023.
A spectral condition for the existence of cycles with consecutive odd lengths in non-bipartite graphs.
Discrete Mathematics,
Vol. 346,
Issue. 6,
p.
113365.
Zhang, Leilei
2023.
Further Results on the Generalized Turán Number of Spanning Linear Forests.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 1,
Fu, Miao
and
Zhang, Yuqin
2023.
Results on monochromatic vertex disconnection of graphs.
AIMS Mathematics,
Vol. 8,
Issue. 6,
p.
13219.
Hu, Yarong
Lou, Zhenzhen
and
Huang, Qiongxiang
2023.
Ordering Q-indices of graphs: Given size and circumference.
Discrete Mathematics,
Vol. 346,
Issue. 12,
p.
113628.
Zhai, Mingqing
and
Lin, Huiqiu
2023.
A strengthening of the spectral chromatic critical edge theorem: Books and theta graphs.
Journal of Graph Theory,
Vol. 102,
Issue. 3,
p.
502.
Li, Binlong
and
Ning, Bo
2023.
Eigenvalues and cycles of consecutive lengths.
Journal of Graph Theory,
Vol. 103,
Issue. 3,
p.
486.
Zhang, Leilei
2023.
The maximum number of cliques in graphs with prescribed order, circumference and minimum degree.
European Journal of Combinatorics,
Vol. 112,
Issue. ,
p.
103728.
Lv, Zequn
Győri, Ervin
He, Zhen
Salia, Nika
Xiao, Chuanqi
and
Zhu, Xiutao
2024.
The Maximum Number of Cliques in Graphs with Bounded Odd Circumference.
Annals of Combinatorics,
Vol. 28,
Issue. 4,
p.
1119.
Zhang, Wenqian
2024.
The Spectral Radius, Maximum Average Degree and Cycles of Consecutive Lengths of Graphs.
Graphs and Combinatorics,
Vol. 40,
Issue. 2,
Liu, Yuxuan
and
Zhang, Leilei
2024.
The maximum number of complete multipartite subgraphs in graphs with given circumference or matching number.
Discrete Mathematics,
Vol. 347,
Issue. 1,
p.
113734.
An, Yonghong
and
Zhang, Guizhi
2024.
Sufficient conditions for k-connected graphs and k-leaf-connected graphs.
Filomat,
Vol. 38,
Issue. 18,
p.
6601.
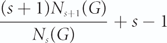 $${{(s + 1){N_{s + 1}}(G)} \over {{N_s}(G)}} + s - 1$$
$${{(s + 1){N_{s + 1}}(G)} \over {{N_s}(G)}} + s - 1$$
