Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T23:42:42.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Frozen (Δ + 1)-colourings of bounded degree graphs

Part of: Graph theory

Published online by Cambridge University Press:  19 October 2020

Marthe Bonamy ,
Nicolas Bousquet  and
Guillem Perarnau
Marthe Bonamy
Affiliation:
CNRS, LaBRI, Université de Bordeaux, France
Nicolas Bousquet
Affiliation:
LIRIS, CNRS, Université Claude Bernard Lyon 1, Lyon, France
Guillem Perarnau*
Affiliation:
Departament de Matemàtiques (MAT), Universitat Politècnica de Catalunya (UPC), Barcelona, Spain
*
*Corresponding author. Email: guillem.perarnau@upc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a graph on n vertices and with maximum degree Δ, and let k be an integer. The k-recolouring graph of G is the graph whose vertices are k-colourings of G and where two k-colourings are adjacent if they differ at exactly one vertex. It is well known that the k-recolouring graph is connected for 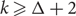$k\geq \Delta+2$ . Feghali, Johnson and Paulusma (J. Graph Theory83 (2016) 340–358) showed that the (Δ + 1)-recolouring graph is composed by a unique connected component of size at least 2 and (possibly many) isolated vertices.

In this paper, we study the proportion of isolated vertices (also called frozen colourings) in the (Δ + 1)-recolouring graph. Our first contribution is to show that if G is connected, the proportion of frozen colourings of G is exponentially smaller in n than the total number of colourings. This motivates the use of the Glauber dynamics to approximate the number of (Δ + 1)-colourings of a graph. In contrast to the conjectured mixing time of O(nlog n) for 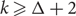$k\geq \Delta+2$ colours, we show that the mixing time of the Glauber dynamics for (Δ + 1)-colourings restricted to non-frozen colourings can be Ω(n2). Finally, we prove some results about the existence of graphs with large girth and frozen colourings, and study frozen colourings in random regular graphs.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 330 - 343
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, E. A. (1974) The asymptotic number of non-negative integer matrices with given row and column sums. Discrete Math. 10 217–223.Google Scholar
Bonamy, M. and Bousquet, N. (2014) Reconfiguring independent sets in cographs. CoRR.Google Scholar
Bonsma, P., Mouawad, A., Nishimura, N. and Raman, V. (2014) The complexity of bounded length graph recoloring and CSP reconfiguration. In Parameterized and Exact Computation (IPEC), Vol. 8894 of Lecture Notes in Computer Science, pp. 110–121, Springer.Google Scholar
Chen, S., Delcourt, M., Moitra, A., Perarnau, G. and Postle, L. (2019) Improved bounds for randomly sampling colorings via linear programming. In Thirtieth Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 2216–2234, SIAM.CrossRefGoogle Scholar
Diestel, R. (2005) Graph Theory, third edition, Vol. 173 of Graduate Texts in Mathematics, Springer.Google Scholar
Dyer, M., Goldberg, L. and Jerrum, M. (2006) Systematic scan for sampling colorings. Ann. Appl. Probab. 16 185–230.CrossRefGoogle Scholar
Feghali, C., Johnson, M. and Paulusma, D. (2016) A reconfigurations analogue of Brooks’ theorem and its consequences. J. Graph Theory 83 340–358.Google Scholar
Feghali, C., Johnson, M. and Paulusma, D. (2017) Kempe equivalence of colourings of cubic graphs. European J. Combin. 59 1–10.CrossRefGoogle Scholar
Fortin, J. and Rudinsky, S. (2013) Asymptotic eigenvalue distribution of random lifts. Waterloo Math. Review 2 20–28.Google Scholar
Gopalan, P., Kolaitis, P., Maneva, E. and Papadimitriou, C. (2009) The connectivity of Boolean satisfiability: computational and structural dichotomies. SIAM J. Comput. 38 2330–2355.CrossRefGoogle Scholar
Hayes, T. P. and Sinclair, A. (2005) A general lower bound for mixing of single-site dynamics on graphs. In 46th Annual IEEE Symposium on Foundations of Computer Science 2005 (FOCS 2005), pp. 511–520, IEEE.Google Scholar
Ito, T., Demaine, E., Harvey, N., Papadimitriou, C., Sideri, M., Uehara, R. and Uno, Y. (2011) On the complexity of reconfiguration problems. Theoret. Comput. Sci. 412 1054–1065.Google Scholar
Ito., T., Kaminski, M. and Ono, H. (2014) Independent set reconfiguration in graphs without large bicliques. In ISAAC’14.Google Scholar
Janson, S. (2018) Tail bounds for sums of geometric and exponential variables. Stat Probab Lett. 135 1–6.CrossRefGoogle Scholar
Jerrum, M. (1995) A very simple algorithm for estimating the number of k-colorings of a low-degree graph. Random Struct. Algorithms 7 157–165.CrossRefGoogle Scholar
Jerrum, M., Valiant, L. G. and Vazirani, V. (1986) Random generation of combinatorial structures from a uniform distribution. Theoret. Comput. Sci. 43 169–188.CrossRefGoogle Scholar
Lu, P., Yang, K., Zhang, C. and Zhu, M. (2017) An FPTAS for counting proper four-colorings on cubic graphs. In Twenty-Eighth Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 1798–1817, SIAM.CrossRefGoogle Scholar
Martinelli, F. (1999) Lectures on Glauber Dynamics for Discrete Spin Models, Springer.CrossRefGoogle Scholar
Salas, J. and Sokal, A. D. (1997) Absence of phase transition for antiferromagnetic Potts models via the Dobrushin uniqueness theorem. J. Statist. Phys. 86 551–579.Google Scholar
Suzuki, A., Mouawad, A. and Nishimura, N. (2016) Reconfiguration of dominating sets. J. Comb. Optim. 32 1182–1195.Google Scholar
van den Heuvel, J. (2013) The Complexity of Change (Blackburn, S. R., Gerke, S. and Wildon, M., eds), Vol. 409 of London Mathematical Society Lecture Note Series, Cambridge University Press.Google Scholar
Vigoda, E. (2000) Improved bounds for sampling colorings. J. Math. Phys. 41 1555–1569.CrossRefGoogle Scholar