Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T23:44:09.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Hamiltonicity in random directed graphs is born resilient

Part of: Graph theory

Published online by Cambridge University Press:  24 June 2020

Richard Montgomery
Richard Montgomery*
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
*
Email: r.h.montgomery@bham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 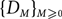$\{D_M\}_{M\geq 0}$ be the n-vertex random directed graph process, where 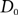$D_0$ is the empty directed graph on n vertices, and subsequent directed graphs in the sequence are obtained by the addition of a new directed edge uniformly at random. For each 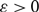$$\varepsilon > 0$$ , we show that, almost surely, any directed graph 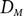$D_M$ with minimum in- and out-degree at least 1 is not only Hamiltonian (as shown by Frieze), but remains Hamiltonian when edges are removed, as long as at most 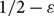$1/2-\varepsilon$ of both the in- and out-edges incident to each vertex are removed. We say such a directed graph is 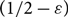$(1/2-\varepsilon)$ -resiliently Hamiltonian. Furthermore, for each 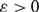$\varepsilon > 0$ , we show that, almost surely, each directed graph 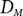$D_M$ in the sequence is not 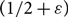$(1/2+\varepsilon)$ -resiliently Hamiltonian.

This improves a result of Ferber, Nenadov, Noever, Peter and Škorić who showed, for each 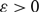$\varepsilon > 0$ , that the binomial random directed graph 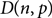$D(n,p)$ is almost surely 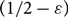$(1/2-\varepsilon)$ -resiliently Hamiltonian if 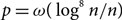$p=\omega(\log^8n/n)$ .

MSC classification

Primary: 05C20: Directed graphs (digraphs), tournaments
Secondary: 05C80: Random graphs 05C38: Paths and cycles 05C45: Eulerian and Hamiltonian graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 6 , November 2020 , pp. 900 - 942
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M., Komlós, J. and Szemerédi, E. (1985) First occurrence of Hamilton cycles in random graphs. North-Holland Math. Studies 115 173–178.CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B. (2007) Embedding nearly-spanning bounded degree trees. Combinatorica 27 629–644.CrossRefGoogle Scholar
Bal, D., Bennett, P., Cooper, C., Frieze, A. and Prałat, P. (2016) Rainbow arborescence in random digraphs. J. Graph Theory 83 251–265.CrossRefGoogle Scholar
Balogh, J., Csaba, B. and Samotij, W. (2011) Local resilience of almost spanning trees in random graphs. Random Struct. Algorithms 38 121–139.CrossRefGoogle Scholar
Ben-Shimon, S., Krivelevich, M. and Sudakov, B. (2011) On the resilience of Hamiltonicity and optimal packing of Hamilton cycles in random graphs. SIAM J. Discrete Math. 25 1176–1193.CrossRefGoogle Scholar
Bollobás, B. (1983) Almost all regular graphs are Hamiltonian. European J. Combin. 4 97–106.CrossRefGoogle Scholar
Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics: Cambridge Combinatorial Conference in Honour of Paul Erdös, pp. 335–357, Academic Press.Google Scholar
Dirac, G. (1952) Some theorems on abstract graphs. Proc. London Math. Soc. 3 69–81.Google Scholar
Erdös, P. and Rényi, A. (1959) On random graphs I. Publ. Math. Debrecen 6 290–297.Google Scholar
Erdös, P. and Rényi, A. (1964) On random matrices. Magyar Tud. Akad. Mat. Kutató Int. Közl 8 455–461.Google Scholar
Ferber, A., Nenadov, R., Noever, A., Peter, U. and Škorić, N. (2017) Robust Hamiltonicity of random directed graphs. J. Combin. Theory Ser. B 126 1–23.CrossRefGoogle Scholar
Frieze, A. (1988) An algorithm for finding Hamilton cycles in random directed graphs. J. Algorithms 9 181–204.CrossRefGoogle Scholar
Frieze, A. and Krivelevich, M. (2008) On two Hamilton cycle problems in random graphs. Israel J. Math. 166 221–234.CrossRefGoogle Scholar
Ghouila-Houri, A. (1960) Une condition suffisante d’existence d’un circuit Hamiltonien. CR Acad. Sci. Paris 251 495–497.Google Scholar
Glebov, R. (2013) On Hamilton cycles and other spanning structures. PhD thesis.Google Scholar
Hefetz, D., Krivelevich, M. and Szabó, T. (2012) Sharp threshold for the appearance of certain spanning trees in random graphs. Random Struct. Algorithms 41 391–412.CrossRefGoogle Scholar
Hefetz, D., Steger, A. and Sudakov, B. (2016) Random directed graphs are robustly Hamiltonian. Random Struct. Algorithms 49 345–362.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2011) Random Graphs, Wiley.Google Scholar
Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.CrossRefGoogle Scholar
Korshunov, A. (1976) Solution of a problem of Erdös and Rényi on Hamilton cycles in non-oriented graphs. Soviet Math. Dokl. 17 760–764.Google Scholar
Krivelevich, M., Lee, C. and Sudakov, B. (2010) Resilient pancyclicity of random and pseudorandom graphs. SIAM J. Discrete Math. 24 1–16.CrossRefGoogle Scholar
Lee, C. and Sudakov, B. (2012) Dirac’s theorem for random graphs. Random Struct. Algorithms 41 293–305.CrossRefGoogle Scholar
McDiarmid, C. (1983) General first-passage percolation. Adv. Appl. Probab. 15 149–161.CrossRefGoogle Scholar
Montgomery, R. (2019) Hamiltonicity in random graphs is born resilient. J. Comb. Theory Ser. B. 139 316–341.CrossRefGoogle Scholar
Nenadov, R., Steger, A. and Trujić, M. Resilience of perfect matchings and Hamiltonicity in random graph processes. Random Struct. Algorithms, 54 797–819.CrossRefGoogle Scholar
Pittel, B. (1982) On the probable behaviour of some algorithms for finding the stability number of a graph. Math. Proc. Cambridge Philos. Soc. 92 511–526.Google Scholar
Pósa, L. (1976) Hamiltonian circuits in random graphs. Discrete Math. 14 359–364.CrossRefGoogle Scholar
Rödl, V., Szemerédi, E. and Ruciński, A. (2008) An approximate Dirac-type theorem for k-uniform hypergraphs. Combinatorica 28 229–260.CrossRefGoogle Scholar
Spencer, J. (1977) Asymptotic lower bounds for Ramsey functions. Discrete Math. 20 69–76.CrossRefGoogle Scholar
Sudakov, B. (2017) Robustness of graph properties. In Surveys in Combinatorics 2017, Vol. 440 of London Mathematical Society Lecture Note Series, pp. 372–408, Cambridge University Press.Google Scholar
Sudakov, B. and Vu, V. (2008) Local resilience of graphs. Random Struct. Algorithms 33 409–433.CrossRefGoogle Scholar