Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T05:45:59.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant Measure Under the Affine Group Over 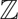${\mathbb{Z}$

Published online by Cambridge University Press:  02 January 2014

DANIELE MUNDICI
DANIELE MUNDICI*
Affiliation:
Department of Mathematics and Computer Science, University of Florence, Viale Morgagni 67/A, 50134 Florence, Italy (e-mail: mundici@math.unifi.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

A rational polyhedron$P\subseteq {\mathbb{R^n}}$ is a finite union of simplexes in ${\mathbb{R^n}}$ with rational vertices. P is said to be $\mathbb Z$-homeomorphic to the rational polyhedron 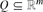$Q\subseteq {\mathbb{R^{\it m}}}$ if there is a piecewise linear homeomorphism η of P onto Q such that each linear piece of η and η−1 has integer coefficients. When n=m, $\mathbb Z$-homeomorphism amounts to continuous 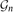$\mathcal{G}_n$-equidissectability, where 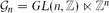$\mathcal{G}_n=GL(n,\mathbb Z) \ltimes \mathbb Z^{n}$ is the affine group over the integers, i.e., the group of all affinities on $\mathbb{R^{n}}$ that leave the lattice $\mathbb Z^{n}$ invariant. 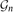$\mathcal{G}_n$ yields a geometry on the set of rational polyhedra. For each d=0,1,2,. . ., we define a rational measure λd on the set of rational polyhedra, and show that any two $\mathbb Z$-homeomorphic rational polyhedra $$P\subseteq {\mathbb{R^n}}$$ and 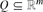$Q\subseteq {\mathbb{R^{\it m}}}$ satisfy 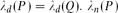$\lambda_d(P)=\lambda_d(Q)$. $\lambda_n(P)$ coincides with the n-dimensional Lebesgue measure of P. If 0 ≤ dim P=d < n then λd(P)>0. For rational d-simplexes T lying in the same d-dimensional affine subspace of 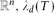${\mathbb{R^{\it n}}, $\lambda_d(T)$$ is proportional to the d-dimensional Hausdorff measure of T. We characterize λd among all unimodular invariant valuations.

Keywords

Primary 20H25Secondary 20H0551M2551N2552B2014E0552A38
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 2 , March 2014 , pp. 248 - 268
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Barvinok, A. (2002) A Course in Convexity, Vol. 54 of Graduate Studies in Mathematics, AMS.Google Scholar
[2]Betke, U. and Kneser, M. (1985) Zerlegungen und Bewertungen von Gitterpolytopen. J. Reine Angew. Math. 358 202–208.Google Scholar
[3]Birkhoff, G. and Mac Lane, S. (1953) A Survey of Modern Algebra, revised edition, Macmillan.Google Scholar
[4]Boca, F. (2008) An AF algebra associated with the Farey tessellation. Canad. J. Math. 60 975–1000.Google Scholar
[5]Dani, S. G. (1979) On invariant measures, minimal sets and a lemma of Margulis. Inventio. Math. 51 239–260.CrossRefGoogle Scholar
[6]Danilov, V. I. (1983) Birational geometry of toric 3-folds. Math. USSR Izvestiya 21 269–280.Google Scholar
[7]Ehrhart, E. (1962) Sur les polyèdres rationnels homothétiques à n dimensions. CR Acad. Sci. Paris Sér. A 254 616–618.Google Scholar
[8]Ewald, G. (1996) Combinatorial Convexity and Algebraic Geometry, Springer.Google Scholar
[9]Federer, H. (1969) Geometric Measure Theory, Springer.Google Scholar
[10]Fremlin, D. H. (2011) Measure Theory, Vol. 1, second edition. First published in 2000 by Torres Fremlin, 25 Ireton Road, Colchester CO3 3AT, UK. Source files available from: http://www.essex.ac.uk/maths/people/fremlin/mt1.2011/index.htmGoogle Scholar
[11]Glass, A. M. W. and Madden, J. J. (1984) The word problem versus the isomorphism problem. J. London Math. Soc. (2) 30 53–61.CrossRefGoogle Scholar
[12]Gruber, P. M. (2007) Convex and Discrete Geometry, Vol. 336 of Grundlehren der Mathematischen Wissenschaften, Springer.Google Scholar
[13]Lekkerkerker, C. G. (1969) Geometry of Numbers, Wolters-Noordhoff.Google Scholar
[14]McMullen, P. (1993) Valuations and dissections. In Handbook of Convex Geometry, Vol. 2 (Gruber, P. M. and Wills, J. M., eds), Elsevier, pp. 933–988.Google Scholar
[15]Morelli, R. (1996) The birational geometry of toric varieties. J. Algebraic Geometry 5 751–782.Google Scholar
[16]Mundici, D. (1988) Farey stellar subdivisions, ultrasimplicial groups, and K 0 of AF C*-algebras. Adv. Math. 68 23–39.Google Scholar
[17]Mundici, D. (2008) The Haar theorem for lattice-ordered abelian groups with order-unit. Discrete Continuous Dyn. Syst. 21 537–549.CrossRefGoogle Scholar
[18]Mundici, D. (2011) Finite axiomatizability in Ł ukasiewicz logic. Ann. Pure Applied Logic 162 1035–1047.CrossRefGoogle Scholar
[19]Mundici, D. (2011) Revisiting the Farey AF algebra. Milan J. Math. 79 643–656.CrossRefGoogle Scholar
[20]Nogueira, A. (2002) Relatively prime numbers and invariant measures under the natural action of $SL(n,\mathbb Z)$ on ${\mathbb{R^n}}$. Ergodic Theory Dyn. Syst. 22 899–923.Google Scholar
[21]Oda, T. (1988) Convex Bodies and Algebraic Geometry: An Introduction to the Theory of Toric Varieties, Springer.Google Scholar
[22]Panti, G. (2009) Invariant measures in free MV-algebras. Commun. Algebra 36 2849–2861.Google Scholar
[23]Panti, G. (2012) Denominator-preserving maps. Aequationes Math. 84 13–25.Google Scholar
[24]Semadeni, Z. (1982) Schauder Bases in Banach Spaces of Continuous Functions, Vol. 918 of Lecture Notes in Mathematics, Springer.CrossRefGoogle Scholar
[25]Shtan'ko, M. A. (2004) Markov's theorem and algorithmically non-recognizable combinatorial manifolds. Izvestiya RAN, Ser. Math. 68 207–224.Google Scholar
[26]Stallings, J. R. (1968) Lectures on Polyhedral Topology, Vol. 43 of Lectures in Mathematics, Tata Institute of Fundamental Research.Google Scholar
[27]Włodarczyk, J. (1997) Decompositions of birational toric maps in blow-ups and blow-downs. Trans. Amer. Math. Soc. 349 373–411.CrossRefGoogle Scholar