Article contents
Many Turán exponents via subdivisions
Published online by Cambridge University Press: 21 July 2022
Abstract
Given a graph 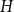 $H$ and a positive integer
$H$ and a positive integer  $n$, the Turán number
$n$, the Turán number 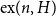 $\mathrm{ex}(n,H)$ is the maximum number of edges in an
$\mathrm{ex}(n,H)$ is the maximum number of edges in an  $n$-vertex graph that does not contain
$n$-vertex graph that does not contain 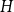 $H$ as a subgraph. A real number
$H$ as a subgraph. A real number 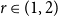 $r\in (1,2)$ is called a Turán exponent if there exists a bipartite graph
$r\in (1,2)$ is called a Turán exponent if there exists a bipartite graph 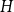 $H$ such that
$H$ such that 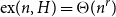 $\mathrm{ex}(n,H)=\Theta (n^r)$. A long-standing conjecture of Erdős and Simonovits states that
$\mathrm{ex}(n,H)=\Theta (n^r)$. A long-standing conjecture of Erdős and Simonovits states that 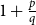 $1+\frac{p}{q}$ is a Turán exponent for all positive integers
$1+\frac{p}{q}$ is a Turán exponent for all positive integers 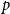 $p$ and
$p$ and 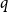 $q$ with
$q$ with 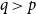 $q\gt p$.
$q\gt p$.
In this paper, we show that 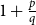 $1+\frac{p}{q}$ is a Turán exponent for all positive integers
$1+\frac{p}{q}$ is a Turán exponent for all positive integers 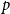 $p$ and
$p$ and 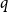 $q$ with
$q$ with 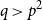 $q \gt p^{2}$. Our result also addresses a conjecture of Janzer [18].
$q \gt p^{2}$. Our result also addresses a conjecture of Janzer [18].
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Research supported in part by NSF grant DMS-1855542.
Research supported in part by China Scholarship Council grant #201806340156.
References
- 3
- Cited by


