Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-11T04:55:09.396Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone Cellular Automata in a Random Environment

Part of: Combinatorial probability Special processes

Published online by Cambridge University Press:  02 February 2015

BÉLA BOLLOBÁS ,
PAUL SMITH  and
ANDREW UZZELL
BÉLA BOLLOBÁS
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Wilberforce Road, Cambridge, CB3 0WA, UK; Department of Mathematical Sciences, University of Memphis, Memphis, TN 38152, USA; London Institute for Mathematical Sciences, 35a South Street, London, W1K 2XF, UK (e-mail: b.bollobas@dpmms.cam.ac.uk)
PAUL SMITH
Affiliation:
IMPA, 110 Estrada Dona Castorina, Jardim Botânico, Rio de Janeiro, 22460-320, Brazil (e-mail: psmith@impa.br)
ANDREW UZZELL
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden (e-mail: andrew.uzzell@math.uu.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study in complete generality the family of two-state, deterministic, monotone, local, homogeneous cellular automata in $\mathbb{Z}$d with random initial configurations. Formally, we are given a set 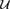$\mathcal{U}$ = {X1,. . . , Xm} of finite subsets of $\mathbb{Z}$d \ {0}, and an initial set A0 ⊂ $\mathbb{Z}$d of ‘infected’ sites, which we take to be random according to the product measure with density p. At time t ∈ $\mathbb{N}$, the set of infected sites At is the union of At-1 and the set of all x ∈ $\mathbb{Z}$d such that x + X ∈ At-1 for some X ∈ 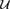$\mathcal{U}$. Our model may alternatively be thought of as bootstrap percolation on $\mathbb{Z}$d with arbitrary update rules, and for this reason we call it 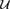$\mathcal{U}$-bootstrap percolation.

In two dimensions, we give a classification of 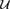$\mathcal{U}$-bootstrap percolation models into three classes – supercritical, critical and subcritical – and we prove results about the phase transitions of all models belonging to the first two of these classes. More precisely, we show that the critical probability for percolation on ($\mathbb{Z}$/n$\mathbb{Z}$)2 is (log n)−Θ(1) for all models in the critical class, and that it is n−Θ(1) for all models in the supercritical class.

The results in this paper are the first of any kind on bootstrap percolation considered in this level of generality, and in particular they are the first that make no assumptions of symmetry. It is the hope of the authors that this work will initiate a new, unified theory of bootstrap percolation on $\mathbb{Z}$d.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Special Issue 4: Oberwolfach Special Issue Part 1 , July 2015 , pp. 687 - 722
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aizenman, M. and Lebowitz, J. L. (1988) Metastability effects in bootstrap percolation. J. Phys. A 21 3801–3813.CrossRefGoogle Scholar
[2]Balister, P., Bollobás, B., Przykucki, M. J. and Smith, P. J. Subcritical $\mathcal{U}$-bootstrap percolation models have non-trivial phase transitions. Trans. Amer. Math. Soc. In press. arXiv:1311.5883Google Scholar
[3]Balogh, J. and Bollobás, B. (2006) Bootstrap percolation on the hypercube. Probab. Theory Rel. Fields 134 624–648.CrossRefGoogle Scholar
[4]Balogh, J., Bollobás, B., Duminil-Copin, H. and Morris, R. (2012) The sharp threshold for bootstrap percolation in all dimensions. Trans. Amer. Math. Soc. 364 2667–2701.CrossRefGoogle Scholar
[5]Balogh, J., Bollobás, B. and Morris, R. (2009) Bootstrap percolation in three dimensions. Ann. Probab. 37 1329–1380.CrossRefGoogle Scholar
[6]Balogh, J., Bollobás, B. and Morris, R. (2009) Majority bootstrap percolation on the hypercube. Combin. Probab. Comput. 18 17–51.CrossRefGoogle Scholar
[7]Balogh, J., Peres, Y. and Pete, G. (2006) Bootstrap percolation on infinite trees and non-amenable groups. Combin. Probab. Comput. 15 715–730.CrossRefGoogle Scholar
[8]Biskup, M. and Schonmann, R. H. (2009) Metastable behavior for bootstrap percolation on regular trees. J. Statist. Phys. 136 667–676.CrossRefGoogle Scholar
[9]Cerf, R. and Cirillo, E. N. M. (1999) Finite size scaling in three-dimensional bootstrap percolation. Ann. Probab. 27 1837–1850.CrossRefGoogle Scholar
[10]Cerf, R. and Manzo, F. (2002) The threshold regime of finite volume bootstrap percolation. Stochastic Process. Appl. 101 69–82.CrossRefGoogle Scholar
[11]Chalupa, J., Leath, P. L. and Reich, G. R. (1979) Bootstrap percolation on a Bethe lattice. J. Phys. C 12 L31–L35.CrossRefGoogle Scholar
[12]Duarte, A. M. S. (1989) Simulation of a cellular automaton with an oriented bootstrap rule. Physica A 157 1075–1079.CrossRefGoogle Scholar
[13]Gravner, J. and Griffeath, D. (1996) First passage time for threshold growth dynamics on $\mathbb{Z}$2. Ann. Probab. 24 1752–1778.CrossRefGoogle Scholar
[14]Gravner, J. and Griffeath, D. (1999) Scaling laws for a class of critical cellular automaton growth rules. In Proc. Erdős Center Workshop on Random Walks, pp. 167–188.Google Scholar
[15]Holroyd, A. E. (2003) Sharp metastability threshold for two-dimensional bootstrap percolation. Probab. Theory Rel. Fields 125 195–224.CrossRefGoogle Scholar
[16]Mountford, T. S. (1995) Critical length for semi-oriented bootstrap percolation. Stochastic Process. Appl. 56 185–205.CrossRefGoogle Scholar
[17]Schonmann, R. H. (1990) Finite size scaling behavior of a biased majority rule cellular automaton. Physica A 167 619–627.CrossRefGoogle Scholar
[18]Schonmann, R. H. (1992) On the behavior of some cellular automata related to bootstrap percolation. Ann. Probab. 20 174–193.CrossRefGoogle Scholar
[19]Ulam, S. (1950) Random processes and transformations. In Proc. Internat. Congr. Math., pp. 264–275.Google Scholar
[20]van Enter, A. C. D. (1987) Proof of Straley's argument for bootstrap percolation. J. Statist. Phys. 48 943–945.CrossRefGoogle Scholar
[21]van Enter, A. C. D. and Hulshof, W. J. T.(2007) Finite-size effects for anisotropic bootstrap percolation: logarithmic corrections. J. Statist. Phys. 28 1383–1389.CrossRefGoogle Scholar
[22]von Neumann, J. (1966) Theory of Self-Reproducing Automata, University of Illinois Press.Google Scholar