Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T09:34:39.126Z Has data issue: false hasContentIssue false
  • English
  • Français

On Erdős–Ko–Rado for random hypergraphs I

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  25 June 2019

A. Hamm  and
J. Kahn
A. Hamm
Affiliation:
Department of Mathematics, Winthrop University, Rock Hill, SC 29733, USA
J. Kahn*
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ 08854, USA
*
*Corresponding author. Email: jkahn@math.rutgers.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A family of sets is intersecting if no two of its members are disjoint, and has the Erdős–Ko–Rado property (or is EKR) if each of its largest intersecting subfamilies has non-empty intersection.

Denote by 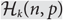${{\cal H}_k}(n,p)$ the random family in which each k-subset of {1, …, n} is present with probability p, independent of other choices. A question first studied by Balogh, Bohman and Mubayi asks:

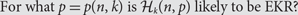\begin{equation} {\rm{For what }}p = p(n,k){\rm{is}}{{\cal H}_k}(n,p){\rm{likely to be EKR}}? \end{equation}

Here, for fixed c < 1/4, and $k \lt \sqrt {cn\log n} $ we give a precise answer to this question, characterizing those sequences p = p(n, k) for which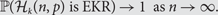

\begin{equation} {\mathbb{P}}({{\cal H}_k}(n,p){\rm{is EKR}}{\kern 1pt} ) \to 1{\rm{as }}n \to \infty . \end{equation}

MSC classification

Primary: 05D40: Probabilistic methods
Secondary: 05D05: Extremal set theory 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 6 , November 2019 , pp. 881 - 916
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by NSF grant DMS1201337.

References

Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, Wiley.CrossRefGoogle Scholar
Babai, L., Simonovits, M. and Spencer, J. (1990) Extremal subgraphs of random graphs. J. Graph Theory 14 599–622.CrossRefGoogle Scholar
Balogh, J., Bohman, T. and Mubayi, D. (2009) Erdős–Ko–Rado in random hypergraphs. Combin. Probab. Comput. 18 629–646.CrossRefGoogle Scholar
Balogh, J., Das, S., Delcourt, M., Liu, H. and Sharifzadeh, M. (2015) The typical structure of intersecting families of discrete structures. J. Combin. Theory Ser. A 132 224–245.CrossRefGoogle Scholar
Conlon, D. and Gowers, T. (2016) Combinatorial theorems in sparse random sets. Ann. of Math. 184 367–454.CrossRefGoogle Scholar
DeMarco, R. and Kahn, J. (2015) Mantel’s theorem for random graphs. Random Struct. Alg. 47 59–72.CrossRefGoogle Scholar
DeMarco, R. and Kahn, J. (2015) Turán’s theorem for random graphs. arXiv:1501.01340Google Scholar
Dubhashi, D. and Ranjan, D. (1998) Balls and bins: A study in negative dependence. Random Struct. Alg. 13 99–124.3.0.CO;2-M>CrossRefGoogle Scholar
Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford (2) 12 313–320.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Publ. Math. Inst. Hungar. Acad. Sci. 5 17–61.Google Scholar
Frankl, P. and Rödl, V. (1986) Large triangle-free subgraphs in graphs without K4. Graphs Combin. 2 135–144.CrossRefGoogle Scholar
Hamm, A. and Kahn, J. (2014) On Erdős–Ko–Rado for random hypergraphs II. Combin. Probab. Comput. 28 61–80.CrossRefGoogle Scholar
Harris, T. E. (1960) A lower bound on the critical probability in a certain percolation process. Proc. Cam. Phil. Soc.56 13–20.CrossRefGoogle Scholar
Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. (2) 18 369–384.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.CrossRefGoogle Scholar
Kahn, J. and Kalai, G. (2007) Thresholds and expectation thresholds. Combin. Probab. Comput. 16 495–502.CrossRefGoogle Scholar
Kohayakawa, Y., Łuczak, T. and Rödl, V. (1997) On K 4-free subgraphs of random graphs. Combinatorica 17 173–213.CrossRefGoogle Scholar
Pemantle, R. (2000) Towards a theory of negative dependence. J. Math. Phys. 41 1371–1390.CrossRefGoogle Scholar
Ramsey, F. B. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A. (1995) Threshold functions for Ramsey properties. J. Amer. Math. Soc. 8 917–942.CrossRefGoogle Scholar
Rödl, V. and Schacht, M. (2013) Extremal results in random graphs (English summary). In Erdős Centennial, Vol. 25 of Bolyai Society Mathematical Studies, János Bolyai Mathematical Society, pp. 535–583.Google Scholar
Schacht, M. (2016) Extremal results for random discrete structures. Ann. of Math. 184 333–365.CrossRefGoogle Scholar
Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 199–245.CrossRefGoogle Scholar
Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz Lapook 48 436–452.Google Scholar
van den Berg, J. and Jonasson, J. (2012) A BK inequality for randomly drawn subsets of fixed size. Probab. Theory Related Fields 154 835–844.CrossRefGoogle Scholar