Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T16:39:38.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On the mixing time of coordinate Hit-and-Run

Part of: Theory of computing

Published online by Cambridge University Press:  25 August 2021

Hariharan Narayanan  and
Piyush Srivastava
Hariharan Narayanan
Affiliation:
Tata Institute of Fundamental Research, Mumbai, Maharashtra, India
Piyush Srivastava*
Affiliation:
Tata Institute of Fundamental Research, Mumbai, Maharashtra, India
*
*Corresponding author. Email: piyush.srivastava@tifr.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a polynomial upper bound on the mixing time 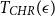$T_{CHR}(\epsilon)$ of the coordinate Hit-and-Run (CHR) random walk on an 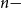$n-$ dimensional convex body, where 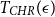$T_{CHR}(\epsilon)$ is the number of steps needed to reach within $\epsilon$ of the uniform distribution with respect to the total variation distance, starting from a warm start (i.e., a distribution which has a density with respect to the uniform distribution on the convex body that is bounded above by a constant). Our upper bound is polynomial in n, R and 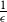$\frac{1}{\epsilon}$ , where we assume that the convex body contains the unit 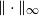$\Vert\cdot\Vert_\infty$ -unit ball 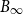$B_\infty$ and is contained in its R-dilation 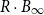$R\cdot B_\infty$ . Whether CHR has a polynomial mixing time has been an open question.

Keywords

Markov chainsConvex bodiesSampling

MSC classification

Primary: 68Q87: Probability in computer science (algorithm analysis, random structures, phase transitions, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 2 , March 2022 , pp. 320 - 332
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boucheron, S., Lugosi, G. and Massart, P. (2013) Concentration Inequalities: A Non-Asymptotic Theory of Independence. Oxford University Press.CrossRefGoogle Scholar
Chen, Y., Dwivedi, R., Wainwright, M. J. and Yu, B. (2018) Fast MCMC sampling algorithms on polytopes. J. Mach. Learn. Res. 19 2146–2231.Google Scholar
Cousins, B. (2017) Efficient High-Dimensional Sampling and Integration. PhD thesis, Georgia Institute of Technology.Google Scholar
Dyer, M., Frieze, A. and Kannan, R. (1991) A random polynomial-time algorithm for approximating the volume of convex bodies. J. ACM 38 1–17.CrossRefGoogle Scholar
Fallahi, S., Skaug, H. J. and Alendal, G. (2020) A comparison of Monte Carlo sampling methods for metabolic network models. PLoS One 15 e0235393.CrossRefGoogle ScholarPubMed
Haraldsdóttir, H. S., Cousins, B., Thiele, I., Fleming, R. M. T. and Vempala, S. S. (2017) CHRR: Coordinate hit-and-run with rounding for uniform sampling of constraint-based models. Bioinformatics 33 1741–1743.CrossRefGoogle ScholarPubMed
Kannan, R., Lovász, L. and Simonovits, M. (1997) Random walks and an ${O}^*(n^5)$ volume algorithm for convex bodies. Random Struct. Algor. 11 1–50.3.0.CO;2-X>CrossRefGoogle Scholar
Kannan, R. and Narayanan, H. (2012) Random walks on polytopes and an affine interior point method for linear programming. Math. Oper. Res. 37 1–20.CrossRefGoogle Scholar
Laddha, A. and Vempala, S. S. (2021) Convergence of Gibbs Sampling: Coordinate Hit-and-Run Mixes Fast. In Proceedings of the 37th International Symposium on Computational Geometry, (SoCG 2021), pp. 51:1–51:12. Also available at arXiv:2009.11338.Google Scholar
Laddha, A., Lee, Y. T. and Vempala, S. S. (2020) Strong self-concordance and sampling. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing (STOC 2020), pp. 1212–1222.CrossRefGoogle Scholar
Lee, Y. T. and Vempala, S. S. (2017) Geodesic walks in polytopes. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2017), pp. 927–940.CrossRefGoogle Scholar
Lee, Y. T. and Vempala, S. S. (2018) Convergence rate of Riemannian Hamiltonian Monte Carlo and faster polytope volume computation. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2018), pp. 1115–1121.CrossRefGoogle Scholar
Lee, Y. T. and Vempala, S. S. (2018) The Kannan-Lovász-Simonovits Conjecture. arXiv:1807.03465.Google Scholar
Lovász, L. (1999) Hit-and-run mixes fast. Math. Prog. 86 443–461.Google Scholar
Lovász, L. and Simonovits, M. (1993) Random walks in a convex body and an improved volume algorithm. Random Struct. Algor. 4 359–412.CrossRefGoogle Scholar
Lovász, L. and Vempala, S. (2006) Simulated annealing in convex bodies and an O *(n 4) volume algorithm J. Comput. Sys. Sci. 72 392–417.Google Scholar
Lovász, L. and Vempala, S. (2006) Hit-and-run from a corner. SIAM J. Comput. 35 985–1005.CrossRefGoogle Scholar
Mangoubi, O. and Vishnoi, N. K. (2019) Faster polytope rounding, sampling, and volume computation via a sub-linear ball walk. In Proceedings of the 60th IEEE Annual Symposium on Foundations of Computer Science (FOCS 2019), pp. 1338–1357.10.1109/FOCS.2019.00082CrossRefGoogle Scholar
Motwani, R. and Raghavan, P. (1995) Randomized Algorithms. Cambridge University Press.10.1017/CBO9780511814075CrossRefGoogle Scholar
Narayanan, H. (2016) Randomized interior point methods for sampling and optimization, Ann. Appl. Probab. 26 597–641.CrossRefGoogle Scholar
Smith, R. L. (1984) Efficient Monte-Carlo procedures for generating points uniformly distributed over bounded regions. Oper. Res. 32 1296–1308.CrossRefGoogle Scholar