Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T09:02:46.982Z Has data issue: false hasContentIssue false
  • English
  • Français

A Pair of Forbidden Subgraphs and 2-Factors

Published online by Cambridge University Press:  02 February 2012

JUN FUJISAWA  and
AKIRA SAITO
JUN FUJISAWA
Affiliation:
Faculty of Business and Commerce, Keio University, Hiyoshi 4–1–1, Kohoku-Ku, Yokohama, Kanagawa 223–8521, Japan (e-mail: fujisawa@fbc.keio.ac.jp)
AKIRA SAITO
Affiliation:
Department of Computer Science, Nihon University, Sakurajosui 3–25–40, Setagaya-Ku, Tokyo 156–8550, Japan (e-mail: asaito@chs.nihon-u.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider pairs of forbidden subgraphs that imply the existence of a 2-factor in a graph. For d ≥ 2, let 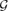d be the set of connected graphs of minimum degree at least d. Let F1 and F2 be connected graphs and let 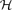be a set of connected graphs. Then {F1, F2} is said to be a forbidden pair for 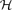if every {F1, F2}-free graph in 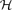of sufficiently large order has a 2-factor. Faudree, Faudree and Ryjáček have characterized all the forbidden pairs for the set of 2-connected graphs. We first characterize the forbidden pairs for 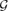2, which is a larger set than the set of 2-connected graphs, and observe a sharp difference between the characterized pairs and those obtained by Faudree, Faudree and Ryjáček. We then consider the forbidden pairs for connected graphs of large minimum degree. We prove that if {F1, F2} is a forbidden pair for 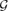d, then either F1 or F2 is a star of order at most d + 2. Ota and Tokuda have proved that every 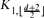-free graph of minimum degree at least d has a 2-factor. These results imply that for k ≥ d + 2, no connected graphs F except for stars of order at most d + 2 make {K1,k, F} a forbidden pair for 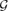d, while for 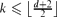every connected graph F makes {K1,k, F} a forbidden pair for 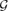d. We consider the remaining range of 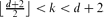, and prove that only a finite number of connected graphs F make {K1,k, F} a forbidden pair for 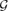d.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 149 - 158
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aldred, R. E. L., Fujisawa, J. and Saito, A. (2009) Two forbidden subgraphs and the existence of a 2-factor in graphs. Australasian J. Combin. 44 235–246.Google Scholar
[2]Aldred, R. E. L., Fujisawa, J. and Saito, A. (2010) Forbidden subgraphs and the existence of a 2-factor. J. Graph Theory 63 250–266.Google Scholar
[3]Chartrand, G. and Lesniak, L. (2005) Graphs and Digraphs, fourth edition, Chapman & Hall/CRC.Google Scholar
[4]Duffus, D., Jacobson, M. S. and Gould, R. J. (1981) Forbidden subgraphs and the Hamiltonian theme. In The Theory and Applications of Graphs, Wiley, pp. 297–316.Google Scholar
[5]Faudree, J. R., Faudree, F. J. and Ryjáček, Z. (2008) Forbidden subgraphs that imply 2-factors. Discrete Math. 308 1571–1582.Google Scholar
[6]Faudree, R. J. and Gould, R. J. (1997) Characterizing forbidden pairs for Hamiltonian properties. Discrete Math. 173 45–60.Google Scholar
[7]Fujita, S., Kawarabayashi, K., Lucchesi, C. L., Ota, K., Plummer, M. and Saito, A. (2006) A pair of forbidden subgraphs and perfect matchings. J. Combin. Theory Ser. B 96 315–324.Google Scholar
[8]Gould, R. J. and Jacobson, M. S. (1982) Forbidden subgraphs and Hamiltonian properties of graphs. Discrete Math. 42 189–196.CrossRefGoogle Scholar
[9]Ota, K. and Tokuda, T. (1996) A degree condition for the existence of regular factors in K1,n-free graphs. J. Graph Theory 22 59–64.3.0.CO;2-K>CrossRefGoogle Scholar
[10]Tutte, W. T. (1952) The factors of graphs. Canadian J. Math. 4 314–328.Google Scholar