Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-05T13:44:34.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Unavoidable patterns in locally balanced colourings

Part of: Graph theory

Published online by Cambridge University Press:  01 June 2023

Nina Kamčev Open the ORCID record for Nina Kamčev [Opens in a new window]  and
Alp Müyesser
Nina Kamčev*
Affiliation:
Department of Mathematics, Faculty of Science, University of Zagreb, Zagreb, Croatia
Alp Müyesser
Affiliation:
University College London, London, UK
*
Corresponding author: Nina Kamčev; Email: nina.kamcev@math.hr
Get access Rights & Permissions [Opens in a new window]

Abstract

Which patterns must a two-colouring of 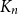$K_n$ contain if each vertex has at least 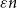$\varepsilon n$ red and 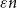$\varepsilon n$ blue neighbours? We show that when 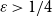$\varepsilon \gt 1/4$, 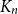$K_n$ must contain a complete subgraph on 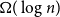$\Omega (\log n)$ vertices where one of the colours forms a balanced complete bipartite graph.

When 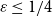$\varepsilon \leq 1/4$, this statement is no longer true, as evidenced by the following colouring 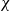$\chi$ of 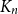$K_n$. Divide the vertex set into 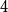$4$ parts nearly equal in size as 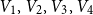$V_1,V_2,V_3, V_4$, and let the blue colour class consist of the edges between 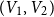$(V_1,V_2)$, 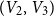$(V_2,V_3)$, 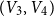$(V_3,V_4)$, and the edges contained inside 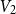$V_2$ and inside 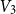$V_3$. Surprisingly, we find that this obstruction is unique in the following sense. Any two-colouring of 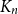$K_n$ in which each vertex has at least 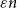$\varepsilon n$ red and 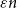$\varepsilon n$ blue neighbours (with 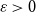$\varepsilon \gt 0$) contains a vertex set 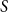$S$ of order 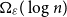$\Omega _{\varepsilon }(\log n)$ on which one colour class forms a balanced complete bipartite graph, or which has the same colouring as 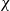$\chi$.

Keywords

Ramsey theoryunavoidable patterns

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C55: Generalized Ramsey theory 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 5 , September 2023 , pp. 796 - 808
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by the European Union’s Horizon 2020 research and innovation programme [MSCA GA No 101038085].

References

Bowen, M., Lamaison, A. and Müyesser, A. (2020) Finding unavoidable colorful patterns in multicolored graphs. Electron. J. Comb. 27(4) P4.4.Google Scholar
Caro, Y., Hansberg, A. and Montejano, A. (2021) Unavoidable chromatic patterns in 2-colorings of the complete graph. J. Graph Theory 97(1) 123–147.10.1002/jgt.22645CrossRefGoogle Scholar
Conlon, D. and Fox, J. (2013) Graph removal lemmas. In Surveys in Combinatorics 2013, Vol. 409 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 1–49.Google Scholar
Cutler, J. and Montágh, B. (2008) Unavoidable subgraphs of colored graphs. Discrete Math. 308(19) 4396–4413.10.1016/j.disc.2007.08.102CrossRefGoogle Scholar
Diestel, R. (2012) Graph Theory: Springer Graduate Text, Vol. 173, Reinhard Diestel.Google Scholar
Erdős, P. and Szekeres, G. (1935) A combinatorial problem in geometry. Compositio Math. 2 463–470.Google Scholar
Fox, J., Luo, S. and Wigderson, Y. (2021) Extremal and Ramsey results on graph blowups. J. Comb. 12(1) 1–15.Google Scholar
Fox, J. and Sudakov, B. (2008) Induced Ramsey-type theorems. Adv. Math. 219(6) 1771–1800.10.1016/j.aim.2008.07.009CrossRefGoogle Scholar
Fox, J. and Sudakov, B. (2008) Unavoidable patterns. J. Combin. Theory Ser. A 115(8) 1561–1569.10.1016/j.jcta.2008.04.003CrossRefGoogle Scholar
Fox, J. and Sudakov, B. (2011) Dependent random choice. Random Struct. Algorithms 38(1-2) 68–99.10.1002/rsa.20344CrossRefGoogle Scholar
Girão, A. and Hancock, R. (2022) Two Ramsey problems in blowups of graphs. arXiv preprint arXiv: 2205.12826 .Google Scholar
Girão, A. and Correia, D. M. (2022) A note on unavoidable patterns in locally dense colourings. arXiv preprint arXiv: 2211.01862 .Google Scholar
Girão, A. and Narayanan, B. (2022) Turán theorems for unavoidable patterns. Math. Proc. Cambridge Philos. Soc. 172(2) 423–442.10.1017/S030500412100027XCrossRefGoogle Scholar
Kővari, T., Sós, V. and Turán, P. (1954) On a problem of K. Zarankiewicz. Colloq. Math. 3(1) 50–57.10.4064/cm-3-1-50-57CrossRefGoogle Scholar
Müyesser, A. and Tait, M. (2022) Turán-and Ramsey-type results for unavoidable subgraphs. J. Graph Theory 101(4) 597–622.10.1002/jgt.22842CrossRefGoogle Scholar
Nagy, Z. L. (2019) Supersaturation of $C_4$ : from Zarankiewicz towards Erdős-Simonovits-Sidorenko. Eur. J. Comb. 75 19–31.10.1016/j.ejc.2018.07.015CrossRefGoogle Scholar
Nikiforov, V. (2008) Graphs with many $r$ -cliques have large complete $r$ -partite subgraphs. Bull. Lond. Math. Soc. 40(1) 23–25.10.1112/blms/bdm093CrossRefGoogle Scholar