Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T16:08:27.670Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform s-Cross-Intersecting Families

Published online by Cambridge University Press:  28 March 2017

PETER FRANKL  and
ANDREY KUPAVSKII
PETER FRANKL
Affiliation:
Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, P.O. Box 127, H-1364 Budapest, Hungary
ANDREY KUPAVSKII
Affiliation:
Moscow Institute of Physics and Technology, 9 Institutskiy per., 141701, Dolgoprudny, Russia École Polytechnique Fédérale de Lausanne, Station 8, 1015 Lausanne, Switzerland (e-mail: kupavskii@yandex.ru)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a question related to the classical Erdős–Ko–Rado theorem, which states that any family of k-element subsets of the set [n] = {1,. . .,n} in which any two sets intersect has cardinality at most 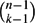$\binom{n-1}{k-1}$.

We say that two non-empty families 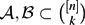${\mathcal A}, {\mathcal B}\subset \binom{[n]}{k}$ are s-cross-intersecting if, for any A ∈ 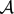${\mathcal A}$, B ∈ 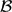${\mathcal B}$, we have |A ∩ B| ≥ s. In this paper we determine the maximum of |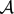${\mathcal A}$|+|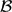${\mathcal B}$| for all n. This generalizes a result of Hilton and Milner, who determined the maximum of |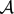${\mathcal A}$|+|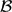${\mathcal B}$| for non-empty 1-cross-intersecting families.

Keywords

05D05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 4 , July 2017 , pp. 517 - 524
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. 12 313–320.Google Scholar
[2] Frankl, P. and Kupavskii, A. A size-sensitive inequality for cross-intersecting families, to appear in European Journal of Combinatorics, arXiv:1603.00936Google Scholar
[3] Frankl, P. and Tokushige, N. (1992) Some best possible inequalities concerning cross-intersecting families. J. Combin. Theory Ser. A 61 87–97.CrossRefGoogle Scholar
[4] Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Quart. J. Math. Oxford 18 369–384.Google Scholar
[5] Lau, L. C., Ravi, R. and Singh, M. (2011) Iterative Methods in Combinatorial Optimization, Cambridge University Press.Google Scholar