Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-11T03:43:21.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic Progressions in Sumsets and Lp-Almost-Periodicity

Published online by Cambridge University Press:  19 March 2013

ERNIE CROOT ,
IZABELLA ŁABA  and
OLOF SISASK
ERNIE CROOT
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA (e-mail: ecroot@math.gatech.edu)
IZABELLA ŁABA
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada (e-mail: ilaba@math.ubc.ca)
OLOF SISASK
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK (e-mail: O.Sisask@qmul.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove results about the Lp-almost-periodicity of convolutions. One of these follows from a simple but rather general lemma about approximating a sum of functions in Lp, and gives a very short proof of a theorem of Green that if A and B are subsets of {1,. . .,N} of sizes αN and βN then A+B contains an arithmetic progression of length at least

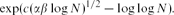\begin{equation} \exp ( c (\alpha \beta \log N)^{1/2} - \log\log N). \end{equation}
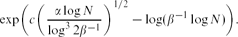Another almost-periodicity result improves this bound for densities decreasing with N: we show that under the above hypotheses the sumset A+B contains an arithmetic progression of length at least
\begin{equation} \exp\biggl( c \biggl(\frac{\alpha \log N}{\log^3 2\beta^{-1}} \biggr)^{1/2} - \log( \beta^{-1} \log N) \biggr). \end{equation}

Keywords

Primary 11B30Secondary 11B25
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 3 , May 2013 , pp. 351 - 365
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bourgain, J. (1990) On arithmetic progressions in sums of sets of integers. In A Tribute to Paul Erdős, Cambridge University Press, pp. 105–109.Google Scholar
[2]Chang, M.-C. (2002) A polynomial bound in Freiman's theorem. Duke Math. J. 113 399–419.Google Scholar
[3]Croot, E. and Sisask, O. (2010) A probabilistic technique for finding almost-periods of convolutions. Geom. Funct. Anal. 20 1367–1396.Google Scholar
[4]Green, B. (2002) Arithmetic progressions in sumsets. Geom. Funct. Anal. 12 584–597.Google Scholar
[5]Green, B. (2002) Restriction and Kakeya Phenomena, lecture notes. http://www.dpmms.cam.ac.uk/~bjg23/rkp.htmlGoogle Scholar
[6]Green, B. (2005) Finite field models in additive combinatorics. In Surveys in Combinatorics 2005, Vol. 327 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 1–27.Google Scholar
[7]Gut, A. (2005) Probability: A Graduate Course, Springer.Google Scholar
[8]Khintchine, A. (1923) Über dyadische Brüche. Math. Z. 18 109–116.Google Scholar
[9]Petridis, G. (2013) New proofs of Plünnecke-type estimates for product sets in groups. Combinatorica, doi: 10.1007/s00493-012-2818-5.Google Scholar
[10]Pisier, G. (1981) Remarques sur un résultat non publié de B. Maurey. In Seminar on Functional Analysis, 1980–1981, exp. no. 5, École Polytechnique, Palaiseau. http://www.numdam.org/item?id=SAF_1980-1981____A5_0Google Scholar
[11]Ruzsa, I. Z. (2009) Sumsets and structure. In Combinatorial Number Theory and Additive Group Theory, Springer, pp. 87–210.Google Scholar
[12]Sanders, T. (2008) Additive structures in sumsets. Math. Proc. Cambridge Philos. Soc. 144 289–316.Google Scholar
[13]Sanders, T. (2011) Green's sumset problem at density one half. Acta Arith. 146 91–101.Google Scholar
[14]Sanders, T. (2012) On the Bogolyubov–Ruzsa lemma. Anal. PDE 5 627–655.Google Scholar
[15]Tao, T. and Vu, V. H. (2006) Additive Combinatorics, Cambridge University Press.Google Scholar