Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T08:03:25.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Properties of Some Minor-Closed Classes of Graphs

Published online by Cambridge University Press:  09 July 2014

MIREILLE BOUSQUET-MÉLOU  and
KERSTIN WELLER
MIREILLE BOUSQUET-MÉLOU
Affiliation:
MBM: CNRS, LaBRI, UMR 5800, Université de Bordeaux, 351 Cours de la Libération, 33405 Talence Cedex, France (e-mail: mireille.bousquet@labri.fr)
KERSTIN WELLER
Affiliation:
KW: Department of Statistics, University of Oxford, 1 South Parks Road, Oxford, OX1 3TG, UK (e-mail: weller@stats.ox.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 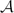${\cal A}$ be a minor-closed class of labelled graphs, and let 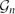${\cal G}_{n}$ be a random graph sampled uniformly from the set of n-vertex graphs of 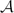${\cal A}$. When n is large, what is the probability that 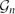${\cal G}_{n}$ is connected? How many components does it have? How large is its biggest component? Thanks to the work of McDiarmid and his collaborators, these questions are now solved when all excluded minors are 2-connected.

Using exact enumeration, we study a collection of classes 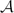${\cal A}$ excluding non-2-connected minors, and show that their asymptotic behaviour may be rather different from the 2-connected case. This behaviour largely depends on the nature of the dominant singularity of the generating function C(z) that counts connected graphs of 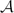${\cal A}$. We classify our examples accordingly, thus taking a first step towards a classification of minor-closed classes of graphs. Furthermore, we investigate a parameter that has not received any attention in this context yet: the size of the root component. It follows non-Gaussian limit laws (Beta and Gamma), and clearly merits a systematic investigation.

Keywords

Primary 05A1505C30Secondary 05C8360C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 5: Honouring the Memory of Philippe Flajolet - Part 1 , September 2014 , pp. 749 - 795
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Addario-Berry, L., McDiarmid, C. and Reed, B. (2012) Connectivity for bridge-addable monotone graph classes. Combin. Probab. Comput. 21 803–815.Google Scholar
[2]Arratia, R., Barbour, A. D. and Tavaré, S. (2003) Logarithmic Combinatorial Structures: A Probabilistic Approach, EMS Monographs in Mathematics, European Mathematical Society.CrossRefGoogle Scholar
[3]Banderier, C., Flajolet, P., Schaeffer, G. and Soria, M. (2001) Random maps, coalescing saddles, singularity analysis, and Airy phenomena. Random Struct. Alg. 19 194–246.Google Scholar
[4]Bell, J. P., Bender, E. A., Cameron, P. J. and Richmond, L. B. (2000) Asymptotics for the probability of connectedness and the distribution of number of components. Electron. J. Combin. 7 R33.Google Scholar
[5]Bender, E. A. (1974) Asymptotic methods in enumeration. SIAM Review 16 485–515.Google Scholar
[6]Bernardi, O., Noy, M. and Welsh, D. (2010) Growth constants of minor-closed classes of graphs. J. Combin. Theory Ser. B 100 468–484.Google Scholar
[7]Bernasconi, N., Panagiotou, K. and Steger, A. (2008) On the degree sequences of random outerplanar and series-parallel graphs. In Approximation, Randomization and Combinatorial Optimization, Vol. 5171 of Lecture Notes in Computer Science, Springer, pp. 303–316.Google Scholar
[8]Bernasconi, N., Panagiotou, K. and Steger, A. (2009) The degree sequence of random graphs from subcritical classes. Combin. Probab. Comput. 18 647–681.Google Scholar
[9]Billingsley, P. (1999) Convergence of Probability Measures, second edition, Wiley Series in Probability and Statistics, Wiley.Google Scholar
[10]Bousquet-Mélou, M. and Weller, K. Size of the root component in exponential structures. In preparation.Google Scholar
[11]Canfield, E. R. (1977) Central and local limit theorems for the coefficients of polynomials of binomial type. J. Combin. Theory Ser. A 23 275–290.Google Scholar
[12]Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J. and Knuth, D. E. (1996) On the Lambert W function. Adv. Comput. Math. 5 329–359.Google Scholar
[13]Darrasse, A., Panagiotou, K., Roussel, O. and Soria, M. (2012) Biased Boltzmann samplers and generation of extended linear languages with shuffle. In Proc. 23rd International Meeting on Probabilistic, Combinatorial, and Asymptotic Methods in the Analysis of Algorithms: AofA'12, pp. 125–140.CrossRefGoogle Scholar
[14]Drmota, M., Fusy, É., Kang, M., Kraus, V. and Rué, J. (2011) Asymptotic study of subcritical graph classes. SIAM J. Discrete Math. 25 1615–1651.Google Scholar
[15]Drmota, M., Giménez, O. and Noy, M. (2011) Degree distribution in random planar graphs. J. Combin. Theory Ser. A 118 2102–2130.Google Scholar
[16]Drmota, M., Gittenberger, B. and Klausner, T. (2005) Extended admissible functions and Gaussian limiting distributions. Math. Comp. 74 1953–1966.CrossRefGoogle Scholar
[17]Drmota, M. and Soria, M. (1995) Marking in combinatorial constructions: Generating functions and limiting distributions. Theoret. Comput. Sci. 144 67–99.Google Scholar
[18]Duchon, P., Flajolet, P., Louchard, G. and Schaeffer, G. (2004) Boltzmann samplers for the random generation of combinatorial structures. Combin. Probab. Comput. 13 577–625.Google Scholar
[19]Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.Google Scholar
[20]Giménez, O., Noy, M. and Rué, J. (2013) Graph classes with given 3-connected components: Asymptotic enumeration and random graphs. Random Struct. Alg. 42 438–479.Google Scholar
[21]Gourdon, X. (1998) Largest component in random combinatorial structures. Discrete Math. 180 185–209.Google Scholar
[22]Hayman, W. K. (1956) A generalisation of Stirling's formula. J. Reine Angew. Math. 196 67–95.Google Scholar
[23]Kang, M. and Panagiotou, K. (2013) On the connectivity of random graphs from addable classes. J. Combin. Theory Ser. B 103 306–312.Google Scholar
[24]Kolchin, V. F. (1999) Random Graphs, Vol. 53 of Encyclopedia of Mathematics and its Applications, Cambridge University Press.Google Scholar
[25]Macintyre, A. J. and Wilson, R. (1954) Operational methods and the coefficients of certain power series. Math. Ann. 127 243–250.Google Scholar
[26]McDiarmid, C. (2009) Random graphs from a minor-closed class. Combin. Probab. Comput. 18 583–599.Google Scholar
[27]McDiarmid, C. (2011) On graphs with few disjoint t-star minors. Europ. J. Combin. 32 1394–1406.Google Scholar
[28]McDiarmid, C., Steger, A. and Welsh, D. J. A. (2005) Random planar graphs. J. Combin. Theory Ser. B 93 187–205.Google Scholar
[29]McDiarmid, C., Steger, A. and Welsh, D. J. A. (2006) Random graphs from planar and other addable classes. In Topics in Discrete Mathematics, Vol. 26 of Algorithms Combin., Springer, pp. 231–246.Google Scholar
[30]Norine, S., Seymour, P., Thomas, R. and Wollan, P. (2006) Proper minor-closed families are small. J. Combin. Theory Ser. B 96 754–757.CrossRefGoogle Scholar
[31]Rényi, A. (1959) On connected graphs I. Magyar Tud. Akad. Mat. Kutató Int. Közl. 4 385–388.Google Scholar
[32]Robertson, N. and Seymour, P. D. (1983–2004) Graph minors I–XX. J. Combin. Theory Ser. B.Google Scholar
[33]Stanley, R. P. (1999) Enumerative Combinatorics 2, Vol. 62 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
[34]Wright, E. M. (1977) The number of connected sparsely edged graphs. J. Graph Theory 1 317–330.Google Scholar