Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fan, Genghua
Xu, Baogang
Yu, Xingxing
and
Zhou, Chuixiang
2012.
Upper bounds on minimum balanced bipartitions.
Discrete Mathematics,
Vol. 312,
Issue. 6,
p.
1077.
Tian, Fang
and
Liu, Zi-Long
2012.
Simple probabilistic analysis to generalize bottleneck graph multi-partitioning.
Applied Mathematics Letters,
Vol. 25,
Issue. 12,
p.
2040.
Xu, Baogang
and
Yu, Xingxing
2014.
On judicious bisections of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 106,
Issue. ,
p.
30.
LI, HAIYAN
and
XU, BAOGANG
2014.
MAXIMUM BALANCED 3-PARTITIONS OF GRAPHS.
Discrete Mathematics, Algorithms and Applications,
Vol. 06,
Issue. 02,
p.
1450020.
Fan, Genghua
Hou, Jianfeng
and
Zeng, Qinghou
2014.
A bound for judiciousk-partitions of graphs.
Discrete Applied Mathematics,
Vol. 179,
Issue. ,
p.
86.
Liu, Muhuo
and
Xu, Baogang
2016.
On judicious partitions of graphs.
Journal of Combinatorial Optimization,
Vol. 31,
Issue. 4,
p.
1383.
Ma, Jie
and
Yu, Xingxing
2016.
On judicious bipartitions of graphs.
Combinatorica,
Vol. 36,
Issue. 5,
p.
537.
Xu, Xin
Yan, GuiYing
and
Zhang, Yao
2016.
Judicious partitions of weighted hypergraphs.
Science China Mathematics,
Vol. 59,
Issue. 3,
p.
609.
Fan, Genghua
and
Hou, Jianfeng
2017.
Bounds for pairs in judicious partitioning of graphs.
Random Structures & Algorithms,
Vol. 50,
Issue. 1,
p.
59.
Zeng, Qing Hou
Hou, Jian Feng
Deng, Jin
and
Lei, Xia
2017.
Biased partitions and judicious k-partitions of graphs.
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 5,
p.
668.
Hou, Jianfeng
and
Zeng, Qinghou
2017.
On a Problem of Judiciousk-Partitions of Graphs.
Journal of Graph Theory,
Vol. 85,
Issue. 3,
p.
619.
Hou, Jianfeng
Wu, Shufei
Zeng, Qinghou
and
Zhu, Wenxing
2018.
The Bollobás--Scott Conjecture for 4-Uniform Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 1,
p.
505.
FAN, GENGHUA
HOU, JIANFENG
and
YU, XINGXING
2018.
Bisections of Graphs Without Short Cycles.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 1,
p.
44.
Hou, Jianfeng
and
Wu, Shufei
2018.
Bipartitions of oriented graphs.
Journal of Combinatorial Theory, Series B,
Vol. 132,
Issue. ,
p.
107.
Cao, Fayun
Luo, Yujiao
and
Ren, Han
2018.
Bounds for Judicious Balanced Bipartitions of Graphs.
Graphs and Combinatorics,
Vol. 34,
Issue. 6,
p.
1175.
Wu, Shufei
and
Hou, Jianfeng
2018.
Partitioning dense uniform hypergraphs.
Journal of Combinatorial Optimization,
Vol. 35,
Issue. 1,
p.
48.
Ji, Yuliang
Ma, Jie
Yan, Juan
and
Yu, Xingxing
2019.
On problems about judicious bipartitions of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 139,
Issue. ,
p.
230.
Ma, Huawen
2020.
Maximum Cuts in $$\mathscr {H}$$-Free Graphs.
Graphs and Combinatorics,
Vol. 36,
Issue. 5,
p.
1503.
Hou, Jianfeng
Li, Zhe
and
Wu, Shufei
2020.
On bipartitions of directed graphs with small semidegree.
European Journal of Combinatorics,
Vol. 84,
Issue. ,
p.
103039.
Chen, Tao
2021.
Bisection of Hamilton Plane Graphs under Girth Constraints.
Journal of Physics: Conference Series,
Vol. 1769,
Issue. 1,
p.
012043.

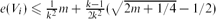 for
for 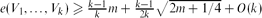 , where
, where 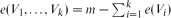 . This answers a problem of Bollobás and Scott [2] in the affirmative. Moreover,
. This answers a problem of Bollobás and Scott [2] in the affirmative. Moreover, 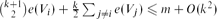 for
for 