Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:47:15.713Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressions and Probably Intersecting Families

Published online by Cambridge University Press:  02 February 2012

PAUL A. RUSSELL
PAUL A. RUSSELL*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: P.A.Russell@dpmms.cam.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

A family 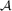of sets is said to be intersecting if A ∩ B ≠ ∅ for all A, B ∈ 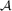. It is a well-known and simple fact that an intersecting family of subsets of [n] = {1, 2, . . ., n} can contain at most 2n−1 sets. Katona, Katona and Katona ask the following question. Suppose instead 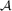⊂ 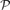[n] satisfies |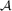| = 2n−1 + i for some fixed i > 0. Create a new family 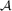p by choosing each member of 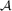independently with some fixed probability p. How do we choose 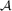to maximize the probability that 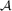p is intersecting? They conjecture that there is a nested sequence of optimal families for i = 1, 2,. . ., 2n−1. In this paper, we show that the families [n](≥r) = {A ⊂ [n]: |A| ≥ r} are optimal for the appropriate values of i, thereby proving the conjecture for this sequence of values. Moreover, we show that for intermediate values of i there exist optimal families lying between those we have found. It turns out that the optimal families we find simultaneously maximize the number of intersecting subfamilies of each possible order.

Standard compression techniques appear inadequate to solve the problem as they do not preserve intersection properties of subfamilies. Instead, our main tool is a novel compression method, together with a way of ‘compressing subfamilies’, which may be of independent interest.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 301 - 313
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ahlswede, R. and Khachatrian, L. H. (2005) Katona's intersection theorem: four proofs. Combinatorica 25 105–110.CrossRefGoogle Scholar
[2]Bollobás, B. and Leader, I. (1991) Compressions and isoperimetric inequalities. J. Combin. Theory Ser. A 56 47–62.CrossRefGoogle Scholar
[3]Daykin, D. E. (1974) A simple proof of the Kruskal–Katona theorem. J. Combin. Theory, Ser. A 17 252–253.CrossRefGoogle Scholar
[4]Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. L. Math. Oxford (2) 12 313–320.CrossRefGoogle Scholar
[5]Frankl, P. and Füredi, Z. (1983) A short proof of a theorem of Harper about Hamming-spheres. Discrete Math. 34 311–313.CrossRefGoogle Scholar
[6]Katona, G. O. H. (1964) Intersection theorems for systems of finite sets. Acta Math. Acad. Sci. Hungar. 15 329–337.CrossRefGoogle Scholar
[7]Katona, G. O. H. (1968) A theorem of finite sets. In Theory of Graphs: Proc. Colloq. Tihany 1966, Academic Press, pp. 187–207.Google Scholar
[8]Katona, G. O. H., Katona, G. Y. and Katona, Z. (2005) Probably intersecting families. Talk by G. O. H. Katona at the 12th International Conference on Random Structures and Algorithms, Poznań 2005.Google Scholar
[9]Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques, University of California Press, pp. 251–278.CrossRefGoogle Scholar
[10]Leader, I. B. (1999) personal communication.Google Scholar