Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-30T19:08:46.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Connectivity for Bridge-Addable Monotone Graph Classes

Published online by Cambridge University Press:  30 July 2012

L. ADDARIO-BERRY ,
C. MCDIARMID  and
B. REED
L. ADDARIO-BERRY
Affiliation:
Department of Statistics, 1 South Parks Road, Oxford, OX1 3TG, UK (e-mail: louigi@gmail.com, cmcd@stats.ox.ac.uk)
C. MCDIARMID
Affiliation:
Department of Statistics, 1 South Parks Road, Oxford, OX1 3TG, UK (e-mail: louigi@gmail.com, cmcd@stats.ox.ac.uk)
B. REED
Affiliation:
School of Computer Science, McGill University, 3480 University Street, Montreal, Quebec, H3A 2A7, Canada (e-mail: breed@cs.mcgill.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

A class 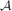of labelled graphs is bridge-addable if, for all graphs G in 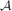and all vertices u and v in distinct connected components of G, the graph obtained by adding an edge between u and v is also in 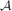; the class 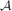is monotone if, for all G ∈ 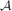and all subgraphs H of G, we have H ∈ 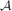. We show that for any bridge-addable, monotone class 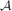whose elements have vertex set {1,. . .,n}, the probability that a graph chosen uniformly at random from 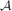is connected is at least (1−on(1))e−½, where on(1) → 0 as n → ∞. This establishes the special case of the conjecture of McDiarmid, Steger and Welsh when the condition of monotonicity is added. This result has also been obtained independently by Kang and Panagiotou.

Keywords

Primary 05C80Secondary 60C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 6 , November 2012 , pp. 803 - 815
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Balister, P., Bollobás, B. and Gerke, S. (2008) Connectivity of addable graph classes. J. Combin. Theory Ser. B 98 577–584.Google Scholar
[2]Balister, P., Bollobás, B. and Gerke, S. (2010) Connectivity of random addable graphs. In Proc. ICDM 2008, Vol. 13, pp. 127–134.Google Scholar
[3]Bender, E. and Gao, Z. (2011) Asymptotic enumeration of labelled graphs by genus. Electron. J. Combin. 18 P13.Google Scholar
[4]Bernardi, O., Noy, M. and D. Welsh, D. (2010) Growth constants of minor-closed classes of graphs. J. Combin. Theory Ser. B 100 468–484.Google Scholar
[5]Bodirsky, M., Giménez, O., Kang, M. and Noy, M. (2005) On the number of series parallel and outerplanar graphs. In Proc. European Conference on Combinatorics, Graph Theory, and Applications: EuroComb '05, DMTCS Proceedings Series, pp. 383–388.Google Scholar
[6]Bodirsky, M., Giménez, O., Kang, M. and Noy, M. (2007) Enumeration and limit laws for series-parallel graphs. Europ. J. Combin. 28 2091–2105.Google Scholar
[7]Bollobás, B. (2001) Random Graphs, second edition, Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
[8]Cayley, A. (1889) A theorem on trees. Quart. J. Math. 23 376–378.Google Scholar
[9]Chapuy, G., Fusy, E., Giménez, O., Mohar, B. and Noy, M. (2011) Asymptotic enumeration and limit laws for graphs of fixed genus. J. Combin. Theory Ser. A 118 748–777.Google Scholar
[10]Fountoulakis, N. and Panagiotou, K. (2011) 3-connected cores in random planar graphs. Combin. Probab. Comput. 20 381–412.Google Scholar
[11]Gerke, S., Giménez, O., Noy, M. and Weißl, A. (2008) The number of graphs not containing K3,3 as a minor. Electron. J. Combin. 15 R114.Google Scholar
[12]Giménez, O., Noy, M. and Rué, J.J. (2007) Graph classes with given 3-connected components: asymptotic counting and critical phenomena. Electron. Notes Discrete Math. 29 521–529.Google Scholar
[13]Giménez, O. and Noy, M. (2009) Asymptotic enumeration and limit laws of planar graphs. J. Amer. Math. Soc. 22 309–329.Google Scholar
[14]Giménez, O. and Noy, M. (2009) Counting planar graphs and related families of graphs. In Surveys in Combinatorics 2009, Cambridge University Press, pp. 169–329.Google Scholar
[15]Kang, M. and Panagiotou, K. (2012) On the connectivity of random graphs from addable classes. Submitted.Google Scholar
[16]McDiarmid, C., Steger, A. and Welsh, D. (2005) Random planar graphs. J. Combin. Theory Ser. B 93 187–206.Google Scholar
[17]McDiarmid, C., Steger, A. and Welsh, D. (2006) Random graphs from planar and other addable classes. In Topics in Discrete Mathematics: Dedicated to Jarik Nešetřil on the Occasion of his 60th Birthday (Klazar, M., Kratochvíl, J., Loebl, M., Matoušek, J., Thomas, R., and Valtr, P., eds), Vol. 26 of Algorithms and Combinatorics, Springer, pp. 231–246.Google Scholar
[18]Moon, J.W. (1970) Counting Labelled Trees, Vol. 1 of Canadian Mathematical Monographs, Canadian Mathematical Congress.Google Scholar
[19]Rényi, A. (1959) Some remarks on the theory of trees. Publ. Math. Inst. Hungarian Acad. Sci. 4 73–85.Google Scholar
[20]West, D.B. (2001) Introduction to Graph Theory, second edition, Prentice-Hall.Google Scholar