Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T23:14:53.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Cycle partitions of regular graphs

Part of: Graph theory

Published online by Cambridge University Press:  18 December 2020

Vytautas Gruslys  and
Shoham Letzter
Vytautas Gruslys
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK Email: v.gruslys@gmail.com
Shoham Letzter*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK Email: v.gruslys@gmail.com
*
*Corresponding author. Email: s.letzter@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnant and Martin conjectured that the vertex set of any d-regular graph G on n vertices can be partitioned into 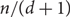$n / (d+1)$ paths (there exists a simple construction showing that this bound would be best possible). We prove this conjecture when 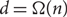$d = \Omega(n)$ , improving a result of Han, who showed that in this range almost all vertices of G can be covered by 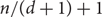$n / (d+1) + 1$ vertex-disjoint paths. In fact our proof gives a partition of V(G) into cycles. We also show that, if 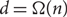$d = \Omega(n)$ and G is bipartite, then V(G) can be partitioned into n/(2d) paths (this bound is tight for bipartite graphs).

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Secondary: 05C38: Paths and cycles
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 4 , July 2021 , pp. 526 - 549
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research was supported by Dr Max Rössler, by theWalter Haefner Foundation and by the ETH Zurich Foundation.

References

Balogh, J., Mousset, F. and Skokan, J. (2017) An extension of Dirac’s theorem. Electron. J. Combin. 24 #P3.56.Google Scholar
Bollobás, B. (1978) Extremal Graph Theory. Academic Press.Google Scholar
Bollobás, B. and Hobbs, A. (1978) Hamiltonian cycles in regular graphs. Adv. Graph Theory 3 43–48.CrossRefGoogle Scholar
Broersma, H. J., van den Heuvel, J., Jackson, B. and Veldman, H. J. (1996). Hamiltonicity of regular 2-connected graphs. J. Graph Theory 22 105–124.3.0.CO;2-R>CrossRefGoogle Scholar
DeBiasio, L. and Nelsen, L. (2017) Monochromatic cycle partitions of graphs with large minimum degree. J. Combin. Theory Ser. B 122 634–667.CrossRefGoogle Scholar
Enomoto, H., Kaneko, A. and Tuza, Z. (1988) Graphs of order n and minimum degree n/4. In Combinatorics (Proc. Coll. Math. Soc. János Bolyai, Eger, 1987), pp. 213–220. North-Holland.Google Scholar
Erdös, P. and Hobbs, A. M. (1978) A class of Hamiltonian regular graphs. J. Graph Theory 2 129–135.CrossRefGoogle Scholar
Fan, G. (1985) Longest cycles in regular graphs. J. Combin. Theory Ser. B 39 325–345.CrossRefGoogle Scholar
Häggkvist, R. (1978) Unsolved problems. In Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely 1976), Vol. 18 of Colloquia Mathematica Societatis János Bolyai. North-Holland.Google Scholar
Han, J. (2018) On vertex-disjoint paths in regular graphs. Electron. J. Combin. 25 #P2.12.CrossRefGoogle Scholar
Hilbig, F. (1986) Kantenstrukturen in nichthamiltonischen Graphen. PhD thesis, Technical University Berlin.Google Scholar
Jackson, B. (1980) Hamilton cycles in regular 2-connected graphs. J. Combin. Theory Ser. B 29 27–46.CrossRefGoogle Scholar
Jackson, B. and Li, H. (1994) Hamilton cycles in 2-connected regular bipartite graphs. J. Combin. Theory Ser. B 62 236–258.CrossRefGoogle Scholar
Jackson, B., Li, H. and Zhu, Y. (1992) Dominating cycles in regular 3-connected graphs. Discrete Math. 102 163–176.CrossRefGoogle Scholar
Jung, H. A. (1984) Longest circuits in 3-connected graphs. In Finite and Infinite Sets, Vol. 37 of Colloquia Mathematica Societatis János Bolyai, pp. 403–438. Elsevier.CrossRefGoogle Scholar
Kouider, M. (1994) Covering vertices by cycles. J. Graph Theory 18 757–776.CrossRefGoogle Scholar
Kouider, M. and Lonc, Z. (1996) Covering cycles and k-term degree sums. Combinatorica 16 407–412.CrossRefGoogle Scholar
Kühn, D., Lo, A., Osthus, D. and Staden, K. (2015) The robust component structure of dense regular graphs and applications. Proc. London Math. Soc. 110 19–56.Google Scholar
Kühn, D., Lo, A., Osthus, D. and Staden, K. (2016) Solution to a problem of Bollobás and Häggkvist on Hamilton cycles in regular graphs. J. Combin. Theory Ser. B 121 85–145.CrossRefGoogle Scholar
Kühn, D. Mycroft, R. and Osthus, D. (2011) A proof of Sumner’s universal tournament conjecture for large tournaments. Proc. London Math. Soc. 102 731–766.CrossRefGoogle Scholar
Kühn, D. Mycroft, R. and Osthus, D. (2011) An approximate version of Sumner’s universal tournament conjecture. J. Combin. Theory Ser. B 101 415–447.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2013) Hamilton partitions of regular expanders: a proof of Kelly’s conjecture for large tournaments. Adv. Math. 237 62–146.CrossRefGoogle Scholar
Kühn, D., Osthus, D. and Treglown, A. (2010) Hamiltonian degree sequences in digraphs. J. Combin. Theory Ser. B 100 367–380.CrossRefGoogle Scholar
Li, H. (2013) Generalizations of Dirac’s theorem in Hamiltonian graph theory: a survey. Discrete Math. 313 2034–2053.CrossRefGoogle Scholar
Lo, A. and Patel, V. (2018) Hamilton cycles in sparse robustly expanding digraphs. Electron. J. Combin. 25 #3.44.CrossRefGoogle Scholar
Magnant, C. and Martin, D. (2009) A note on the path cover number of regular graphs. Australas. J. Combin. 43 211–217.Google Scholar
Nash-Williams, C. St J. A. (1971) Hamiltonian arcs and circuits. In Recent Trends in Graph Theory, Vol. 186 of Lecture Notes in Mathematics, pp. 197–210. Springer.CrossRefGoogle Scholar
Zhu, Y. and Li, H. (1992) Hamilton cycles in regular 3-connected graphs. Discrete Math. 110 229–249.CrossRefGoogle Scholar