Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Łuczak, Tomasz
1994.
Phase transition phenomena in random discrete structures.
Discrete Mathematics,
Vol. 136,
Issue. 1-3,
p.
225.
Hansen, Jennie
and
Jaworski, Jerzy
2000.
Large components of bipartite random mappings.
Random Structures and Algorithms,
Vol. 17,
Issue. 3-4,
p.
317.
Kang, Mihyun
Koh, Youngmee
Ree, Sangwook
and
Łuczak, Tomasz
2006.
The connectivity threshold for the min‐degree random graph process.
Random Structures & Algorithms,
Vol. 29,
Issue. 1,
p.
105.
Hansen, Jennie C.
and
Jaworski, Jerzy
2007.
A cutting process for random mappings.
Random Structures & Algorithms,
Vol. 30,
Issue. 1-2,
p.
287.
Coja-Oghlan, Amin
and
Kang, Mihyun
2009.
The evolution of the min–min random graph process.
Discrete Mathematics,
Vol. 309,
Issue. 13,
p.
4527.
Hansen, Jennie C.
and
Jaworski, Jerzy
2009.
A random mapping with preferential attachment.
Random Structures & Algorithms,
Vol. 34,
Issue. 1,
p.
87.

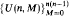 in which the minimum degree of
in which the minimum degree of 