Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T07:41:38.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Defective and clustered choosability of sparse graphs

Part of: Graph theory

Published online by Cambridge University Press:  12 April 2019

Kevin Hendrey  and
David R. Wood
Kevin Hendrey
Affiliation:
School of Mathematical Sciences, Monash University, Melbourne, Australia
David R. Wood*
Affiliation:
School of Mathematical Sciences, Monash University, Melbourne, Australia
*
*Corresponding author. Email: david.wood@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

An (improper) graph colouring has defect d if each monochromatic subgraph has maximum degree at most d, and has clustering c if each monochromatic component has at most c vertices. This paper studies defective and clustered list-colourings for graphs with given maximum average degree. We prove that every graph with maximum average degree less than (2d+2)/(d+2)k is k-choosable with defect d. This improves upon a similar result by Havet and Sereni (J. Graph Theory, 2006). For clustered choosability of graphs with maximum average degree m, no (1-ɛ)m bound on the number of colours was previously known. The above result with d=1 solves this problem. It implies that every graph with maximum average degree m is 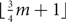$\lfloor{\frac{3}{4}m+1}\rfloor$-choosable with clustering 2. This extends a result of Kopreski and Yu (Discrete Math., 2017) to the setting of choosability. We then prove two results about clustered choosability that explore the trade-off between the number of colours and the clustering. In particular, we prove that every graph with maximum average degree m is 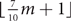$\lfloor{\frac{7}{10}m+1}\rfloor$-choosable with clustering 9, and is 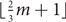$\lfloor{\frac{2}{3}m+1}\rfloor$-choosable with clustering O(m). As an example, the later result implies that every biplanar graph is 8-choosable with bounded clustering. This is the best known result for the clustered version of the earth–moon problem. The results extend to the setting where we only consider the maximum average degree of subgraphs with at least some number of vertices. Several applications are presented.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 5 , September 2019 , pp. 791 - 810
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albertson, M. O., Boutin, D. L., and Gethner, E.(2011) More results on r-inflated graphs: Arboricity, thickness, chromatic number and fractional chromatic number. Ars Math. Contemp. 4 5–24.CrossRefGoogle Scholar
Alon, N., Ding, G., Oporowski, B., and Vertigan, D. (2003) Partitioning into graphs with only small components. J. Combin. Theory Ser. B 87 231–243.CrossRefGoogle Scholar
Archdeacon, D. (1987) A note on defective colorings of graphs in surfaces. J. Graph Theory 11 517–519.CrossRefGoogle Scholar
Borodin, O. V. and Ivanova, A. O. (2009) Almost proper 2-colorings of vertices of sparse graphs. Diskretn. Anal. Issled. Oper. 16 16–20, 98.Google Scholar
Borodin, O. V., and Ivanova, A. O. (2011) List strong linear 2-arboricity of sparse graphs. J. Graph Theory 67 83–90.CrossRefGoogle Scholar
Borodin, O. V., Ivanova, A. O., Montassier, M., Ochem, P. and André Raspaud, A. (2010) Vertex decompositions of sparse graphs into an edgeless subgraph and a subgraph of maximum degree at most k. J. Graph Theory 65 83–93.CrossRefGoogle Scholar
Borodin, O. V., Ivanova, A. O., Montassier, M., and Raspaud, A. (2011) (k,j)-coloring of sparse graphs. Discrete Appl. Math. 159 1947–1953.CrossRefGoogle Scholar
Borodin, O. V., Ivanova, A. O., Montassier, M., and Raspaud, A. (2012) (k,1)-coloring of sparse graphs. Discrete Math. 312 1128–1135.CrossRefGoogle Scholar
Borodin, O. V. and Kostochka, A. V. (2011) Vertex decompositions of sparse graphs into an independent set and a subgraph of maximum degree at most 1. Sibirsk. Mat. Zh. 52 1004–1010.Google Scholar
Borodin, O. V. and Kostochka, A. V. (2014) Defective 2-colorings of sparse graphs. J. Combin. Theory Ser. B 104 72–80.CrossRefGoogle Scholar
Borodin, O. V., Kostochka, A. V., and Yancey, M. (2013) On 1-improper 2-coloring of sparse graphs. Discrete Math. 313 2638–2649.CrossRefGoogle Scholar
Boutin, D. L., Gethner, E., and Sulanke, T. (2008) Thickness-two graphs, part 1: New nine-critical graphs, permuted layer graphs, and Catlin’s graphs. J. Graph Theory 57 198–214.CrossRefGoogle Scholar
Choi, I. and Esperet, L. (2019) Improper coloring of graphs on surfaces. J. Graph Theory 91 16–34.CrossRefGoogle Scholar
Cowen, L. J., Cowen, R. H., and Woodall, D. R. (1986) Defective colorings of graphs in surfaces: Partitions into subgraphs of bounded valency. J. Graph Theory 10 187–195.CrossRefGoogle Scholar
Cowen, L., Goddard, W., and Jesurum, C. E. (1997 ) Defective coloring revisited. J. Graph Theory 24 205–219.3.0.CO;2-T>CrossRefGoogle Scholar
Cushing, W. and Kierstead, H. A. (2010) Planar graphs are 1-relaxed, 4-choosable. European J. Combin. 31 1385–1397.CrossRefGoogle Scholar
Dorbec, P., Kaiser, T., Montassier, M., and Raspaud, A. (2014) Limits of near-coloring of sparse graphs. J. Graph Theory 75 191–202.CrossRefGoogle Scholar
Dujmović, V. and Outioua, D. (2018) A note on defect-1 choosability of graphs on surfaces. arXiv:1806.06149Google Scholar
Dujmović, V., Sidiropoulos, A., and Wood, D. R. (2016) Layouts of expander graphs. Chicago J. Theoret. Comput. Sci. 2016 1.CrossRefGoogle Scholar
Dujmović, V. and Wood, D. R. (2004) On linear layouts of graphs. Discrete Math. Theor. Comput. Sci. 6 339–358.Google Scholar
Dvořák, Z. and Norin, S. (2017) Islands in minor-closed classes, I: Bounded treewidth and separators. arXiv:1710.02727Google Scholar
Dvořák, Z. and Postle, L. (2018) Correspondence coloring and its application to list-coloring planar graphs without cycles of lengths 4 to 8. J. Combin. Theory, Ser. B 129 38–54.CrossRefGoogle Scholar
Eaton, N. and Hull, T. (1999) Defective list colorings of planar graphs. Bull. Inst. Combin. Appl 25 79–87.Google Scholar
Edwards, K., Kang, D. Y., Kim, J., Oum, S.-I., and Seymour, P. (2015) A relative of Hadwiger’s conjecture. SIAM J. Discrete Math. 29 2385–2388.CrossRefGoogle Scholar
Esperet, L. and Ochem, P. (2016) Islands in graphs on surfaces. SIAM J. Discrete Math. 30 206–219.CrossRefGoogle Scholar
Gethner, E. and Sulanke, T. (2009) Thickness-two graphs, II: More new nine-critical graphs, independence ratio, cloned planar graphs, and singly and doubly outerplanar graphs. Graphs Combin. 25 197–217.CrossRefGoogle Scholar
Havet, F. and Sereni, J.-S. (2006) Improper choosability of graphs and maximum average degree. J. Graph Theory 52 181–199.CrossRefGoogle Scholar
Haxell, P. E. (2001) A note on vertex list colouring. Combin. Probab. Comput. 10 345–347.CrossRefGoogle Scholar
Haxell, P., Szabó, T., and Tardos, G. (2003) Bounded size components: Partitions and transversals. J. Combin. Theory Ser. B 88 281–297.CrossRefGoogle Scholar
van den Heuvel, J. and Wood, D. R. (2018) Improper colourings inspired by Hadwiger’s conjecture. J. London Math. Soc. 98 129–148.CrossRefGoogle Scholar
Hutchinson, J. P. (1993) Coloring ordinary maps, maps of empires and maps of the moon. Math. Mag. 66 211–226.CrossRefGoogle Scholar
Jackson, B. and Ringel, G. (2000) Variations on Ringel’s earth–moon problem. Discrete Math. 211 233–242.CrossRefGoogle Scholar
Kim, J., Kostochka, A., and Zhu, X. (2014) Improper coloring of sparse graphs with a given girth, I: (0,1)-colorings of triangle-free graphs. European J. Combin. 42 26–48.CrossRefGoogle Scholar
Kim, J., Kostochka, A., and Zhu, X. (2016) Improper coloring of sparse graphs with a given girth, II: Constructions. J. Graph Theory 81 403–413.CrossRefGoogle Scholar
Kopreski, M. and Yu, G. (2017) Maximum average degree and relaxed coloring. Discrete Math. 340 2528–2530.CrossRefGoogle Scholar
Liu, C.-H. and Oum, S.-I. (2017) Partitioning H-minor free graphs into three subgraphs with no large components. J. Combin. Theory Ser. B.Google Scholar
Lovász, L. (1966) On decomposition of graphs. Studia Sci. Math. Hungar. 1 237–238.Google Scholar
Mutzel, P., Odenthal, T., and Scharbrodt, M. (1998) The thickness of graphs: A survey. Graphs Combin. 14 59–73.CrossRefGoogle Scholar
Norin, S., Scott, A., Seymour, P., and Wood, D. R. (2017) Clustered colouring in minor-closed classes. (Norin, S., Scott, A., Seymour, P. and Wood, D. R.), Combinatorica, accepted in 2019. arXiv:1708.02370Google Scholar
Ossona de Mendez, P., Oum, S.-I., and Wood, D. R. (2018) Defective colouring of graphs excluding a subgraph or minor. Combinatorica. doi: 10.1007/s00493-018-3733-1CrossRefGoogle Scholar
Ringel, G. (1959) Färbungsprobleme auf Flächen und Graphen, Vol. 2 of Mathematische Monographien, VEB, Deutscher Verlag der Wissenschaften.Google Scholar
Wood, D. R. (2018) Defective and clustered graph colouring. Electron. J. Combin. #DS23.Google Scholar
Woodall, D. R. (2011) Defective choosability of graphs in surfaces. Discuss. Math. Graph Theory 31 441–459.CrossRefGoogle Scholar