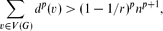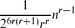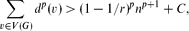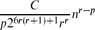Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cao, Shujuan
Dehmer, Matthias
and
Shi, Yongtang
2014.
Extremality of degree-based graph entropies.
Information Sciences,
Vol. 278,
Issue. ,
p.
22.
Gu, Ran
Li, Xueliang
and
Shi, Yongtang
2015.
Degree Powers in $$C_5$$ C 5 -Free Graphs.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 38,
Issue. 4,
p.
1627.
Chen, Zengqiang
Dehmer, Matthias
and
Shi, Yongtang
2015.
Bounds for degree-based network entropies.
Applied Mathematics and Computation,
Vol. 265,
Issue. ,
p.
983.
Cao, Shujuan
and
Dehmer, Matthias
2015.
Degree-based entropies of networks revisited.
Applied Mathematics and Computation,
Vol. 261,
Issue. ,
p.
141.
Chen, Zengqiang
Dehmer, Matthias
Emmert-Streib, Frank
and
Shi, Yongtang
2015.
Entropy of Weighted Graphs with Randi´c Weights.
Entropy,
Vol. 17,
Issue. 6,
p.
3710.
Li, Xueliang
and
Wei, Meiqin
2016.
Mathematical Foundations and Applications of Graph Entropy.
p.
133.
Lan, Yongxin
Liu, Henry
Qin, Zhongmei
and
Shi, Yongtang
2019.
Degree powers in graphs with a forbidden forest.
Discrete Mathematics,
Vol. 342,
Issue. 3,
p.
821.
Zhang, Liwen
2022.
Degree powers in K,-minor free graphs.
Discrete Mathematics,
Vol. 345,
Issue. 4,
p.
112783.
Gerbner, Dániel
Nagy, Zoltán Lóránt
and
Vizer, Máté
2022.
Unified approach to the generalized Turán problem and supersaturation.
Discrete Mathematics,
Vol. 345,
Issue. 3,
p.
112743.
Dong, Yanni
Gadouleau, Maximilien
Wan, Pengfei
and
Zhang, Shenggui
2024.
Graphs with minimum degree-entropy.
Information Sciences,
Vol. 671,
Issue. ,
p.
120629.
Gerbner, Dániel
2025.
On degree powers and counting stars in F-free graphs.
European Journal of Combinatorics,
Vol. 126,
Issue. ,
p.
104135.
Gao, Jun
Liu, Xizhi
Ma, Jie
and
Pikhurko, Oleg
2025.
Phase Transition of Degenerate Turán Problems in \({p}\)-Norms.
SIAM Journal on Discrete Mathematics,
Vol. 39,
Issue. 3,
p.
1712.
Ren, Yuhe
and
Wu, Baoyindureng
2025.
The outdegree power of oriented graphs.
Computational and Applied Mathematics,
Vol. 44,
Issue. 1,