Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T22:38:49.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree Ramsey Numbers of Graphs

Published online by Cambridge University Press:  02 February 2012

WILLIAM B. KINNERSLEY ,
KEVIN G. MILANS  and
DOUGLAS B. WEST
WILLIAM B. KINNERSLEY
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA (e-mail: wkinner2@illinois.edu, west@math.uiuc.edu)
KEVIN G. MILANS
Affiliation:
Mathematics Department, University of South Carolina, USA (e-mail: milans@math.sc.edu)
DOUGLAS B. WEST
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA (e-mail: wkinner2@illinois.edu, west@math.uiuc.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H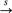G mean that every s-colouring of E(H) produces a monochromatic copy of G in some colour class. Let the s-colour degree Ramsey number of a graph G, written RΔ(G; s), be min{Δ(H): H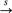G}. If T is a tree in which one vertex has degree at most k and all others have degree at most ⌈k/2⌉, then RΔ(T; s) = s(k − 1) + ϵ, where ϵ = 1 when k is odd and ϵ = 0 when k is even. For general trees, RΔ(T; s) ≤ 2s(Δ(T) − 1).

To study sharpness of the upper bound, consider the double-starSa,b, the tree whose two non-leaf vertices have degrees a and b. If a ≤ b, then RΔ(Sa,b; 2) is 2b − 2 when a < b and b is even; it is 2b − 1 otherwise. If s is fixed and at least 3, then RΔ(Sb,b;s) = f(s)(b − 1) − o(b), where f(s) = 2s − 3.5 − O(s−1).

We prove several results about edge-colourings of bounded-degree graphs that are related to degree Ramsey numbers of paths. Finally, for cycles we show that RΔ(C2k + 1; s) ≥ 2s + 1, that RΔ(C2k; s) ≥ 2s, and that RΔ(C4;2) = 5. For the latter we prove the stronger statement that every graph with maximum degree at most 4 has a 2-edge-colouring such that the subgraph in each colour class has girth at least 5.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 229 - 253
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. (1996) Bipartite subgraphs. Combinatorica 16 301–311.CrossRefGoogle Scholar
[2]Alon, N., Ding, G., Oporowski, B. and Vertigan, D. (2003) Partitioning into graphs with only small components. J. Combin. Theory Ser. B 87 231–243.CrossRefGoogle Scholar
[3]Beck, J. (1983) On size Ramsey number of paths, trees and cycles I. J. Graph Theory 7 115–130.CrossRefGoogle Scholar
[4]Beck, J. (1990) On size Ramsey number of paths, trees and cycles II. In Mathematics of Ramsey Theory, Vol. 5 of Algorithms and Combinatorics, Springer, pp. 34–45.CrossRefGoogle Scholar
[5]Beineke, L. W. and Schwenk, A. J. (1975) On a bipartite form of the Ramsey problem. Congress. Numer. 15 17–22.Google Scholar
[6]Bollobás, B., Saito, A. and Wormald, N. C. (1985) Regular factors of regular graphs. J. Graph Theory 9 97–103.CrossRefGoogle Scholar
[7]Brooks, R. L. (1941) On colouring the nodes of a network. Proc. Cambridge Philos. Soc. 37 194–197.CrossRefGoogle Scholar
[8]Burr, S., Erdős, P. and Lovász, L. (1976) On graphs of Ramsey type. Ars Combinatoria 1 167–190.Google Scholar
[9]Carnielli, W. A. and Monte Carmelo, E. L. (1999) On the Ramsey problem for multicolor bipartite graphs. Adv. Appl. Math. 22 48–59.CrossRefGoogle Scholar
[10]Donadelli, J., Haxell, P. E. and Kohayakawa, Y. (2005) A note on the size-Ramsey number of long subdivisions of graphs. RAIRO-Inf. Theor. Appl. 39 191–206.CrossRefGoogle Scholar
[11]Egawa, Y., Urabe, M., Fukuda, T. and Nagoya, S. (1986) A decomposition of complete bipartite graphs into edge-disjoint subgraphs with star components. Discrete Math. 58 93–95.CrossRefGoogle Scholar
[12]Erdős, P., Faudree, R. J., Rousseau, C. C. and Schelp, R. H. (1978) The size Ramsey number. Period. Math. Hungar. 9 145–161.CrossRefGoogle Scholar
[13]Erdős, P. and Sachs, H. (1963) Reguläre Graphen gegebener Taillenweite mit minimaler Knotenzahl (in German). Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe 12 251–257.Google Scholar
[14]Folkman, J. (1970) Graphs with monochromatic complete subgraphs in every edge coloring. SIAM J. Appl. Math. 18 19–24.CrossRefGoogle Scholar
[15]Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7 71–76.CrossRefGoogle Scholar
[16]Harary, F., Hsu, D. and Miller, Z. (1977) The biparticity of a graph. J. Graph Theory 1 131–133.CrossRefGoogle Scholar
[17]Jiang, T., Milans, K. G. and West, D. B. Degree Ramsey numbers for cycles and blowups of trees, submitted.Google Scholar
[18]Lubotzky, A., Phillips, R. and Sarnak, P. (1986) Explicit expanders, and the Ramanujan conjectures. In Proc. 18th ACM STOC, pp. 240–246.CrossRefGoogle Scholar
[19]Morgenstern, M. (1994) Existence and explicit constructions of (q + 1)-regular Ramanujan graphs for every prime power q. J. Combin. Theory Ser. B 62 44–62.CrossRefGoogle Scholar
[20]Nash-Williams, C. St. J. A. (1964) Decomposition of a finite graph into forests. J. London Math. Soc. 39 12.CrossRefGoogle Scholar
[21]Nešetřil, J. and Rödl, V. (1976) The Ramsey property for graphs with forbidden complete subgraphs. J. Combin. Theory Ser. B 20 243–249.CrossRefGoogle Scholar
[22]Petersen, J. (1891) Die Theorie der regulären Graphen. Acta Math. 15 193–220.CrossRefGoogle Scholar
[23]Ramsey, F. P. (1930) On a problem of formal logic. Proc. Lond. Math. Soc. 30 264–286.CrossRefGoogle Scholar
[24]Rödl, V. and Szemerédi, E. (2000) On size Ramsey numbers of graphs with bounded maximum degree. Combinatorica 20 257–262.Google Scholar
[25]Thomassen, C. (1999) Two-coloring the edges of a cubic graph such that each monochromatic component is a path of length at most 5. J. Combin. Theory Ser. B 75 100–109.CrossRefGoogle Scholar
[26]Vizing, V. G. (1964) On an estimate of the chromatic class of a p-graph. Diskret. Anal. 3 25–30.Google Scholar
[27]Zhu, X. (1998) Chromatic Ramsey numbers. Discrete Math. 190 215–222.CrossRefGoogle Scholar
[28]Zhu, X. (2011) The fractional version of Hedetniemi's conjecture is true. European J. Combin. 32 1168–1175.CrossRefGoogle Scholar