Article contents
Diameters in Supercritical Random Graphs Via First Passage Percolation
Published online by Cambridge University Press: 05 October 2010
Abstract
We study the diameter of 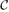 1, the largest component of the Erdős–Rényi random graph
1, the largest component of the Erdős–Rényi random graph 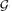 (n, p) in the emerging supercritical phase, i.e., for p =
(n, p) in the emerging supercritical phase, i.e., for p = 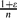 where ε3n → ∞ and ε = o(1). This parameter was extensively studied for fixed ε > 0, yet results for ε = o(1) outside the critical window were only obtained very recently. Prior to this work, Riordan and Wormald gave precise estimates on the diameter; however, these did not cover the entire supercritical regime (namely, when ε3n → ∞ arbitrarily slowly). Łuczak and Seierstad estimated its order throughout this regime, yet their upper and lower bounds differed by a factor of
where ε3n → ∞ and ε = o(1). This parameter was extensively studied for fixed ε > 0, yet results for ε = o(1) outside the critical window were only obtained very recently. Prior to this work, Riordan and Wormald gave precise estimates on the diameter; however, these did not cover the entire supercritical regime (namely, when ε3n → ∞ arbitrarily slowly). Łuczak and Seierstad estimated its order throughout this regime, yet their upper and lower bounds differed by a factor of 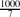 .
.
We show that throughout the emerging supercritical phase, i.e., for any ε = o(1) with ε3n → ∞, the diameter of 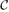 1 is with high probability asymptotic to D(ε, n) = (3/ε)log(ε3n). This constitutes the first proof of the asymptotics of the diameter valid throughout this phase. The proof relies on a recent structure result for the supercritical giant component, which reduces the problem of estimating distances between its vertices to the study of passage times in first-passage percolation. The main advantage of our method is its flexibility. It also implies that in the emerging supercritical phase the diameter of the 2-core of
1 is with high probability asymptotic to D(ε, n) = (3/ε)log(ε3n). This constitutes the first proof of the asymptotics of the diameter valid throughout this phase. The proof relies on a recent structure result for the supercritical giant component, which reduces the problem of estimating distances between its vertices to the study of passage times in first-passage percolation. The main advantage of our method is its flexibility. It also implies that in the emerging supercritical phase the diameter of the 2-core of 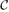 1 is w.h.p. asymptotic to
1 is w.h.p. asymptotic to 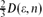 , and the maximal distance in
, and the maximal distance in 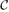 1 between any pair of kernel vertices is w.h.p. asymptotic to
1 between any pair of kernel vertices is w.h.p. asymptotic to 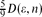 .
.
Information
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 729 - 751
- Copyright
- Copyright © Cambridge University Press 2010
References
- 20
- Cited by

