Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T23:21:55.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Distinct Distances on Algebraic Curves in the Plane

Published online by Cambridge University Press:  15 July 2016

JÁNOS PACH  and
FRANK DE ZEEUW
JÁNOS PACH
Affiliation:
Department of Mathematics, EPFL, Lausanne, Switzerland and Rényi Institute, Budapest, Hungary (e-mail: pach@cims.nyu.edu)
FRANK DE ZEEUW
Affiliation:
Department of Mathematics, EPFL, Lausanne, Switzerland (e-mail: fdezeeuw@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

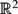Let S be a set of n points in ${\mathbb R}^{2}$ contained in an algebraic curve C of degree d. We prove that the number of distinct distances determined by S is at least cdn4/3, unless C contains a line or a circle.

We also prove the lower bound cd′ min{m2/3n2/3, m2, n2} for the number of distinct distances between m points on one irreducible plane algebraic curve and n points on another, unless the two curves are parallel lines, orthogonal lines, or concentric circles. This generalizes a result on distances between lines of Sharir, Sheffer and Solymosi in [19].

Keywords

Primary 52C10Secondary 52C45
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 1 , January 2017 , pp. 99 - 117
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barone, S. and Basu, S. (2016) On a real analogue of Bezout inequality and the number of connected components of sign conditions. Proc. London Math. Soc. 112 115–145.CrossRefGoogle Scholar
[2] Basu, S., Pollack, P. and Roy, M.-F. (2006) Algorithms in Real Algebraic Geometry, Springer.Google Scholar
[3] Brass, P., Moser, W. and Pach, J. (2005) Research Problems in Discrete Geometry, Springer.Google Scholar
[4] Charalambides, M. (2014) Exponent gaps on curves via rigidity. Discrete Comput. Geom. 51 666–701.Google Scholar
[5] Cox, D., Little, J. and O'Shea, D. (2007) Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, Springer.CrossRefGoogle Scholar
[6] Elekes, G. (1999) A note on the number of distinct distances. Period. Math. Hung. 38 173–301.Google Scholar
[7] Elekes, G. and Rónyai, L. (2000) A combinatorial problem on polynomials and rational functions. J. Combin. Theory Ser. A 89 1–20.Google Scholar
[8] Elekes, G and Sharir, M. (2011) Incidences in three dimensions and distinct distances in the plane. Combin. Probab. Comput. 20 571–608.CrossRefGoogle Scholar
[9] Erdős, P. (1946) On sets of distances of n points. Amer. Math. Monthly 53 248–250.Google Scholar
[10] Gibson, C. (1998) Elementary Geometry of Algebraic Curves, Cambridge University Press.Google Scholar
[11] Guth, L. and Katz, N. H. (2015) On the Erdős distinct distances problem in the plane. Ann. of Math. 181 155–190.Google Scholar
[12] Harris, J. (1992) Algebraic Geometry: A First Course, Springer.Google Scholar
[13] Heintz, J. (1983) Definability and fast quantifier elimination in algebraically closed fields. Theoret. Comput. Sci. 24 239–277.Google Scholar
[14] Kaplan, H., Matoušek, J. and Sharir, M. (2012) Simple proofs of classical theorems in discrete geometry via the Guth–Katz polynomial partitioning technique. Discrete Comput. Geom. 48 499–517.CrossRefGoogle Scholar
[15] Pach, J. and Sharir, M. (1992) Repeated angles in the plane and related problems. J. Combin. Theory Ser. A 59 12–22.CrossRefGoogle Scholar
[16] Pach, J. and Sharir, M. (1998) On the number of incidences between points and curves. Combin. Probab. Comput. 7 121–127.Google Scholar
[17] Raz, O. E., Sharir, M. and Solymosi, J. (2014) Polynomials vanishing on grids: The Elekes–Rónyai problem revisited. In SOCG'14: Proceedings of the 30th Annual Symposium on Computational Geometry, pp. 198–205.Google Scholar
[18] Schwartz, R., Solymosi, J. and de Zeeuw, F. (2013) Extensions of a result of Elekes and Rónyai. J. Combin. Theory Ser. A 120 1695–1713.CrossRefGoogle Scholar
[19] Sharir, M., Sheffer, A. and Solymosi, J. (2013) Distinct distances on two lines. J. Combin. Theory Ser. A 120 1732–1736.Google Scholar
[20] Sharir, M. and Solymosi, J. (2016) Distinct distances from three points. Combin. Probab. Comput. 25 623–632.Google Scholar
[21] Sheffer, A., Zahl, J. and de Zeeuw, F. (2014) Few distinct distances implies no heavy lines or circles. Combinatorica, to appear. doi:10.1007/s00493-014-3180-6 Google Scholar
[22] Solymosi, J. and Tao, T. (2012) An incidence theorem in higher dimensions. Discrete Comput. Geom. 48 255–280.Google Scholar