Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T02:39:55.512Z Has data issue: false hasContentIssue false
  • English
  • Français

The Distribution of Heights of Binary Trees and Other Simple Trees

Published online by Cambridge University Press:  12 September 2008

Philippe Flajolet ,
Zhicheng Gao ,
Andrew Odlyzko  and
Bruce Richmond
Philippe Flajolet
Affiliation:
INRIA, 78150 Rocquencourt, France
Zhicheng Gao
Affiliation:
Dept. of Mathematics and Statistics, Carleton University, Ottawa, Ontario K1S5B6, Canada
Andrew Odlyzko
Affiliation:
AT& T Bell Laboratories, Murray Hill, New Jersey 07974, United States
Bruce Richmond
Affiliation:
Dept. of Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, N2L3G1, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

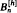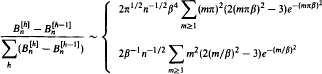
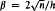The number, , of rooted plane binary trees of height ≤ h with n internal nodes is shown to satisfy

uniformly for δ−1(log n)−1/2 ≤ β ≤ δ(log n)1/2, where and δ is a positive constant. An asymptotic formula for 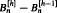is derived for 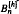h = cn, where 0 < c < 1. Bounds for are also derived for large and small heights. The methods apply to any simple family of trees, and the general asymptotic results are stated.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 2 , Issue 2 , June 1993 , pp. 145 - 156
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bender, E. A. and Richmond, L. B. (1983) Central and local limit theorems applied to asymptotic enumeration II: Multivariate generating functions. J. Combin. Theory Ser. B 34 255–265.CrossRefGoogle Scholar
[2]Brown, G. G. and Shubert, B. O. (1984) On random binary trees. Math. Oper. Res. 9 43–65.CrossRefGoogle Scholar
[3]de Bruijn, N. (1961) Asymptotic Methods in Analysis, North-Holland, Amsterdam.Google Scholar
[4]de Bruijn, N., Knuth, D. and Rice, S. (1972) The average height of planted plane trees. In: Read, R. C. (ed.) Graph Theory and Computing, Academic Press, New York15–22.CrossRefGoogle Scholar
[5]Flajolet, P. and Odlyzko, A. M. (1982) The average height of binary trees and other simple Trees. J. Comp. Sys. Sci. 25 171–213.CrossRefGoogle Scholar
[6]Kolchin, V. F. (1986) Random Mappings, (English translation of 1984 Russian original), Optimization Software.Google Scholar
[7]Luczak, T. (preprint) The number of trees with a large diameter.Google Scholar
[8]Meir, A. and Moon, J. W. (1978) On the altitude of nodes in random trees. Canad. J. Math. 30 997–1015.CrossRefGoogle Scholar
[9]Odlyzko, A. (1982) Periodic oscillation of coefficients of power series that satisfy functional equations. Adv. in Math. 44 180–205.CrossRefGoogle Scholar
[10]Rényi, A. and Szekeres, G. (1967) On the height of trees. Aust. J. Math. 7 497–507.CrossRefGoogle Scholar
[11]Szekeres, G. (1958) Regular iteration of real and complex functions. Acta Math. 100 203–258.CrossRefGoogle Scholar
[12]Wimp, J. (1991) Current trends in asymptotics: some problems and some solutions. J. Comp. and Appl. Math. 35 53–79.CrossRefGoogle Scholar
[13]Wright, R. A., Richmond, B., Odlyzko, A. and Mckay, B. D. (1986) Constant time generation of free trees. SIAM. J. Comput. 15 540–548.CrossRefGoogle Scholar