Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T22:09:16.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues and triangles in graphs

Part of: Graph theory

Published online by Cambridge University Press:  28 September 2020

Huiqiu Lin ,
Bo Ning  and
Baoyindureng Wu
Huiqiu Lin
Affiliation:
Department of Mathematics, East China University of Science and Technology, Shanghai200237, PR China
Bo Ning*
Affiliation:
College of Computer Science, Nankai University, Tianjin300071, PR China
Baoyindureng Wu
Affiliation:
College of Mathematics and System Science, Xinjiang University, Urumqi, Xinjiang830046, PR China
*
*Corresponding author. Email: bo.ning@nankai.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Bollobás and Nikiforov (J. Combin. Theory Ser. B.97 (2007) 859–865) conjectured the following. If G is a Kr+1-free graph on at least r+1 vertices and m edges, then ${\rm{\lambda }}_1^2(G) + {\rm{\lambda }}_2^2(G) \le (r - 1)/r \cdot 2m$, where λ1 (G)and λ2 (G) are the largest and the second largest eigenvalues of the adjacency matrix A(G), respectively. In this paper we confirm the conjecture in the case r=2, by using tools from doubly stochastic matrix theory, and also characterize all families of extremal graphs. Motivated by classic theorems due to Erdös and Nosal respectively, we prove that every non-bipartite graph of order and size contains a triangle if one of the following is true: (i) ${{\rm{\lambda }}_1}(G) \ge \sqrt {m - 1} $ and 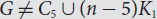$G \ne {C_5} \cup (n - 5){K_1}$, and (ii) 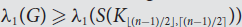${{\rm{\lambda }}_1}(G) \ge {{\rm{\lambda }}_1}(S({K_{[(n - 1)/2],[(n - 1)/2]}}))$ and 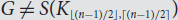$G \ne S({K_{[(n - 1)/2],[(n - 1)/2]}})$, where $S({K_{[(n - 1)/2],[(n - 1)/2]}})$ is obtained from ${K_{[(n - 1)/2],[(n - 1)/2]}}$ by subdividing an edge. Both conditions are best possible. We conclude this paper with some open problems.

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 258 - 270
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by NSFC (grants 11771141 and 12011530064).

‡

This work is supported by NSFC (No. 11971346).

§

Research supported by NSFC (grant 11571294).

References

Alon, N. (1986) Eigenvalues and expanders. Combinatorica 6 83–96.CrossRefGoogle Scholar
Alon, N. (1996) Bipartite subgraphs. Combinatorica 16 301–311.CrossRefGoogle Scholar
Ando, T. and Lin, M. (2015) Proof of a conjectured lower bound on the chromatic number of a graph. Linear Algebra Appl. 485 480–484.CrossRefGoogle Scholar
Andrásfai, B., Erdös, P. and Sós, V. T. (1974) On the connection between chromatic number, maximal clique and minimal degree of a graph. Discrete Math. 8 205–218.CrossRefGoogle Scholar
Benzaken, C. and Hammer, P. L. (1978) Linear separation of dominating sets in graphs. Ann. Discrete Math. 3 1–10.CrossRefGoogle Scholar
Bollobás, B. and Nikiforov, V. (2007) Cliques and the spectral radius. J. Combin. Theory Ser. B 97 859–865.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R. (2008) Graph Theory, Vol. 244 of Graduate Texts in Mathematics. Springer.CrossRefGoogle Scholar
Brouwer, A. E. and Haemers, W. H. (2005) Eigenvalues and perfect matchings. Linear Algebra Appl. 395 155–162.CrossRefGoogle Scholar
Brualdi, R. A. and Hoffman, A. J. (1985) On the spectral radius of (0, 1)-matrices. Linear Algebra Appl. 65 133–146.CrossRefGoogle Scholar
Chung, F. (1989) Diameters and eigenvalues. J. Amer. Math. Soc. 2 187–196.CrossRefGoogle Scholar
Cioabă, S. M., van Dam, E. R., Koolen, J. H. and Lee, J. H. (2010) A lower bound for the spectral radius of graphs with fixed diameter. European J. Combin. 31 1560–1566.CrossRefGoogle Scholar
Cioabă, S. M., Gregory, D. A. and Haemers, W. H. (2009) Matchings in regular graphs from eigenvalues. J. Combin. Theory Ser. B 99 287–297.CrossRefGoogle Scholar
Cvetković, D., Doob, M. and Sachs, H. (1980) Spectra of Graphs: Theory and Application, Vol. 87 of Pure and Applied Mathematics. Academic Press.Google Scholar
Edwards, C. and Elphick, C. (1983) Lower bounds for the clique and the chromatic number of a graph. Discrete Appl. Math. 5 51–64.CrossRefGoogle Scholar
Elphick, C., Farber, M., Goldberg, F. and Wocjan, P. (2016) Conjectured bounds for the sum of squares of positive eigenvalues of a graph. Discrete Math. 339 2215–2223.CrossRefGoogle Scholar
Feng, L. H., Zhang, P. L. and Liu, W. J. (2018) Spectral radius and k-connectedness of a graph. Monatsh. Math. 185 651–661.CrossRefGoogle Scholar
Heuvel, J. V. (1995) Hamilton cycles and eigenvalues of graphs. Linear Algebra Appl. 226–228 723–730.CrossRefGoogle Scholar
Hoffman, A. J. and Smith, J. H. (1975) On the spectral radii of topologically equivalent graphs. In Recent Advances in Graph Theory (Fiedler, M., ed.), pp. 273–281. Academia Praha.Google Scholar
Hong, Y. (1988) Bounds of eigenvalues of a graph. Acta Math. Appl. Sinica (English Ser.) 4 165–168.CrossRefGoogle Scholar
Hong, Y. (1993) Bounds of eigenvalues of graphs. Discrete Math. 123 65–74.CrossRefGoogle Scholar
Hong, Y., Shu, J. L. and Fang, K. F. (2001) A sharp upper bound of the spectral radius of graphs. J. Combin. Theory Ser. B 81 177–183.CrossRefGoogle Scholar
Kuang, J. C. (2003) Changyong Budengshi [Applied Inequalities] (in Chinese), third section. Shandong Kexue Jishu Chubanshe.Google Scholar
Li, B. L. and Ning, B. (2016) Spectral analogues of Erdös’ and Moon–Moser’s theorems on Hamilton cycles. Linear Multilinear Algebra 64 2252–2269.CrossRefGoogle Scholar
Liu, B., Shen, J. and Wang, X. (2007) On the largest eigenvalue of non-regular graphs. J. Combin. Theory Ser. B 97 1010–1018.CrossRefGoogle Scholar
Liu, M. H., Lai, H. J. and Das, K. C. (2019) Spectral results on Hamiltonian problem. Discrete Math. 342 1718–1730.CrossRefGoogle Scholar
Lu, H. L. (2012) Regular graphs, eigenvalues and regular factors. J. Graph Theory 69 349–355.CrossRefGoogle Scholar
Motzkin, T. and Straus, E. (1965) Maxima for graphs and a new proof of a theorem of Turán. Canad. J. Math. 17 533–540.CrossRefGoogle Scholar
Nikiforov, V. (2002) Some inequalities for the largest eigenvalue of a graph. Combin. Probab. Comput. 11 179–189.CrossRefGoogle Scholar
Nikiforov, V. (2006) Walks and spectral radius of graphs. Linear Algebra Appl. 418 257–268.CrossRefGoogle Scholar
Nikiforov, V. (2009) More spectral bounds on the clique and independence numbers. J. Combin. Theory Ser. B 99 819–826.CrossRefGoogle Scholar
Nikiforov, V. (2009) The maximum spectral radius of C 4-free graphs of given order and size. Linear Algebra Appl. 430 2898–2905.CrossRefGoogle Scholar
Nikiforov, V. (2011) Some new results in extremal graph theory. In Surveys in Combinatorics 2011, Vol 392 of London Mathematical Society Lecture Note Series, pp. 141–181. Cambridge University Press.CrossRefGoogle Scholar
Nosal, E. (1970) Eigenvalues of graphs. Master’s thesis, University of Calgary.Google Scholar
Oboudi, M. R. (2016) Bipartite graphs with at most six non-zero eigenvalues. Ars Math. Contemp. 11 315–325.CrossRefGoogle Scholar
Stanley, R. P. (1987) A bound on the spectral radius of graphs with e edges. Linear Algebra Appl. 87 267–269.CrossRefGoogle Scholar
Tait, M. and Tobin, J. (2017) Three conjectures in extremal spectral graph theory. J. Combin. Theory Ser. B 126 137–161.CrossRefGoogle Scholar
Wilf, H. (1986) Spectral bounds for the clique and independence numbers of graphs. J. Combin. Theory Ser. B 40 113–117.CrossRefGoogle Scholar
Zhai, M. Q., Lin, H. Q. and Shu, J. In preparation.Google Scholar
Zhan, X. (2013) Matrix Theory, Vol. 147 of Graduate Studies in Mathematics. American Mathematical Society.CrossRefGoogle Scholar
Zhou, B. and Cho, H. H. (2005) Remarks on spectral radius and Laplacian eigenvalues of a graph. Czechoslovak Math. J. 55 781–790.CrossRefGoogle Scholar