Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:55:45.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Finding tight Hamilton cycles in random hypergraphs faster

Part of: Graph theory

Published online by Cambridge University Press:  23 September 2020

Peter Allen ,
Christoph Koch ,
Olaf Parczyk  and
Yury Person
Peter Allen
Affiliation:
Department of Mathematics, London School of Economics, Houghton Street, London WC2A 2AE, UK
Christoph Koch
Affiliation:
Department of Statistics, University of Oxford, St Giles 24–29, Oxford OX1 3LB, UK
Olaf Parczyk*
Affiliation:
Department of Mathematics, London School of Economics, Houghton Street, London WC2A 2AE, UK
Yury Person
Affiliation:
Institut für Mathematik, Technische Universität Ilmenau, 98684 Ilmenau, Germany
*
*Corresponding author. Email: o.parczyk@lse.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In an r-uniform hypergraph on n vertices, a tight Hamilton cycle consists of n edges such that there exists a cyclic ordering of the vertices where the edges correspond to consecutive segments of r vertices. We provide a first deterministic polynomial-time algorithm, which finds a.a.s. tight Hamilton cycles in random r-uniform hypergraphs with edge probability at least C log3n/n.

Our result partially answers a question of Dudek and Frieze, who proved that tight Hamilton cycles exist already for p = ω(1/n) for r = 3 and p = (e + o(1))/n for 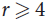$r \ge 4$ using a second moment argument. Moreover our algorithm is superior to previous results of Allen, Böttcher, Kohayakawa and Person, and Nenadov and Škorić, in various ways: the algorithm of Allen et al. is a randomized polynomial-time algorithm working for edge probabilities 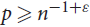$p \ge {n^{ - 1 + \varepsilon}}$, while the algorithm of Nenadov and Škorić is a randomized quasipolynomial-time algorithm working for edge probabilities 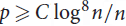$p \ge C\mathop {\log }\nolimits^8 n/n$.

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05C80: Random graphs 05C85: Graph algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 239 - 257
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The second author was supported by Austrian Science Fund (FWF), P26826, and European Research Council (ERC), no. 639046.

‡

The third and fourth authors were supported by DFG grant PE 2299/1-1.

References

Allen, P., Böttcher, J., Kohayakawa, Y. and Person, Y. (2015) Tight Hamilton cycles in random hypergraphs. Random Struct. Algorithms 46 446–465.CrossRefGoogle Scholar
Angluin, D. and Valiant, L. G. (1979) Fast probabilistic algorithms for Hamiltonian circuits and matchings. J. Comput. System Sci. 18 155–193.CrossRefGoogle Scholar
Björklund, A. (2014) Determinant sums for undirected Hamiltonicity. SIAM J. Comput. 43 280–299.CrossRefGoogle Scholar
Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics (Cambridge, 1983), pp. 35–57. Academic Press.Google Scholar
Bollobás, B., Fenner, T. I. and Frieze, A. (1987) An algorithm for finding Hamilton paths and cycles in random graphs. Combinatorica 7 327–341.CrossRefGoogle Scholar
Clemens, D., Ehrenmüller, J. and Person, Y. (2016) A Dirac-type theorem for Hamilton Berge cycles in random hypergraphs. Electron. Notes Discrete Math. 54 181–186.CrossRefGoogle Scholar
Dudek, A. and Frieze, A. (2011) Loose Hamilton cycles in random uniform hypergraphs. Electron. J. Combin. 18 #48.CrossRefGoogle Scholar
Dudek, A. and Frieze, A. (2013) Tight Hamilton cycles in random uniform hypergraphs. Random Struct. Algorithms 42 374–385.CrossRefGoogle Scholar
Friedgut, E. (1999) Sharp thresholds of graph properties, and the k-sat problem. J. Amer. Math. Soc. 12 1017–1054.CrossRefGoogle Scholar
Frieze, A. (2010) Loose Hamilton cycles in random 3-uniform hypergraphs. Electron. J. Combin. 17 Note 28.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs. Wiley-Interscience.CrossRefGoogle Scholar
Johansson, A., Kahn, J. and Vu, V. (2008) Factors in random graphs. Random Struct. Algorithms 33 1–28.CrossRefGoogle Scholar
Karp, R. M. (1972) Reducibility among combinatorial problems. In Complexity of Computer Computations (Miller, R. E. et al., eds), The IBM Research Symposia Series, pp. 85–103. Springer.CrossRefGoogle Scholar
Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.CrossRefGoogle Scholar
Korshunov, A. (1976) Solution of a problem of Erdös and Rényi on Hamiltonian cycles in nonoriented graphs. Sov. Math. Dokl. 17 760–764.Google Scholar
Korshunov, A. (1977) Solution of a problem of P. Erdös and A. Rényi on Hamiltonian cycles in undirected graphs. Metody Diskretn. Anal. 31 17–56.Google Scholar
Krivelevich, M. (1997) Triangle factors in random graphs. Combin. Probab. Comput. 6 337–347.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2012) On Pósa’s conjecture for random graphs. SIAM J. Discrete Math. 26 1440–1457.CrossRefGoogle Scholar
Montgomery, R. (2014) Embedding bounded degree spanning trees in random graphs. arXiv:1405.6559v2Google Scholar
Montgomery, R. (2019) Spanning trees in random graphs. Adv. Math. 356 106793.CrossRefGoogle Scholar
Nenadov, R. and Škorić, N. (2019) Powers of Hamilton cycles in random graphs and tight Hamilton cycles in random hypergraphs. Random Struct. Algorithms 54 187–208.CrossRefGoogle Scholar
Poole, D. (2014) On weak Hamiltonicity of a random hypergraph. arXiv:1410.7446Google Scholar
Pósa, L. (1976) Hamiltonian circuits in random graphs. Discrete Math. 14 359–364.CrossRefGoogle Scholar
Riordan, O. (2000) Spanning subgraphs of random graphs. Combin. Probab. Comput. 9 125–148.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2006) A Dirac-type theorem for 3-uniform hypergraphs. Combin. Probab. Comput. 15 229–251.CrossRefGoogle Scholar
Shamir, E. (1983) How many random edges make a graph Hamiltonian? Combinatorica 3 123–131.CrossRefGoogle Scholar