Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T21:31:34.479Z Has data issue: false hasContentIssue false
  • English
  • Français

First Passage Percolation on the Erdős–Rényi Random Graph

Published online by Cambridge University Press:  20 June 2011

SHANKAR BHAMIDI ,
REMCO VAN DER HOFSTAD  and
GERARD HOOGHIEMSTRA
SHANKAR BHAMIDI
Affiliation:
Department of Statistics and Operations Research, 304 Hanes Hall, University of North Carolina, Chapel Hill, NC 27599, USA (e-mail: bhamidi@email.unc.edu)
REMCO VAN DER HOFSTAD
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands (e-mail: rhofstad@win.tue.nl)
GERARD HOOGHIEMSTRA
Affiliation:
DIAM, Delft University of Technology, Mekelweg 4, 2628CD Delft, The Netherlands (e-mail: g.hooghiemstra@tudelft.nl)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we explore first passage percolation (FPP) on the Erdős–Rényi random graph Gn(pn), where we assign independent random weights, having an exponential distribution with rate 1, to the edges. In the sparse regime, i.e., when npn → λ > 1, we find refined asymptotics both for the minimal weight of the path between uniformly chosen vertices in the giant component, as well as for the hopcount (i.e., the number of edges) on this minimal weight path. More precisely, we prove a central limit theorem for the hopcount, with asymptotic mean and variance both equal to (λ log n)/(λ − 1). Furthermore, we prove that the minimal weight centred by (log n)/(λ − 1) converges in distribution.

We also investigate the dense regime, where npn → ∞. We find that although the base graph is ultra-small (meaning that graph distances between uniformly chosen vertices are o(log n)), attaching random edge weights changes the geometry of the network completely. Indeed, the hopcount Hn satisfies the universality property that whatever the value of pn, Hn/log n → 1 in probability and, more precisely, (Hn − βn log n)/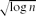, where βn = λn/(λn − 1), has a limiting standard normal distribution. The constant βn can be replaced by 1 precisely when λn ≫ 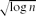, a case that has appeared in the literature (under stronger conditions on λn) in [4, 13]. We also find lower bounds for the maximum, over all pairs of vertices, of the optimal weight and hopcount.

This paper continues the investigation of FPP initiated in [4] and [5]. Compared to the setting on the configuration model studied in [5], the proofs presented here are much simpler due to a direct relation between FPP on the Erdős–Rényi random graph and thinned continuous-time branching processes.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 5 , September 2011 , pp. 683 - 707
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Amini, H. (2011) Epidemics and percolation in random networks. PhD thesis, ENS Inria Rocquencourt.Google Scholar
[2]Amini, H., Draief, M. and Lelarge, M. (2010) Flooding in weighted random graphs. Preprint. arxiv.org/abs/1011.5994Google Scholar
[3]Athreya, K. B. and Ney, P. E. (2004) Branching Processes, Dover.Google Scholar
[4]Bhamidi, S. (2008) First passage percolation on locally tree like networks I: Dense random graphs. J. Math. Phys. 49 125218.CrossRefGoogle Scholar
[5]Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2010) First passage percolation on random graphs with finite mean degrees. Ann. Appl. Probab. 20 1907–1965.CrossRefGoogle Scholar
[6]Billingsley, P. (1999) Convergence of Probability Measures, second edition, Wiley-Interscience.CrossRefGoogle Scholar
[7]Bühler, W. J. (1971) Generations and degree of relationship in supercritical Markov branching processes. Probab. Theory Rel. Fields 18 141–152.Google Scholar
[8]Chen, L. H. Y. and Shao, Q. M. (2005) Stein's method for normal approximation. In An Introduction to Stein's Method (Barbour, A. D. and Chen, L. H. Y., eds), IMS Lecture Note Series, National University of Singapore, pp. 1–59.Google Scholar
[9]Dudley, R. M. (2002) Real Analysis and Probability, Cambridge University Press.CrossRefGoogle Scholar
[10]Fernholz, D. and Ramachandran, V. (2007) The diameter of sparse random graphs. Random Struct. Alg. 31 482–516.CrossRefGoogle Scholar
[11]Hammersley, J. M. and Welsh, D. J. A. (1965) First-passage percolation, sub-additive process, stochastic network and generalized renewal theory. In Bernoulli, 1713; Bayes, 1763; Laplace, 1813: Anniversary Volume, Springer.Google Scholar
[12]van der Hofstad, R. (2011) Random graphs and complex networks. In preparation. www.win.tue.nl/~rhofstad/NotesRGCN.pdf.Google Scholar
[13]van der Hofstad, R., Hooghiemstra, G. and Van Mieghem, P. (2001) First-passage percolation on the random graph. Probab. Engng Inform. Sci. 15 225–237.Google Scholar
[14]Howard, C. D. (2004) Models of first-passage percolation. In Probability on Discrete Structures, Springer, pp. 125–173.CrossRefGoogle Scholar
[15]Janson, S. (1999) One, two and three times log n/n for paths in a complete graph with random weights. Combin. Probab. Comput. 8 347–361.CrossRefGoogle Scholar
[16]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience.CrossRefGoogle Scholar
[17]Pittel, B. (1990) On tree census and the giant component in sparse random graphs. Random Struct. Alg. 1 311–342.CrossRefGoogle Scholar