Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:36:01.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Forbidden Subgraphs Generating Almost the Same Sets

Published online by Cambridge University Press:  11 July 2013

SHINYA FUJITA ,
MICHITAKA FURUYA  and
KENTA OZEKI
SHINYA FUJITA
Affiliation:
Department of Integrated Design Engineering, Maebashi Institute of Technology, 460-1 Kamisadori, Maebashi, Gunma 371-0816, Japan (e-mail: shinya.fujita.ph.d@gmail.com)
MICHITAKA FURUYA
Affiliation:
Department of Mathematical Information Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan (e-mail: michitaka.furuya@gmail.com)
KENTA OZEKI
Affiliation:
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan JST, ERATO, Kawarabayashi Large Graph Project, Japan (e-mail: ozeki@nii.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\mathcal{H}$ be a set of connected graphs. A graph G is said to be $\mathcal{H}$-free if G does not contain any element of $\mathcal{H}$ as an induced subgraph. Let 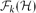$\mathcal{F}_{k}(\mathcal{H})$ be the set of k-connected $\mathcal{H}$-free graphs. When we study the relationship between forbidden subgraphs and a certain graph property, we often allow a finite exceptional set of graphs. But if the symmetric difference of 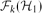$\mathcal{F}_{k}(\mathcal{H}_{1})$ and 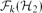$\mathcal{F}_{k}(\mathcal{H}_{2})$ is finite and we allow a finite number of exceptions, no graph property can distinguish them. Motivated by this observation, we study when we obtain a finite symmetric difference. In this paper, our main aim is the following. If 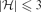$|\mathcal{H}|\leq 3$ and the symmetric difference of 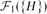$\mathcal{F}_{1}(\{H\})$ and 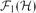$\mathcal{F}_{1}(\mathcal{H})$ is finite, then either 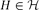$H\in \mathcal{H}$ or 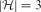$|\mathcal{H}|=3$ and H=C3. Furthermore, we prove that if the symmetric difference of 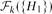$\mathcal{F}_{k}(\{H_{1}\})$ and 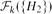$\mathcal{F}_{k}(\{H_{2}\})$ is finite, then H1=H2.

Keywords

05C75
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 5 , September 2013 , pp. 733 - 748
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aldred, R. E. L., Fujisawa, J. and Saito, A. (2010) Forbidden subgraphs and the existence of 2-factor. J. Graph Theory 64 250–266.Google Scholar
[2]Barrus, M. D., Kumbhat, M. and Hartke, S. G. (2008) Graph classes characterized both by forbidden subgraphs and degree sequences. J. Graph Theory 57 131–148.Google Scholar
[3]Bedrossian, P. (1991) Forbidden subgraphs and minimum degree conditions for Hamiltonicity. PhD thesis, University of Memphis.Google Scholar
[4]Broersma, H., Faudree, R. J., Huck, A., Trommel, H. and Veldman, H. J. (2002) Forbidden subgraphs that imply Hamiltonian-connectedness. J. Graph Theory 40 104–119.CrossRefGoogle Scholar
[5]Chartrand, G. and Lesniak, L. (2005) Graphs and Digraphs, fourth edition, Chapman & Hall/CRC.Google Scholar
[6]Cockayne, E. J., Ko, C. W. and Shepherd, F. B. (1985) Inequalities concerning dominating sets in graphs. Technical report DM-370-IR, Department of Mathematics, University of Victoria.Google Scholar
[7]Duffus, D., Gould, R. J. and Jacobson, M. S. (1981) Forbidden subgraphs and the Hamiltonian theme. In The Theory and Applications of Graphs (Chartrand, G.et al., eds), Wiley, pp. 297–316.Google Scholar
[8]Faudree, R. J. and Gould, R. J. (1997) Characterizing forbidden pairs for Hamiltonian properties. Discrete Math. 173 45–60.Google Scholar
[9]Faudree, R. J., Gould, R. J., Ryjáček, Z. and Schiermeyer, I. (1995) Forbidden subgraphs and pancyclicity. Congress Numer. 109 13–32.Google Scholar
[10]Fujisawa, J. and Saito, A. (2012) A pair of forbidden subgraphs and 2-factors. Combin. Probab. Comput. 21 149–158.Google Scholar
[11]Fujisawa, J., Fujita, S., Plummer, M. D., Saito, A. and Schiermeyer, I. (2011) A pair of forbidden subgraphs and perfect matchings in graphs of high connectivity. Combinatorica 31 703–723.Google Scholar
[12]Fujisawa, J., Ota, K., Ozeki, K. and Sueiro, G. (2011) Forbidden induced subgraphs for star-free graphs. Discrete Math. 311 2475–2484.Google Scholar
[13]Fujita, S., Kawarabayashi, K., Lucchesi, C. L., Ota, K., Plummer, M. and Saito, A. (2006) A pair of forbidden subgraphs and perfect matchings. J. Combin. Theory Ser. B 96 315–324.CrossRefGoogle Scholar
[14]Randerath, B. and Schiermeyer, I. (2004) Vertex colouring and forbidden subgraphs: A survey. Graphs Combin. 20 1–40.Google Scholar
[15]Xu, J. M. and Yang, C. (2006) Connectivity of Cartesian product graphs. Discrete Math. 306 159–165.Google Scholar