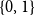1. Introduction
1.1 Background and motivation
Few subjects in combinatorics have had as profound an impact on other disciplines as combinatorial random matrix theory. Prominent applications include powerful error correcting codes called low-density parity check codes [Reference Richardson47], data compression [Reference Achlioptas and McSherry1, Reference Wainwright, Maneva and Martinian52] and hashing [Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19]. Needless to mention, random combinatorial matrices are of keen interest to statistical physicists, too [Reference Mézard40]. It therefore comes as no surprise that the subject has played a central role in probabilistic combinatorics since the early days [Reference Kolchin31–Reference Komlós34]. The current state of affairs is that the theory of dense random matrices is significantly more advanced than that of sparse ones with a bounded average number of non-zero entries per row or column [Reference Vu50, Reference Vu51]. This is in part because concentration techniques apply more easily in the dense case. Another reason is that the study of sparse random matrices is closely tied to the investigation of satisfiability thresholds of random constraint satisfaction problems, an area where many fundamental questions still await a satisfactory solution [Reference Achlioptas, Naor and Peres4].
Perhaps the most basic question to be asked about any random matrix model is whether the resulting matrix will likely have full rank. This paper contributes a succinct sufficient condition that covers a broad range of sparse random matrix models. As we will see, the condition is essentially necessary as well. The main result can be seen as a satisfiability threshold theorem as the full rank property is equivalent to a random linear system of equations possessing a solution w.h.p. This formulation generalises a number of prior results such as the satisfiability threshold theorem for the random
![]() $k$
-XORSAT problem, one of the most intensely studied random constraint satisfaction problems (e.g. [Reference Achlioptas and Molloy2, Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Dubois and Mandler21, Reference Ibrahimi, Kanoria, Kraning and Montanari28, Reference Pittel44]). In addition, the main theorem covers other important random matrix models, including those that low-density parity check codes rely on [Reference Richardson47].
$k$
-XORSAT problem, one of the most intensely studied random constraint satisfaction problems (e.g. [Reference Achlioptas and Molloy2, Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Dubois and Mandler21, Reference Ibrahimi, Kanoria, Kraning and Montanari28, Reference Pittel44]). In addition, the main theorem covers other important random matrix models, including those that low-density parity check codes rely on [Reference Richardson47].
The classical approach to tackling the full rank problem is the second moment method [Reference Achlioptas and Moore3, Reference Achlioptas, Naor and Peres4]. This technique was pioneered in the seminal work on the
![]() $k$
-XORSAT threshold of Dubois and Mandler [Reference Dubois and Mandler21]. Characteristic of this approach is the emergence of complicated analytic optimisation problems that encode entropy-probability trade-offs resulting from large deviations problems. Tackling these optimisation problems turns out to be rather challenging even in relatively simple special cases such as random
$k$
-XORSAT threshold of Dubois and Mandler [Reference Dubois and Mandler21]. Characteristic of this approach is the emergence of complicated analytic optimisation problems that encode entropy-probability trade-offs resulting from large deviations problems. Tackling these optimisation problems turns out to be rather challenging even in relatively simple special cases such as random
![]() $k$
-XORSAT, as witnessed by the intricate calculations that Pittel and Sorkin [Reference Pittel44] and Goerdt and Falke [Reference Goerdt and Falke23] had to go through. For the general model that we investigate here this proof technique thus appears futile.
$k$
-XORSAT, as witnessed by the intricate calculations that Pittel and Sorkin [Reference Pittel44] and Goerdt and Falke [Reference Goerdt and Falke23] had to go through. For the general model that we investigate here this proof technique thus appears futile.
We therefore pursue a totally different proof strategy, largely inspired by ideas from spin glass theory [Reference Mézard40, Reference Mézard and Ricci-Tersenghi41]. In statistical physics jargon, the second moment method constitutes an ‘annealed’ computation. This means that we effectively average over all random matrices, including atypical specimens apt to boost the average. By contrast, the present work relies on a ‘quenched’ strategy based on a coupling argument that implicitly discards such pathological events. In effect, we will show that a truncated moment calculation confined to certain benign ‘equitable’ solutions suffices to determine the satisfiability threshold. This part of the proof is an extension of prior work of (some of) the authors on the normalised rank and variations on the random
![]() $k$
-XORSAT problem [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. In addition, to actually compute the truncated second moment we need to determine the precise expected number of equitable solutions. To this end, we devise a new proof ingredient that combines local limit theorem techniques with algebraic ideas, particularly the combinatorial analysis of certain integer lattices. This technique can be seen as a generalisation of an argument of Huang [Reference Huang27] for the study of adjacency matrices of
$k$
-XORSAT problem [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. In addition, to actually compute the truncated second moment we need to determine the precise expected number of equitable solutions. To this end, we devise a new proof ingredient that combines local limit theorem techniques with algebraic ideas, particularly the combinatorial analysis of certain integer lattices. This technique can be seen as a generalisation of an argument of Huang [Reference Huang27] for the study of adjacency matrices of
![]() $d$
-regular random graphs.
$d$
-regular random graphs.
Let us proceed to present the main results of the paper. The first theorem deals with random matrices over finite fields. As an application we obtain a result on sparse
![]() $\{0,1\}$
-matrices over the rationals.
$\{0,1\}$
-matrices over the rationals.
1.2 Results
We work with the comprehensive random matrix model from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. Hence, let
![]() ${\boldsymbol{d}} \geq 0$
,
${\boldsymbol{d}} \geq 0$
,
![]() ${\boldsymbol{k}} \geq 3$
be independent integer-valued random variables with
${\boldsymbol{k}} \geq 3$
be independent integer-valued random variables with
![]() ${\mathbb{P}}({\boldsymbol{d}}=0)\lt 1$
and
${\mathbb{P}}({\boldsymbol{d}}=0)\lt 1$
and
![]() $\mathbb{E}[{\boldsymbol{d}}^{2+\eta }] + \mathbb{E}\left \lbrack{{\boldsymbol{k}}^{2+\eta }}\right \rbrack \lt \infty$
for an arbitrarily small
$\mathbb{E}[{\boldsymbol{d}}^{2+\eta }] + \mathbb{E}\left \lbrack{{\boldsymbol{k}}^{2+\eta }}\right \rbrack \lt \infty$
for an arbitrarily small
![]() $\eta \gt 0$
. Let
$\eta \gt 0$
. Let
![]() $({\boldsymbol{d}}_i,{\boldsymbol{k}}_i)_{i\geq 1}$
be independent copies of
$({\boldsymbol{d}}_i,{\boldsymbol{k}}_i)_{i\geq 1}$
be independent copies of
![]() $({\boldsymbol{d}}, {\boldsymbol{k}})$
and set
$({\boldsymbol{d}}, {\boldsymbol{k}})$
and set
![]() $d = \mathbb{E}[{\boldsymbol{d}}], k = \mathbb{E}[{\boldsymbol{k}}]$
. Moreover, let
$d = \mathbb{E}[{\boldsymbol{d}}], k = \mathbb{E}[{\boldsymbol{k}}]$
. Moreover, let
![]() $\mathfrak{d}$
and
$\mathfrak{d}$
and
![]() $\mathfrak{k}$
be the greatest common divisors of the support of
$\mathfrak{k}$
be the greatest common divisors of the support of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
, respectively. Further, let
${\boldsymbol{k}}$
, respectively. Further, let
![]() $n\gt 0$
be an integer divisible by
$n\gt 0$
be an integer divisible by
![]() $\mathfrak{k}$
and let
$\mathfrak{k}$
and let
![]() ${\boldsymbol{m}}$
be a Poisson variable with mean
${\boldsymbol{m}}$
be a Poisson variable with mean
![]() $dn/k$
, independent of
$dn/k$
, independent of
![]() $({\boldsymbol{d}}_i,{\boldsymbol{k}}_i)_{i\geq 1}$
. Routine arguments reveal that the event
$({\boldsymbol{d}}_i,{\boldsymbol{k}}_i)_{i\geq 1}$
. Routine arguments reveal that the event
 \begin{align} \sum _{i=1}^n {\boldsymbol{d}}_i = \sum _{j=1}^{{\boldsymbol{m}}} {\boldsymbol{k}}_j \end{align}
\begin{align} \sum _{i=1}^n {\boldsymbol{d}}_i = \sum _{j=1}^{{\boldsymbol{m}}} {\boldsymbol{k}}_j \end{align}
occurs with probability
![]() $\Omega (n^{-1/2})$
for such
$\Omega (n^{-1/2})$
for such
![]() $n$
[Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proposition 1.10]. Given (1.1), we then define the simple random bipartite graph
$n$
[Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proposition 1.10]. Given (1.1), we then define the simple random bipartite graph
![]() ${\mathbb{G}}={\mathbb{G}}_n({\boldsymbol{d}},{\boldsymbol{k}})$
on a set
${\mathbb{G}}={\mathbb{G}}_n({\boldsymbol{d}},{\boldsymbol{k}})$
on a set
![]() $\left \{{a_1 \ldots, a_{{\boldsymbol{m}}}}\right \}$
of check nodes and a set
$\left \{{a_1 \ldots, a_{{\boldsymbol{m}}}}\right \}$
of check nodes and a set
![]() $\left \{{x_1,\ldots,x_n}\right \}$
of variable nodes as a uniformly random simple graph such that the degree of
$\left \{{x_1,\ldots,x_n}\right \}$
of variable nodes as a uniformly random simple graph such that the degree of
![]() $a_i$
equals
$a_i$
equals
![]() ${\boldsymbol{k}}_i$
and the degree of
${\boldsymbol{k}}_i$
and the degree of
![]() $x_j$
equals
$x_j$
equals
![]() ${\boldsymbol{d}}_j$
, for all
${\boldsymbol{d}}_j$
, for all
![]() $i, j$
. The existence of such a graph is proven in [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proposition 1.10]. Following coding theory jargon, we refer to
$i, j$
. The existence of such a graph is proven in [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proposition 1.10]. Following coding theory jargon, we refer to
![]() $\mathbb{G}$
as the Tanner graph. The edges of
$\mathbb{G}$
as the Tanner graph. The edges of
![]() $\mathbb{G}$
are going to mark the positions of the non-zero entries of the random matrix. The entries themselves will depend on whether we deal with a finite field or the rationals.
$\mathbb{G}$
are going to mark the positions of the non-zero entries of the random matrix. The entries themselves will depend on whether we deal with a finite field or the rationals.
1.2.1 Finite fields
Suppose that
![]() $q \geq 2$
is a prime power, let
$q \geq 2$
is a prime power, let
![]() $\mathbb{F}_q$
signify the field with
$\mathbb{F}_q$
signify the field with
![]() $q$
elements and let
$q$
elements and let
![]() $\boldsymbol{\chi }$
be a random variable that takes values in the set
$\boldsymbol{\chi }$
be a random variable that takes values in the set
![]() $\mathbb{F}_q^\ast = \mathbb{F}_q \setminus \{0\}$
of units of
$\mathbb{F}_q^\ast = \mathbb{F}_q \setminus \{0\}$
of units of
![]() $\mathbb{F}_q$
. Moreover, let
$\mathbb{F}_q$
. Moreover, let
![]() $(\boldsymbol{\chi }_{i,j})_{i,j\geq 1}$
be copies of
$(\boldsymbol{\chi }_{i,j})_{i,j\geq 1}$
be copies of
![]() $\boldsymbol{\chi }$
, mutually independent and independent of the
$\boldsymbol{\chi }$
, mutually independent and independent of the
![]() ${\boldsymbol{d}}_i,{\boldsymbol{k}}_i$
,
${\boldsymbol{d}}_i,{\boldsymbol{k}}_i$
,
![]() ${\boldsymbol{m}}$
and
${\boldsymbol{m}}$
and
![]() $\mathbb{G}$
. Finally, let
$\mathbb{G}$
. Finally, let
![]() $\mathbb{A}=\mathbb{A}_n({\boldsymbol{d}},{\boldsymbol{k}},\boldsymbol{\chi })$
be the
$\mathbb{A}=\mathbb{A}_n({\boldsymbol{d}},{\boldsymbol{k}},\boldsymbol{\chi })$
be the
![]() ${\boldsymbol{m}} \times n$
-matrix with entries
${\boldsymbol{m}} \times n$
-matrix with entries
Hence, the
![]() $i$
-th row of
$i$
-th row of
![]() $\mathbb{A}$
contains
$\mathbb{A}$
contains
![]() ${\boldsymbol{k}}_i$
non-zero entries and the
${\boldsymbol{k}}_i$
non-zero entries and the
![]() $j$
-th column contains
$j$
-th column contains
![]() ${\boldsymbol{d}}_j$
non-zero entries.
${\boldsymbol{d}}_j$
non-zero entries.
The following theorem provides a sufficient condition for
![]() $\mathbb{A}$
having full row rank. The condition comes in terms of the probability generating functions
$\mathbb{A}$
having full row rank. The condition comes in terms of the probability generating functions
![]() $D(x)$
and
$D(x)$
and
![]() $K(x)$
of
$K(x)$
of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
. Since
${\boldsymbol{k}}$
. Since
![]() $\mathbb{E}[{\boldsymbol{d}}^2]+\mathbb{E}[{\boldsymbol{k}}^2]\lt \infty$
, we may define
$\mathbb{E}[{\boldsymbol{d}}^2]+\mathbb{E}[{\boldsymbol{k}}^2]\lt \infty$
, we may define
Theorem 1.1.
Let
![]() $\textbf{d} \geq 0, {\boldsymbol{k}} \geq 3$
and
$\textbf{d} \geq 0, {\boldsymbol{k}} \geq 3$
and
![]() $q$
be a fixed prime power such that
$q$
be a fixed prime power such that
![]() $\mathfrak{d} = \text{gcd}(\text{supp}({\boldsymbol{d}}))$
and
$\mathfrak{d} = \text{gcd}(\text{supp}({\boldsymbol{d}}))$
and
![]() $q$
are coprime. If
$q$
are coprime. If
then
![]() $\mathbb{A}$
has full row rank over
$\mathbb{A}$
has full row rank over
![]() $\mathbb{F}_q$
w.h.p.
$\mathbb{F}_q$
w.h.p.
Observe that the function
![]() $\Phi$
does not depend on
$\Phi$
does not depend on
![]() $q$
. Hence, neither does (1.3).
$q$
. Hence, neither does (1.3).
The sufficient condition (1.3) is generally necessary, too. Indeed, ref. [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Theorem 1.1] determines the likely value of the normalised rank of
![]() $\mathbb{A}$
:
$\mathbb{A}$
:
Since
![]() ${\boldsymbol{k}}\geq 3$
, definition (1.2) ensures that
${\boldsymbol{k}}\geq 3$
, definition (1.2) ensures that
![]() $\Phi (0)=1-d/k$
and thus
$\Phi (0)=1-d/k$
and thus
![]() $n\Phi (0)\sim n-{\boldsymbol{m}}$
w.h.p. Hence, (1.4) implies that
$n\Phi (0)\sim n-{\boldsymbol{m}}$
w.h.p. Hence, (1.4) implies that
![]() ${\text{rk}}(\mathbb{A})\leq {\boldsymbol{m}}-\Omega (n)$
w.h.p. unless
${\text{rk}}(\mathbb{A})\leq {\boldsymbol{m}}-\Omega (n)$
w.h.p. unless
![]() $\Phi (z)$
attains its maximum at
$\Phi (z)$
attains its maximum at
![]() $z=0$
. In other words,
$z=0$
. In other words,
![]() $\mathbb{A}$
has full row rank only if
$\mathbb{A}$
has full row rank only if
![]() $\Phi (z)\leq \Phi (0)$
for all
$\Phi (z)\leq \Phi (0)$
for all
![]() $0\lt z\leq 1$
. Indeed, in Section 1.3 we will discover examples that require a strict inequality as in (1.3). The condition that
$0\lt z\leq 1$
. Indeed, in Section 1.3 we will discover examples that require a strict inequality as in (1.3). The condition that
![]() $q$
and
$q$
and
![]() $\mathfrak{d}$
be coprime is generally necessary as well, as we will see in Example 1.7 below.
$\mathfrak{d}$
be coprime is generally necessary as well, as we will see in Example 1.7 below.
Let us emphasise that (1.4) does not guarantee that
![]() $\mathbb{A}$
has full row rank w.h.p. even if (1.3) is satisfied. Rather due to the normalisation of the l.h.s. (1.4) only implies the much weaker statement
$\mathbb{A}$
has full row rank w.h.p. even if (1.3) is satisfied. Rather due to the normalisation of the l.h.s. (1.4) only implies the much weaker statement
![]() ${\text{rk}}(\mathbb{A})={\boldsymbol{m}}-o(n)$
w.h.p. Hence, in the case that (1.3) is satisfied, Theorem 1.1 improves over the asymptotic estimate (1.4) rather substantially. Unsurprisingly, this stronger result also requires a more delicate proof strategy.
${\text{rk}}(\mathbb{A})={\boldsymbol{m}}-o(n)$
w.h.p. Hence, in the case that (1.3) is satisfied, Theorem 1.1 improves over the asymptotic estimate (1.4) rather substantially. Unsurprisingly, this stronger result also requires a more delicate proof strategy.
We finally remark that condition (1.3) in combination with (1.4) enforces that
![]() $d \leq k$
. Moreover, if
$d \leq k$
. Moreover, if
![]() $d=k$
, then
$d=k$
, then
![]() $\Phi (0) = 0 \leq D(0) = \Phi (1)$
, such that condition (1.3) also cannot be satisfied for such
$\Phi (0) = 0 \leq D(0) = \Phi (1)$
, such that condition (1.3) also cannot be satisfied for such
![]() $d,k$
. Thus,
$d,k$
. Thus,
![]() $d \lt k$
for all matrices to which Theorem 1.1 applies, and the subject of Theorem 1.1 is the rank of rectangular matrices with asymptotically more columns than rows. For sparse and square Bernoulli matrices, Glasgow, Kwan, Sah and Sawhney [Reference Glasgow, Kwan, Sah and Sawhney24] recently provided precise combinatorial descriptions of the exact real rank. The method of [Reference Glasgow, Kwan, Sah and Sawhney24] applies to both symmetric and asymmetric Bernoulli matrices and relates the real rank to the Karp-Sipser core of the associated graph models. Theorem 1.1 also does not make a quantitative statement about the rate of convergence. While such a quantification could in principle be obtained from our proof, we do not expect it to be very close to optimal and have therefore not pursued this.
$d \lt k$
for all matrices to which Theorem 1.1 applies, and the subject of Theorem 1.1 is the rank of rectangular matrices with asymptotically more columns than rows. For sparse and square Bernoulli matrices, Glasgow, Kwan, Sah and Sawhney [Reference Glasgow, Kwan, Sah and Sawhney24] recently provided precise combinatorial descriptions of the exact real rank. The method of [Reference Glasgow, Kwan, Sah and Sawhney24] applies to both symmetric and asymmetric Bernoulli matrices and relates the real rank to the Karp-Sipser core of the associated graph models. Theorem 1.1 also does not make a quantitative statement about the rate of convergence. While such a quantification could in principle be obtained from our proof, we do not expect it to be very close to optimal and have therefore not pursued this.
1.2.2 Zero-one matrices over the rationals
Apart from matrices over finite fields, the rational rank of sparse random
![]() $\{0,1\}$
-matrices has received a great deal of attention [Reference Vu50, Reference Vu51]. The random graph
$\{0,1\}$
-matrices has received a great deal of attention [Reference Vu50, Reference Vu51]. The random graph
![]() $\mathbb{G}$
naturally induces a
$\mathbb{G}$
naturally induces a
![]() $\{0,1\}$
-matrix, namely the
$\{0,1\}$
-matrix, namely the
![]() ${\boldsymbol{m}}\times n$
-biadjacency matrix
${\boldsymbol{m}}\times n$
-biadjacency matrix
![]() $\mathbb{B}=\mathbb{B}({\mathbb{G}})$
. Explicitly,
$\mathbb{B}=\mathbb{B}({\mathbb{G}})$
. Explicitly,
![]() $\mathbb{B}_{ij}={\mathbb{1}}\{a_ix_j\in E({\mathbb{G}})\}$
. As an application of Theorem 1.1 we obtain the following result.
$\mathbb{B}_{ij}={\mathbb{1}}\{a_ix_j\in E({\mathbb{G}})\}$
. As an application of Theorem 1.1 we obtain the following result.
Corollary 1.2.
If (1.3) is satisfied then the random matrix
![]() $\mathbb{B}$
has full row rank over
$\mathbb{B}$
has full row rank over
![]() $\mathbb{Q}$
w.h.p.
$\mathbb{Q}$
w.h.p.
Since (1.4) holds for random matrices over the rationals as well, Corollary 1.2 is optimal to the extent that
![]() $\mathbb{B}$
fails to have full row rank w.h.p. if
$\mathbb{B}$
fails to have full row rank w.h.p. if
![]() $\max _{x\in [0,1]}\Phi (x)\gt \Phi (0)$
. Moreover, in Example 1.4 we will see that
$\max _{x\in [0,1]}\Phi (x)\gt \Phi (0)$
. Moreover, in Example 1.4 we will see that
![]() $\mathbb{B}$
does not generally have full rank w.h.p. unless
$\mathbb{B}$
does not generally have full rank w.h.p. unless
![]() $x=0$
is the unique maximiser of
$x=0$
is the unique maximiser of
![]() $\Phi$
.
$\Phi$
.
1.2.3 Fixed-degree sequences
In Section 2.3, we consider a more general model for
![]() $\mathbb{A}$
, where the sequences
$\mathbb{A}$
, where the sequences
![]() $(d_i)_{i \geq 1}$
and
$(d_i)_{i \geq 1}$
and
![]() $(k_j)_{j \geq 1}$
are specified instead of being obtained by taking i.i.d. copies of
$(k_j)_{j \geq 1}$
are specified instead of being obtained by taking i.i.d. copies of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
. Under analogous conditions like (1.3) together with some additional ‘smoothness’ conditions for
${\boldsymbol{k}}$
. Under analogous conditions like (1.3) together with some additional ‘smoothness’ conditions for
![]() $d_1,\ldots,d_n$
and
$d_1,\ldots,d_n$
and
![]() $k_1,\ldots,k_m$
, we also show that the matrix
$k_1,\ldots,k_m$
, we also show that the matrix
![]() $\underline{\mathbb{A}}$
corresponding to the fixed-degree setting has full row rank (see Proposition 2.1).
$\underline{\mathbb{A}}$
corresponding to the fixed-degree setting has full row rank (see Proposition 2.1).
1.3 Examples
To illustrate the power of Theorem 1.1 and Corollary 1.2 we consider a few instructive special cases of distributions
![]() ${\boldsymbol{d}},{\boldsymbol{k}},\boldsymbol{\chi }$
.
${\boldsymbol{d}},{\boldsymbol{k}},\boldsymbol{\chi }$
.
Example 1.3 (random
![]() $k$
-XORSAT). In random
$k$
-XORSAT). In random
![]() $k$
-XORSAT we are handed a number of independent random constraints
$k$
-XORSAT we are handed a number of independent random constraints
![]() $c_i$
of the type
$c_i$
of the type
where each
![]() $y_{ij}$
is either one of
$y_{ij}$
is either one of
![]() $n$
available Boolean variables
$n$
available Boolean variables
![]() $x_1,\ldots,x_n$
or a negation
$x_1,\ldots,x_n$
or a negation
![]() $\neg x_1,\ldots,\neg x_n$
. The obvious question is to determine the satisfiability threshold, that is, the maximum number of random constraints that can be satisfied simultaneously w.h.p.
$\neg x_1,\ldots,\neg x_n$
. The obvious question is to determine the satisfiability threshold, that is, the maximum number of random constraints that can be satisfied simultaneously w.h.p.
Because Boolean XOR boils down to addition over
![]() $\mathbb{F}_2$
, this problem can be rephrased as the full rank problem for the random matrix
$\mathbb{F}_2$
, this problem can be rephrased as the full rank problem for the random matrix
![]() $\mathbb{A}$
with
$\mathbb{A}$
with
![]() $q=2$
,
$q=2$
,
![]() ${\boldsymbol{k}}=k$
fixed to a deterministic value and
${\boldsymbol{k}}=k$
fixed to a deterministic value and
![]() ${\boldsymbol{d}}\sim \text{Po}(d)$
for a parameter
${\boldsymbol{d}}\sim \text{Po}(d)$
for a parameter
![]() $d\gt 0$
. To elaborate, because the constraints
$d\gt 0$
. To elaborate, because the constraints
![]() $c_i$
are drawn uniformly and independently, we can think of each as tossing
$c_i$
are drawn uniformly and independently, we can think of each as tossing
![]() $k$
balls randomly into
$k$
balls randomly into
![]() $n$
bins that represent
$n$
bins that represent
![]() $x_1,\ldots,x_n$
. If there are
$x_1,\ldots,x_n$
. If there are
![]() ${\boldsymbol{m}}\sim \text{Po}(dn/k)$
constraints
${\boldsymbol{m}}\sim \text{Po}(dn/k)$
constraints
![]() $c_i$
, the joint distribution of the variable degrees coincides with the distribution of
$c_i$
, the joint distribution of the variable degrees coincides with the distribution of
![]() $({\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n)$
subject to the condition (1.1). Furthermore, the random negation patterns of the constraints (1.5) amount to choosing a random right-hand side vector
$({\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n)$
subject to the condition (1.1). Furthermore, the random negation patterns of the constraints (1.5) amount to choosing a random right-hand side vector
![]() ${\boldsymbol{y}}$
for which we are to solve
${\boldsymbol{y}}$
for which we are to solve
![]() $\mathbb{A} x={\boldsymbol{y}}$
.
$\mathbb{A} x={\boldsymbol{y}}$
.
Since the generating functions of
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
work out to be
${\boldsymbol{d}},{\boldsymbol{k}}$
work out to be
![]() $D(z)=\exp\!(d(z-1))$
and
$D(z)=\exp\!(d(z-1))$
and
![]() $K(z)=z^k$
, we obtain
$K(z)=z^k$
, we obtain
Thus, Theorem 1.1 implies that for a given
![]() $k\geq 3$
the threshold of
$k\geq 3$
the threshold of
![]() $d$
up to which random
$d$
up to which random
![]() $k$
-XORSAT is satisfiable w.h.p. equals the largest
$k$
-XORSAT is satisfiable w.h.p. equals the largest
![]() $d$
such that
$d$
such that
A few lines of calculus verify that (1.6) matches the formulas for the
![]() $k$
-XORSAT threshold derived by combinatorial methods tailored to this specific case [Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Dubois and Mandler21, Reference Mézard and Ricci-Tersenghi41, Reference Pittel44]. Theorem 1.1 also encompasses the generalisations to other finite fields
$k$
-XORSAT threshold derived by combinatorial methods tailored to this specific case [Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Dubois and Mandler21, Reference Mézard and Ricci-Tersenghi41, Reference Pittel44]. Theorem 1.1 also encompasses the generalisations to other finite fields
![]() $\mathbb{F}_q$
from [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Goerdt and Falke23]. (For
$\mathbb{F}_q$
from [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Goerdt and Falke23]. (For
![]() $d=6.5$
and
$d=6.5$
and
![]() $k=7$
see the left of Fig. 1.)
$k=7$
see the left of Fig. 1.)
Example 1.4 (identical distributions). An interesting scenario arises when
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
are identically distributed. For example, suppose that
${\boldsymbol{d}},{\boldsymbol{k}}$
are identically distributed. For example, suppose that
![]() ${\mathbb{P}}[{\boldsymbol{d}}=3]={\mathbb{P}}[{\boldsymbol{d}}=4]={\mathbb{P}}[{\boldsymbol{k}}=3]={\mathbb{P}}[{\boldsymbol{k}}=4]=1/2$
. Thus,
${\mathbb{P}}[{\boldsymbol{d}}=3]={\mathbb{P}}[{\boldsymbol{d}}=4]={\mathbb{P}}[{\boldsymbol{k}}=3]={\mathbb{P}}[{\boldsymbol{k}}=4]=1/2$
. Thus,
![]() $D(z)=K(z)=(z^3+z^4)/2$
and
$D(z)=K(z)=(z^3+z^4)/2$
and
This function attains two identical maxima, namely
![]() $\Phi (0)=\Phi (1)=0$
(See the right of Fig. 1). Since the degrees
$\Phi (0)=\Phi (1)=0$
(See the right of Fig. 1). Since the degrees
![]() ${\boldsymbol{k}}_i,{\boldsymbol{d}}_i$
are chosen independently subject only to (1.1), the probability that
${\boldsymbol{k}}_i,{\boldsymbol{d}}_i$
are chosen independently subject only to (1.1), the probability that
![]() $\mathbb{A}$
has more rows than columns works out to be
$\mathbb{A}$
has more rows than columns works out to be
![]() $1/2+o(1)$
. As a consequence,
$1/2+o(1)$
. As a consequence,
![]() $\mathbb{A}$
cannot have full row rank w.h.p. This example shows that the condition that
$\mathbb{A}$
cannot have full row rank w.h.p. This example shows that the condition that
![]() $0$
be the unique maximiser of
$0$
be the unique maximiser of
![]() $\Phi (x)$
is generally necessary to ensure that
$\Phi (x)$
is generally necessary to ensure that
![]() $\mathbb{A}$
has full row rank. The same applies to the rational rank of
$\mathbb{A}$
has full row rank. The same applies to the rational rank of
![]() $\mathbb{B}$
.
$\mathbb{B}$
.
Example 1.5 (fixed
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
). Suppose that both
${\boldsymbol{d}},{\boldsymbol{k}}$
). Suppose that both
![]() ${\boldsymbol{d}}=d,{\boldsymbol{k}}=k\geq 3$
are constants rather than genuinely random. Then
${\boldsymbol{d}}=d,{\boldsymbol{k}}=k\geq 3$
are constants rather than genuinely random. Then
Clearly,
![]() $\mathbb{A}$
cannot have full row rank unless
$\mathbb{A}$
cannot have full row rank unless
![]() $d\leq k$
, while Theorem 1.1 implies that
$d\leq k$
, while Theorem 1.1 implies that
![]() $\mathbb{A}$
has full row rank w.h.p. if
$\mathbb{A}$
has full row rank w.h.p. if
![]() $d\lt k$
(See the left of Fig. 2). This result was previously established via the second moment method [Reference Miller and Cohen42]. But in the critical case
$d\lt k$
(See the left of Fig. 2). This result was previously established via the second moment method [Reference Miller and Cohen42]. But in the critical case
![]() $d=k$
the function
$d=k$
the function
![]() $\Phi (z)$
attains its identical maxima at
$\Phi (z)$
attains its identical maxima at
![]() $z=0$
and
$z=0$
and
![]() $z=1$
. Specifically,
$z=1$
. Specifically,
![]() $0=\Phi (0)=\Phi (1)\gt \Phi (z)$
for all
$0=\Phi (0)=\Phi (1)\gt \Phi (z)$
for all
![]() $0\lt z\lt 1$
. Hence, Theorem 1.1 does not cover this special case. Nonetheless, Huang [Reference Huang27] proved that the random
$0\lt z\lt 1$
. Hence, Theorem 1.1 does not cover this special case. Nonetheless, Huang [Reference Huang27] proved that the random
![]() $\{0,1\}$
-matrix
$\{0,1\}$
-matrix
![]() $\mathbb{B}$
has full rational rank w.h.p. The proof is based on a delicate moment computation in combination with a precise local expansion around the equitable solutions.
$\mathbb{B}$
has full rational rank w.h.p. The proof is based on a delicate moment computation in combination with a precise local expansion around the equitable solutions.
Example 1.6 (power laws). Let
![]() ${\mathbb{P}}({\boldsymbol{d}} = \ell ) \propto \ell ^{-\alpha }$
for some
${\mathbb{P}}({\boldsymbol{d}} = \ell ) \propto \ell ^{-\alpha }$
for some
![]() $\alpha \gt 3$
and
$\alpha \gt 3$
and
![]() $ {\boldsymbol{k}} = k \geq 3$
. Thus,
$ {\boldsymbol{k}} = k \geq 3$
. Thus,
 \begin{align*} D(z) &= \frac 1{\zeta (\alpha )}\sum _{\ell = 1}^{\infty }\frac{z^\ell }{\ell ^{\alpha }},\quad K(z) = z^k,\\[5pt] \Phi (z) &= D\left ({1-z^{k-1}}\right ) - \frac{\zeta ^{-1}(\alpha )\zeta (\alpha -1)}{k} \left ({1 - k z^{k-1}+ (k-1)z^{k} }\right ). \end{align*}
\begin{align*} D(z) &= \frac 1{\zeta (\alpha )}\sum _{\ell = 1}^{\infty }\frac{z^\ell }{\ell ^{\alpha }},\quad K(z) = z^k,\\[5pt] \Phi (z) &= D\left ({1-z^{k-1}}\right ) - \frac{\zeta ^{-1}(\alpha )\zeta (\alpha -1)}{k} \left ({1 - k z^{k-1}+ (k-1)z^{k} }\right ). \end{align*}
Since
the function
![]() $\Phi (z)$
is strictly decreasing on
$\Phi (z)$
is strictly decreasing on
![]() $(0,1)$
. Therefore, (1.3) is satisfied (For
$(0,1)$
. Therefore, (1.3) is satisfied (For
![]() $ \alpha = 3.5 $
and
$ \alpha = 3.5 $
and
![]() $k = 3$
see the right of Fig. 2).
$k = 3$
see the right of Fig. 2).
Example 1.7 (zero row sums). Theorem 1.1 requires the assumption that
![]() $q$
and the g.c.d.
$q$
and the g.c.d.
![]() $\mathfrak{d}$
of the support of
$\mathfrak{d}$
of the support of
![]() ${\boldsymbol{d}}$
be coprime. This assumption is indeed necessary. To see this, consider the case that
${\boldsymbol{d}}$
be coprime. This assumption is indeed necessary. To see this, consider the case that
![]() $q=2$
,
$q=2$
,
![]() $\boldsymbol{\chi }=1$
,
$\boldsymbol{\chi }=1$
,
![]() ${\boldsymbol{d}}=4$
and
${\boldsymbol{d}}=4$
and
![]() ${\boldsymbol{k}}=8$
deterministically. Then the rows of
${\boldsymbol{k}}=8$
deterministically. Then the rows of
![]() $\mathbb{A}$
always sum to zero. Hence,
$\mathbb{A}$
always sum to zero. Hence,
![]() $\mathbb{A}$
cannot have full row rank.
$\mathbb{A}$
cannot have full row rank.
2. Overview
In contrast to much of the prior work on the rank problem, random
![]() $k$
-XORSAT and random constraint satisfaction problems generally, the proofs of the main results do not rely on an ‘annealed’ second moment computation. Such arguments appear to be far too susceptible to large deviation effects to extend to as general a random matrix model as we deal with here. Instead, we proceed by way of a ‘quenched’ argument that enables us to discard pathological events. As a result, it suffices to carry out the moment calculation in the particularly benign case of ‘equitable’ solutions.
$k$
-XORSAT and random constraint satisfaction problems generally, the proofs of the main results do not rely on an ‘annealed’ second moment computation. Such arguments appear to be far too susceptible to large deviation effects to extend to as general a random matrix model as we deal with here. Instead, we proceed by way of a ‘quenched’ argument that enables us to discard pathological events. As a result, it suffices to carry out the moment calculation in the particularly benign case of ‘equitable’ solutions.
This proof strategy draws on but substantially generalises tools that were developed towards the approximate rank formula (1.4) and variations on random
![]() $k$
-XORSAT [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. In addition, to actually prove that
$k$
-XORSAT [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. In addition, to actually prove that
![]() $\mathbb{A}$
has full rank with high probability we will need to carry out a meticulous, asymptotically exact calculation of the expected number of equitable solutions. A key element of this analysis will be a delicate analysis of the lattices generated by certain integer vectors that encode conceivable equitable solutions. This part of the proof, which generalises a part of Huang’s argument for the adjacency matrices of random
$\mathbb{A}$
has full rank with high probability we will need to carry out a meticulous, asymptotically exact calculation of the expected number of equitable solutions. A key element of this analysis will be a delicate analysis of the lattices generated by certain integer vectors that encode conceivable equitable solutions. This part of the proof, which generalises a part of Huang’s argument for the adjacency matrices of random
![]() $d$
-regular graphs [Reference Huang27], combines local limit techniques with a whiff of linear algebra.
$d$
-regular graphs [Reference Huang27], combines local limit techniques with a whiff of linear algebra.
To describe the proof strategy in detail let us first explore the ‘annealed’ path, discover its pitfalls and then apply the lessons learned to develop a workable ‘quenched’ strategy. The bulk of the proof deals with the random matrix model from Section 1.2.1 over the finite field
![]() $\mathbb{F}_q$
; the rational case from Corollary 1.2 comes out as an easy consequence.
$\mathbb{F}_q$
; the rational case from Corollary 1.2 comes out as an easy consequence.
In order to reduce fluctuations we are going to condition on the
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathfrak{A}$
generated by
$\mathfrak{A}$
generated by
![]() ${\boldsymbol{m}},({\boldsymbol{k}}_i)_{i\geq 1},({\boldsymbol{d}}_i)_{i\geq 1}$
and by the numbers
${\boldsymbol{m}},({\boldsymbol{k}}_i)_{i\geq 1},({\boldsymbol{d}}_i)_{i\geq 1}$
and by the numbers
![]() ${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of checks of degree
${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of checks of degree
![]() $\ell \geq 3$
with coefficients
$\ell \geq 3$
with coefficients
![]() $\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
. We write
$\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
. We write
![]() ${\mathbb{P}}_{\mathfrak{A}}={\mathbb{P}}\left \lbrack{\,\cdot \,\mid \mathfrak{A}}\right \rbrack$
and
${\mathbb{P}}_{\mathfrak{A}}={\mathbb{P}}\left \lbrack{\,\cdot \,\mid \mathfrak{A}}\right \rbrack$
and
![]() $\mathbb{E}_{\mathfrak{A}}=\mathbb{E}\left \lbrack{\,\cdot \,\mid \mathfrak{A}}\right \rbrack$
for brevity.
$\mathbb{E}_{\mathfrak{A}}=\mathbb{E}\left \lbrack{\,\cdot \,\mid \mathfrak{A}}\right \rbrack$
for brevity.
2.1 Moments and deviations
We already alluded to how the full rank problem for the random matrix
![]() $\mathbb{A}$
over
$\mathbb{A}$
over
![]() $\mathbb{F}_q$
can be viewed as a random constraint satisfaction problem. Indeed, suppose we draw a right-hand side vector
$\mathbb{F}_q$
can be viewed as a random constraint satisfaction problem. Indeed, suppose we draw a right-hand side vector
![]() ${\boldsymbol{y}}\in \mathbb{F}_q^{{\boldsymbol{m}}}$
independently of
${\boldsymbol{y}}\in \mathbb{F}_q^{{\boldsymbol{m}}}$
independently of
![]() $\mathbb{A}$
. Then
$\mathbb{A}$
. Then
![]() $\mathbb{A}$
has full row rank w.h.p. iff the random linear system
$\mathbb{A}$
has full row rank w.h.p. iff the random linear system
![]() $\mathbb{A} x={\boldsymbol{y}}$
admits a solution w.h.p. For if
$\mathbb{A} x={\boldsymbol{y}}$
admits a solution w.h.p. For if
![]() ${\text{rk}}\mathbb{A}\lt {\boldsymbol{m}}$
, then the image
${\text{rk}}\mathbb{A}\lt {\boldsymbol{m}}$
, then the image
![]() $\mathbb{A} \mathbb{F}_q^n$
is a proper subspace of
$\mathbb{A} \mathbb{F}_q^n$
is a proper subspace of
![]() $\mathbb{F}_q^{{\boldsymbol{m}}}$
and thus the random linear system
$\mathbb{F}_q^{{\boldsymbol{m}}}$
and thus the random linear system
![]() $\mathbb{A} x={\boldsymbol{y}}$
has a solution with probability at most
$\mathbb{A} x={\boldsymbol{y}}$
has a solution with probability at most
![]() $1/q$
. Naturally, the random linear system is nothing but a random constraint satisfaction problem with
$1/q$
. Naturally, the random linear system is nothing but a random constraint satisfaction problem with
![]() ${\boldsymbol{m}}$
constraints and
${\boldsymbol{m}}$
constraints and
![]() $n$
variables.
$n$
variables.
Over the past two decades the second moment method has emerged as the default approach to pinpointing satisfiability thresholds of random constraint satisfaction problems [Reference Achlioptas and Moore3, Reference Achlioptas, Naor and Peres4]. Indeed, one of the first success stories was the random
![]() $3$
-XORSAT problem, which boils down directly to a full rank problem over
$3$
-XORSAT problem, which boils down directly to a full rank problem over
![]() $\mathbb{F}_2$
[Reference Dubois and Mandler21]. In fact, as we saw in Example 1.3, to mimic
$\mathbb{F}_2$
[Reference Dubois and Mandler21]. In fact, as we saw in Example 1.3, to mimic
![]() $3$
-XORSAT we just set
$3$
-XORSAT we just set
![]() $q=2$
,
$q=2$
,
![]() ${\boldsymbol{d}}=\text{Po}(d)$
for some
${\boldsymbol{d}}=\text{Po}(d)$
for some
![]() $d\gt 0$
and
$d\gt 0$
and
![]() ${\boldsymbol{k}}=3$
deterministically. In addition, draw
${\boldsymbol{k}}=3$
deterministically. In addition, draw
![]() ${\boldsymbol{y}}\in \mathbb{F}_2^{{\boldsymbol{m}}}$
uniformly and independently of everything else.
${\boldsymbol{y}}\in \mathbb{F}_2^{{\boldsymbol{m}}}$
uniformly and independently of everything else.
We try the second moment method on the number
![]() ${\boldsymbol{Z}}={\boldsymbol{Z}}(\mathbb{A},{\boldsymbol{y}})$
of solutions to
${\boldsymbol{Z}}={\boldsymbol{Z}}(\mathbb{A},{\boldsymbol{y}})$
of solutions to
![]() $\mathbb{A} x={\boldsymbol{y}}$
given
$\mathbb{A} x={\boldsymbol{y}}$
given
![]() $\mathfrak{A}$
. Since
$\mathfrak{A}$
. Since
![]() ${\boldsymbol{y}}$
is independent of
${\boldsymbol{y}}$
is independent of
![]() $\mathbb{A}$
, for any fixed vector
$\mathbb{A}$
, for any fixed vector
![]() $x\in \mathbb{F}_2^n$
the event
$x\in \mathbb{F}_2^n$
the event
![]() $\mathbb{A} x={\boldsymbol{y}}$
has probability
$\mathbb{A} x={\boldsymbol{y}}$
has probability
![]() $2^{-{\boldsymbol{m}}}$
. Consequently,
$2^{-{\boldsymbol{m}}}$
. Consequently,
Hence, (2.1) recovers the obvious condition that we cannot have more rows than columns. Since
![]() ${\boldsymbol{m}}\sim \text{Po}(dn/3)$
, (2.1) boils down to
${\boldsymbol{m}}\sim \text{Po}(dn/3)$
, (2.1) boils down to
![]() $d\lt 3$
.
$d\lt 3$
.
The second moment method now rests on the hope that we may be able to show that
![]() $\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]\sim \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]^2$
. Then Chebyshev’s inequality would imply
$\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]\sim \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]^2$
. Then Chebyshev’s inequality would imply
![]() ${\boldsymbol{Z}}\sim \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]$
w.h.p., and thus, in light of (2.1), that
${\boldsymbol{Z}}\sim \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]$
w.h.p., and thus, in light of (2.1), that
![]() $\mathbb{A} x={\boldsymbol{y}}$
has a solution w.h.p.
$\mathbb{A} x={\boldsymbol{y}}$
has a solution w.h.p.
Concerning the computation of
![]() $\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]$
, because the set of solutions is either empty or a translation of the kernel, we obtain
$\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]$
, because the set of solutions is either empty or a translation of the kernel, we obtain
 \begin{align} \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]&=\sum _{\sigma,\tau \in \mathbb{F}_q^n}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathbb{A}\sigma =\mathbb{A}\tau ={\boldsymbol{y}}}\right \rbrack =\sum _{\sigma,\tau \in \mathbb{F}_q^n}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathbb{A}\sigma ={\boldsymbol{y}}}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\sigma -\tau \in \ker \mathbb{A}}\right \rbrack \nonumber \\[5pt] &=\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}}\right \rbrack \mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|. \end{align}
\begin{align} \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2]&=\sum _{\sigma,\tau \in \mathbb{F}_q^n}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathbb{A}\sigma =\mathbb{A}\tau ={\boldsymbol{y}}}\right \rbrack =\sum _{\sigma,\tau \in \mathbb{F}_q^n}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathbb{A}\sigma ={\boldsymbol{y}}}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\sigma -\tau \in \ker \mathbb{A}}\right \rbrack \nonumber \\[5pt] &=\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}}\right \rbrack \mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|. \end{align}
To calculate the expected kernel size we notice that the probability that a vector
![]() $x$
is in the kernel depends on its Hamming weight. For instance, the zero vector always belongs to the kernel, while the all-ones vector
$x$
is in the kernel depends on its Hamming weight. For instance, the zero vector always belongs to the kernel, while the all-ones vector
![]() ${\mathbb{1}}$
does not w.h.p. More systematically, invoking inclusion/exclusion, we find that for a vector
${\mathbb{1}}$
does not w.h.p. More systematically, invoking inclusion/exclusion, we find that for a vector
![]() $x$
of Hamming weight
$x$
of Hamming weight
![]() $w$
we have
$w$
we have
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{x\in \ker \mathbb{A}}\right \rbrack \sim \left \lbrack{(1+(1-2w/n)^3)/2}\right \rbrack ^{{\boldsymbol{m}}}.$
Since the total number of such vectors comes to
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{x\in \ker \mathbb{A}}\right \rbrack \sim \left \lbrack{(1+(1-2w/n)^3)/2}\right \rbrack ^{{\boldsymbol{m}}}.$
Since the total number of such vectors comes to
![]() $\binom n{w}$
, we obtain
$\binom n{w}$
, we obtain
Taking logarithms, invoking Stirling’s formula and parametrising
![]() $w=z n$
, we simplify (2.3) to
$w=z n$
, we simplify (2.3) to
If we substitute
![]() $z=1/2$
into (2.4), the expression further simplifies to
$z=1/2$
into (2.4), the expression further simplifies to
![]() $(n-{\boldsymbol{m}})\log 2$
. Hence, if the maximum is attained at another value
$(n-{\boldsymbol{m}})\log 2$
. Hence, if the maximum is attained at another value
![]() $z\neq 1/2$
, then (2.4) yields
$z\neq 1/2$
, then (2.4) yields
![]() $\mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|\gg 2^{n-{\boldsymbol{m}}}$
and the second moment method fails.
$\mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|\gg 2^{n-{\boldsymbol{m}}}$
and the second moment method fails.
Figure 3 displays (2.4) for
![]() $d=2.5$
and
$d=2.5$
and
![]() $d=2.7$
. While for
$d=2.7$
. While for
![]() $d=2.5$
the function takes its maximum at
$d=2.5$
the function takes its maximum at
![]() $z=1/2$
, for
$z=1/2$
, for
![]() $d=2.7$
the maximum is attained at
$d=2.7$
the maximum is attained at
![]() $z\approx 0.085$
. However, the true random 3-XORSAT threshold is
$z\approx 0.085$
. However, the true random 3-XORSAT threshold is
![]() $d\approx 2.75$
[Reference Dubois and Mandler21]. Thus, the naive second moment calculation falls short of the real threshold.
$d\approx 2.75$
[Reference Dubois and Mandler21]. Thus, the naive second moment calculation falls short of the real threshold.

Figure 3. The r.h.s. of (2.4) for
![]() $d=2.5$
(blue) and
$d=2.5$
(blue) and
![]() $d=2.7$
(red) in the interval
$d=2.7$
(red) in the interval
![]() $[0,\frac 12]$
.
$[0,\frac 12]$
.
How so? The expression (2.4) does not determine the ‘likely’ but the expected size of the kernel, a value prone to large deviations effects. Indeed, because the number of vectors in the kernel scales exponentially with
![]() $n$
, an exponentially unlikely event that causes an exceptionally large kernel may end up dominating
$n$
, an exponentially unlikely event that causes an exceptionally large kernel may end up dominating
![]() $\mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|$
. Precisely such an event manifests itself in the left local maximum in Fig. 3. Moreover, as we approach the satisfiability threshold such large deviations issues are compounded by a diminishing error tolerance. Indeed, while for
$\mathbb{E}_{\mathfrak{A}}|\ker \mathbb{A}|$
. Precisely such an event manifests itself in the left local maximum in Fig. 3. Moreover, as we approach the satisfiability threshold such large deviations issues are compounded by a diminishing error tolerance. Indeed, while for
![]() $d=2.5$
the value at
$d=2.5$
the value at
![]() $z=1/2$
just swallows the spurious maximum, this is no longer the case for
$z=1/2$
just swallows the spurious maximum, this is no longer the case for
![]() $d=2.7$
.
$d=2.7$
.
For random
![]() $k$
-XORSAT Dubois and Mandler managed to identify the precise large deviations effect at work. It stems from fluctuations of a densely connected sub-graph of
$k$
-XORSAT Dubois and Mandler managed to identify the precise large deviations effect at work. It stems from fluctuations of a densely connected sub-graph of
![]() $\mathbb{G}$
called the 2-core, obtained by iteratively pruning nodes of degree less than two along with their neighbours (if any). Dubois and Mandler pinpointed the 3-XORSAT threshold by applying the second moment method to the minor
$\mathbb{G}$
called the 2-core, obtained by iteratively pruning nodes of degree less than two along with their neighbours (if any). Dubois and Mandler pinpointed the 3-XORSAT threshold by applying the second moment method to the minor
![]() $\mathbb{A}^{(2)}$
induced by
$\mathbb{A}^{(2)}$
induced by
![]() ${\mathbb{G}}^{(2)}$
while conditioning on the 2-core having its typical dimensions.
${\mathbb{G}}^{(2)}$
while conditioning on the 2-core having its typical dimensions.
The technical difficulty is that the rows of
![]() $\mathbb{A}^{(2)}$
are no longer independent. Indeed,
$\mathbb{A}^{(2)}$
are no longer independent. Indeed,
![]() $\mathbb{A}^{(2)}$
is distributed as a random matrix with a truncated Poisson
$\mathbb{A}^{(2)}$
is distributed as a random matrix with a truncated Poisson
![]() ${\boldsymbol{d}}^{(2)}\sim \text{Po}_{\geq 2}(d')$
with
${\boldsymbol{d}}^{(2)}\sim \text{Po}_{\geq 2}(d')$
with
![]() $d'=d'(d,k)\gt 0$
as the distribution of the variable degrees. Unfortunately, the given-degrees model leads to a fairly complicated moment computation. Instead of the humble one-dimensional problem from (2.4) we now face parameters
$d'=d'(d,k)\gt 0$
as the distribution of the variable degrees. Unfortunately, the given-degrees model leads to a fairly complicated moment computation. Instead of the humble one-dimensional problem from (2.4) we now face parameters
![]() $(z_i)_{i\geq 2}$
that gauge the fraction of variables of each possible degree
$(z_i)_{i\geq 2}$
that gauge the fraction of variables of each possible degree
![]() $i$
set to one. Additionally, on the constraint side we need to keep track of the number of equations with zero and with two variables set to one. Of course, these variables are tied together through the constraint that the total Hamming weight on the variable side matches that on the constraint side.
$i$
set to one. Additionally, on the constraint side we need to keep track of the number of equations with zero and with two variables set to one. Of course, these variables are tied together through the constraint that the total Hamming weight on the variable side matches that on the constraint side.
With a deal of diligence Dubois and Mandler managed to solve this optimisation problem. However, even just the step on to check degrees
![]() $k\gt 3$
turns out to be tricky because now we need to keep track of all the possible ways in which a
$k\gt 3$
turns out to be tricky because now we need to keep track of all the possible ways in which a
![]() $k$
-ary parity constraint can be satisfied [Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Pittel44]. Yet even these difficulties are eclipsed by those that result from merely advancing to fields of size
$k$
-ary parity constraint can be satisfied [Reference Dietzfelbinger, Goerdt, Mitzenmacher, Montanari, Pagh and Rink19, Reference Pittel44]. Yet even these difficulties are eclipsed by those that result from merely advancing to fields of size
![]() $q=3$
[Reference Goerdt and Falke23].
$q=3$
[Reference Goerdt and Falke23].
Not to mention entirely general degree distributions
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
and general fields
${\boldsymbol{d}},{\boldsymbol{k}}$
and general fields
![]() $\mathbb{F}_q$
as in Theorem 1.1. The ensuing optimisation problem comes in terms of variables
$\mathbb{F}_q$
as in Theorem 1.1. The ensuing optimisation problem comes in terms of variables
![]() $(z_i)_{i\in{\text{supp}}{\boldsymbol{d}}}$
that range over the space
$(z_i)_{i\in{\text{supp}}{\boldsymbol{d}}}$
that range over the space
![]() $\mathcal{P}(\mathbb{F}_q)$
of probability distributions on
$\mathcal{P}(\mathbb{F}_q)$
of probability distributions on
![]() $\mathbb{F}_q$
. Additionally, there is a second set of variables
$\mathbb{F}_q$
. Additionally, there is a second set of variables
![]() $(\hat z_{\chi _1,\ldots,\chi _\ell })_{\ell \in{\text{supp}}{\boldsymbol{k}},\,\chi _1,\ldots,\chi _\ell \in{\text{supp}}\boldsymbol{\chi }}$
to go with the rows of
$(\hat z_{\chi _1,\ldots,\chi _\ell })_{\ell \in{\text{supp}}{\boldsymbol{k}},\,\chi _1,\ldots,\chi _\ell \in{\text{supp}}\boldsymbol{\chi }}$
to go with the rows of
![]() $\mathbb{A}$
whose non-zero entries are precisely
$\mathbb{A}$
whose non-zero entries are precisely
![]() $\chi _1,\ldots,\chi _\ell$
. These variables range over probability distributions on solutions
$\chi _1,\ldots,\chi _\ell$
. These variables range over probability distributions on solutions
![]() $\sigma \in \mathbb{F}_q^\ell$
to
$\sigma \in \mathbb{F}_q^\ell$
to
![]() $\chi _1\sigma _1+\cdots +\chi _\ell \sigma _\ell =0$
. In terms of these variables we would need to solve
$\chi _1\sigma _1+\cdots +\chi _\ell \sigma _\ell =0$
. In terms of these variables we would need to solve
 \begin{align} &\max \sum _{\sigma \in \mathbb{F}_q}\mathbb{E}\left \lbrack{({\boldsymbol{d}}-1)z_{{\boldsymbol{d}}}(\sigma )\log z_{{\boldsymbol{d}}}(\sigma )}\right \rbrack \nonumber\\[5pt] &\quad -\frac{d}{k}\mathbb{E}\left \lbrack{\sum _{\substack{\sigma _1,\dots,\sigma _{{\boldsymbol{k}}}\in \mathbb{F}_q\\ {\boldsymbol{\chi }_{1,1}\sigma _1+\cdots +\boldsymbol{\chi }_{1,{\boldsymbol{k}}}\sigma _{{\boldsymbol{k}}}=0}}}\hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})\log \hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})}\right \rbrack \\[5pt] &\quad \mbox{s.t.}\quad \mathbb{E}[{\boldsymbol{d}} z_{{\boldsymbol{d}}}(\tau )]=\mathbb{E}\left \lbrack{\sum _{\substack{\sigma _1,\dots,\sigma _{{\boldsymbol{k}}}\in \mathbb{F}_q\\ {\boldsymbol{\chi }_{1,1}\sigma _1+\cdots +\boldsymbol{\chi }_{1,{\boldsymbol{k}}}\sigma _{{\boldsymbol{k}}}=0}}}{\boldsymbol{k}}{\mathbb{1}}\left \{{\sigma _1=\tau }\right \}\hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})}\right \rbrack \quad \mbox{for all }\tau \in \mathbb{F}_q\nonumber . \end{align}
\begin{align} &\max \sum _{\sigma \in \mathbb{F}_q}\mathbb{E}\left \lbrack{({\boldsymbol{d}}-1)z_{{\boldsymbol{d}}}(\sigma )\log z_{{\boldsymbol{d}}}(\sigma )}\right \rbrack \nonumber\\[5pt] &\quad -\frac{d}{k}\mathbb{E}\left \lbrack{\sum _{\substack{\sigma _1,\dots,\sigma _{{\boldsymbol{k}}}\in \mathbb{F}_q\\ {\boldsymbol{\chi }_{1,1}\sigma _1+\cdots +\boldsymbol{\chi }_{1,{\boldsymbol{k}}}\sigma _{{\boldsymbol{k}}}=0}}}\hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})\log \hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})}\right \rbrack \\[5pt] &\quad \mbox{s.t.}\quad \mathbb{E}[{\boldsymbol{d}} z_{{\boldsymbol{d}}}(\tau )]=\mathbb{E}\left \lbrack{\sum _{\substack{\sigma _1,\dots,\sigma _{{\boldsymbol{k}}}\in \mathbb{F}_q\\ {\boldsymbol{\chi }_{1,1}\sigma _1+\cdots +\boldsymbol{\chi }_{1,{\boldsymbol{k}}}\sigma _{{\boldsymbol{k}}}=0}}}{\boldsymbol{k}}{\mathbb{1}}\left \{{\sigma _1=\tau }\right \}\hat z_{\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,{\boldsymbol{k}}}}(\sigma _1,\ldots,\sigma _{{\boldsymbol{k}}})}\right \rbrack \quad \mbox{for all }\tau \in \mathbb{F}_q\nonumber . \end{align}
On an high level, (2.5) is not so different from (2.4): The first summand in (2.5) corresponds to the number of vectors with a specified number of components of each field element, taking into account the different numbers of non-zero entries of the columns. The remaining part corresponds to the probability that any such vector satisfies all equations, taking into account the number of field elements of each type in a random equation. Finally, while the frequencies of the field elements appear decoupled for rows and columns in the first line of (2.5), the second line ensures that only compatible frequencies are considered after all. As in random 3-XORSAT, a simple calculation shows that the value of (2.5) evaluated at the ‘equitable’ solution
hits the value
![]() $(1-d/k)\log q$
, which matches the normalised first moment
$(1-d/k)\log q$
, which matches the normalised first moment
![]() $n^{-1}\log \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]$
.
$n^{-1}\log \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]$
.
In summary, the second moment method hardly seems like a promising path towards Theorem 1.1. Not only does (2.5) seem unwieldy as even for very special cases of
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
an analytic solution remains elusive [Reference Goerdt and Falke23]. Even worse, just in the case of ‘unabridged’ random
${\boldsymbol{d}},{\boldsymbol{k}}$
an analytic solution remains elusive [Reference Goerdt and Falke23]. Even worse, just in the case of ‘unabridged’ random
![]() $k$
-XORSAT large deviations effects may cause spurious maxima. In effect, even if we could miraculously figure out the precise conditions for (2.5) being attained at the uniform solution, this would hardly determine for what
$k$
-XORSAT large deviations effects may cause spurious maxima. In effect, even if we could miraculously figure out the precise conditions for (2.5) being attained at the uniform solution, this would hardly determine for what
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
the random matrix
${\boldsymbol{d}},{\boldsymbol{k}}$
the random matrix
![]() $\mathbb{A}$
actually has full row rank w.h.p.
$\mathbb{A}$
actually has full row rank w.h.p.
2.2 Quenching and truncating
The large deviations issues ultimately result from our attempt at computing the mean of
![]() $|\ker \mathbb{A}|$
, a (potentially) exponential quantity. The mathematical physics prescription is to compute the expectation of its logarithm instead [Reference Mézard40]. In the present algebraic setting this comes down to computing the mean of the nullity
$|\ker \mathbb{A}|$
, a (potentially) exponential quantity. The mathematical physics prescription is to compute the expectation of its logarithm instead [Reference Mézard40]. In the present algebraic setting this comes down to computing the mean of the nullity
![]() $\text{nul}\mathbb{A}=\dim \ker \mathbb{A}$
, or equivalently of the rank
$\text{nul}\mathbb{A}=\dim \ker \mathbb{A}$
, or equivalently of the rank
![]() ${\text{rk}}\mathbb{A}=n-\text{nul}\mathbb{A}$
. This ‘quenched average’ is always of order
${\text{rk}}\mathbb{A}=n-\text{nul}\mathbb{A}$
. This ‘quenched average’ is always of order
![]() $O(n)$
and therefore immune to large deviations effects. In fact, even if on some unfortunate event of exponentially small probability
$O(n)$
and therefore immune to large deviations effects. In fact, even if on some unfortunate event of exponentially small probability
![]() $\exp\!(-\Omega (n))$
the kernel of
$\exp\!(-\Omega (n))$
the kernel of
![]() $\mathbb{A}$
were quite large, the ensuing boost to
$\mathbb{A}$
were quite large, the ensuing boost to
![]() $\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
remains negligible.
$\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
remains negligible.
Yet computing the quenched average
![]() $\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
does not suffice to prove Theorem 1.1. Indeed, (1.4) already provides an asymptotic formula for
$\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
does not suffice to prove Theorem 1.1. Indeed, (1.4) already provides an asymptotic formula for
![]() $\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
. But as we saw due to the normalisation on the l.h.s. (1.4) merely implies that
$\mathbb{E}_{\mathfrak{A}}[\text{nul}\mathbb{A}]$
. But as we saw due to the normalisation on the l.h.s. (1.4) merely implies that
![]() ${\text{rk}}\mathbb{A}={\boldsymbol{m}}-o(n)$
w.h.p. To actually prove that
${\text{rk}}\mathbb{A}={\boldsymbol{m}}-o(n)$
w.h.p. To actually prove that
![]() ${\text{rk}}\mathbb{A}={\boldsymbol{m}}$
w.h.p. we will combine the quenched computation with a truncated moment argument calculation. Specifically, we will harness an enhanced version of (1.4) to prove that under the assumptions of Theorem 1.1 the only combinatorially meaningful solutions to (2.5) asymptotically coincide with the equitable solution (2.6), around which we will subsequently expand (2.5) carefully.
${\text{rk}}\mathbb{A}={\boldsymbol{m}}$
w.h.p. we will combine the quenched computation with a truncated moment argument calculation. Specifically, we will harness an enhanced version of (1.4) to prove that under the assumptions of Theorem 1.1 the only combinatorially meaningful solutions to (2.5) asymptotically coincide with the equitable solution (2.6), around which we will subsequently expand (2.5) carefully.
To carry this programme out, let
![]() ${\boldsymbol{x}}_{\mathbb{A}}=({\boldsymbol{x}}_{\mathbb{A},i})_{i\in [n]}\in \mathbb{F}_q^n$
be a random vector from the kernel of
${\boldsymbol{x}}_{\mathbb{A}}=({\boldsymbol{x}}_{\mathbb{A},i})_{i\in [n]}\in \mathbb{F}_q^n$
be a random vector from the kernel of
![]() $\mathbb{A}$
. Consider the event
$\mathbb{A}$
. Consider the event
 \begin{align} {\mathfrak{O}}&={\left \{{A \;:\; \sum _{\sigma,\tau \in \mathbb{F}_q}\sum _{i,j=1}^n\left |{{\mathbb{P}}\left \lbrack{{\boldsymbol{x}}_{A,i}=\sigma,\ {\boldsymbol{x}}_{A,j}=\tau \mid A}\right \rbrack -q^{-2}}\right |=o(n^2)}\right \}.} \end{align}
\begin{align} {\mathfrak{O}}&={\left \{{A \;:\; \sum _{\sigma,\tau \in \mathbb{F}_q}\sum _{i,j=1}^n\left |{{\mathbb{P}}\left \lbrack{{\boldsymbol{x}}_{A,i}=\sigma,\ {\boldsymbol{x}}_{A,j}=\tau \mid A}\right \rbrack -q^{-2}}\right |=o(n^2)}\right \}.} \end{align}
Then by Chebyshev’s inequality on
![]() $\mathfrak{O}$
w.h.p. we have
$\mathfrak{O}$
w.h.p. we have
Hence, on
![]() $\mathfrak{O}$
the only combinatorially relevant value of
$\mathfrak{O}$
the only combinatorially relevant value of
![]() $z_\ell (\sigma )$
from (2.5) is the uniform
$z_\ell (\sigma )$
from (2.5) is the uniform
![]() $1/q$
for every
$1/q$
for every
![]() $\ell,\sigma$
, because for every
$\ell,\sigma$
, because for every
![]() $\ell$
asymptotically almost all kernel vectors set about an equal number of variables of degree
$\ell$
asymptotically almost all kernel vectors set about an equal number of variables of degree
![]() $\ell$
to each of the
$\ell$
to each of the
![]() $q$
possible values. Thanks to this observation will prove that w.h.p.
$q$
possible values. Thanks to this observation will prove that w.h.p.
provided that (1.3) is satisfied. Theorem (1.1) will turn out to be an easy consequence of (2.8)–(2.9) and Corollary 1.2 of Theorem 1.1.
Thus, the challenge is to prove (2.8)–(2.9). Specifically, while the second asymptotic equality in (2.8) is easy, the proof of the first is where we require knowledge of the ‘quenched average’ (1.4). In fact, instead of just applying (1.4) as is we will need to perform a ‘quenched’ computation for a slightly enhanced random matrix from scratch. Second, the key challenge towards the proof of (2.9) is to obtain an exact asymptotic equality here, rather than the weaker estimate
![]() $\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}^2\cdot {\mathbb{1}}\left \{{\mathbb{A}\in \mathfrak{O}}\right \}}\right \rbrack =O(\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}}\right \rbrack ^2)$
. This will require a meticulous expansion of the second moment around the uniform solution, which will involve the detailed analysis of the lattices generated by integer vectors that encode conceivable values of
$\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}^2\cdot {\mathbb{1}}\left \{{\mathbb{A}\in \mathfrak{O}}\right \}}\right \rbrack =O(\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}}\right \rbrack ^2)$
. This will require a meticulous expansion of the second moment around the uniform solution, which will involve the detailed analysis of the lattices generated by integer vectors that encode conceivable values of
![]() $z_i,\hat z_{\chi _1, \ldots, \chi _\ell }$
from (2.5).
$z_i,\hat z_{\chi _1, \ldots, \chi _\ell }$
from (2.5).
2.3
Specified
 $d_1,\ldots,d_n$
and
$d_1,\ldots,d_n$
and
 $k_1,\ldots,k_m$
$k_1,\ldots,k_m$
Given two positive integers
![]() $n$
and
$n$
and
![]() $m=m(n)$
, consider now two arrays
$m=m(n)$
, consider now two arrays
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
of non-negative integers such that for all
$(k_i^{(m)})_{1 \leq i \leq m}$
of non-negative integers such that for all
![]() $n$
,
$n$
,
 \begin{equation*}\sum _{i=1}^n d_i^{(n)}=\sum _{j=1}^m k_j^{(m)}.\end{equation*}
\begin{equation*}\sum _{i=1}^n d_i^{(n)}=\sum _{j=1}^m k_j^{(m)}.\end{equation*}
We aim to find conditions on the arrays
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
and the sequence
$(k_i^{(m)})_{1 \leq i \leq m}$
and the sequence
![]() $(m(n))_{n \geq 1}$
which guarantee full row rank for the corresponding matrix in this fixed-degree setting as
$(m(n))_{n \geq 1}$
which guarantee full row rank for the corresponding matrix in this fixed-degree setting as
![]() $n \to \infty$
and are analogous to (1.3). Throughout, we abbreviate
$n \to \infty$
and are analogous to (1.3). Throughout, we abbreviate
![]() $m(n)= m$
. Let
$m(n)= m$
. Let
![]() ${\boldsymbol{d}}_n$
denote a uniformly chosen element from the sequence
${\boldsymbol{d}}_n$
denote a uniformly chosen element from the sequence
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() ${\boldsymbol{k}}_n$
a uniformly chosen element from the sequence
${\boldsymbol{k}}_n$
a uniformly chosen element from the sequence
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
. Assume that
$(k_i^{(m)})_{1 \leq i \leq m}$
. Assume that
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
satisfy the following conditions in terms of the uniformly chosen degrees
$(k_i^{(m)})_{1 \leq i \leq m}$
satisfy the following conditions in terms of the uniformly chosen degrees
![]() ${\boldsymbol{d}}_n$
and
${\boldsymbol{d}}_n$
and
![]() ${\boldsymbol{k}}_n$
:
${\boldsymbol{k}}_n$
:
-
(P1) There exist (integer-valued) random variables
 ${\boldsymbol{d}}, {\boldsymbol{k}} \geq 0$
with
${\boldsymbol{d}}, {\boldsymbol{k}} \geq 0$
with
 ${\mathbb{P}}({\boldsymbol{d}} =0)\lt 1$
and
${\mathbb{P}}({\boldsymbol{d}} =0)\lt 1$
and
 ${\mathbb{P}}({\boldsymbol{k}} \geq 3)=1$
such that
${\mathbb{P}}({\boldsymbol{k}} \geq 3)=1$
such that
 ${\boldsymbol{d}}_n\stackrel{d}{\longrightarrow } {\boldsymbol{d}}$
and
${\boldsymbol{d}}_n\stackrel{d}{\longrightarrow } {\boldsymbol{d}}$
and
 ${\boldsymbol{k}}_n\stackrel{d}{\longrightarrow } {\boldsymbol{k}}$
;
${\boldsymbol{k}}_n\stackrel{d}{\longrightarrow } {\boldsymbol{k}}$
; -
(P2)
 $\mathbb{E}[{\boldsymbol{d}}], \mathbb{E}[{\boldsymbol{k}}] \lt \infty$
and
$\mathbb{E}[{\boldsymbol{d}}], \mathbb{E}[{\boldsymbol{k}}] \lt \infty$
and
 $\mathbb{E}[{\boldsymbol{d}}_n] \to \mathbb{E}[{\boldsymbol{d}}]$
,
$\mathbb{E}[{\boldsymbol{d}}_n] \to \mathbb{E}[{\boldsymbol{d}}]$
,
 $\mathbb{E}[{\boldsymbol{k}}_n] \to \mathbb{E}[{\boldsymbol{k}}]$
as
$\mathbb{E}[{\boldsymbol{k}}_n] \to \mathbb{E}[{\boldsymbol{k}}]$
as
 $n \to \infty$
.
$n \to \infty$
. -
(P3)
 $\mathbb{E}[{\boldsymbol{d}}^2], \mathbb{E}[{\boldsymbol{k}}^2] \lt \infty$
and
$\mathbb{E}[{\boldsymbol{d}}^2], \mathbb{E}[{\boldsymbol{k}}^2] \lt \infty$
and
 $\mathbb{E}[{\boldsymbol{d}}_n^2] \to \mathbb{E}[{\boldsymbol{d}}^2]$
,
$\mathbb{E}[{\boldsymbol{d}}_n^2] \to \mathbb{E}[{\boldsymbol{d}}^2]$
,
 $\mathbb{E}[{\boldsymbol{k}}_n^2] \to \mathbb{E}[{\boldsymbol{k}}^2]$
as
$\mathbb{E}[{\boldsymbol{k}}_n^2] \to \mathbb{E}[{\boldsymbol{k}}^2]$
as
 $n \to \infty$
.
$n \to \infty$
. -
(P4) For some
 $\eta \gt 0$
,
$\eta \gt 0$
,
 $\mathbb{E}[{\boldsymbol{d}}^{2+\eta }] \lt \infty$
and
$\mathbb{E}[{\boldsymbol{d}}^{2+\eta }] \lt \infty$
and
 $\mathbb{E}[{\boldsymbol{d}}_n^{2+\eta }] \to \mathbb{E}[{\boldsymbol{d}}^{2+\eta }]$
.
$\mathbb{E}[{\boldsymbol{d}}_n^{2+\eta }] \to \mathbb{E}[{\boldsymbol{d}}^{2+\eta }]$
. -
(P5)
 $m \sim \mathbb{E}\left \lbrack{{\boldsymbol{d}}}\right \rbrack n/ \mathbb{E}\left \lbrack{{\boldsymbol{k}}}\right \rbrack$
.
$m \sim \mathbb{E}\left \lbrack{{\boldsymbol{d}}}\right \rbrack n/ \mathbb{E}\left \lbrack{{\boldsymbol{k}}}\right \rbrack$
. -
(P6) For all
 $m$
and
$m$
and
 $j \in [m]$
,
$j \in [m]$
,
 $k_j^{(m)}\ge 3$
.
$k_j^{(m)}\ge 3$
. -
(P7) For all
 $n$
,
$n$
,
 $\gcd ({\text{supp}}({\boldsymbol{d}}))=\gcd (d_i^{(n)})_{1 \leq i \leq n})$
.
$\gcd ({\text{supp}}({\boldsymbol{d}}))=\gcd (d_i^{(n)})_{1 \leq i \leq n})$
.
Conditions (P1)-(P3) correspond to standard regularity conditions for the non-bipartite version of the configuration model (see Condition 7.8 in [Reference van der Hofstad25], for example).
Let
![]() $D(x)$
and
$D(x)$
and
![]() $K(x)$
denote the probability generating functions for
$K(x)$
denote the probability generating functions for
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
, respectively. We also abbreviate
${\boldsymbol{k}}$
, respectively. We also abbreviate
![]() $d=\mathbb{E}\left \lbrack{{\boldsymbol{d}}}\right \rbrack$
and
$d=\mathbb{E}\left \lbrack{{\boldsymbol{d}}}\right \rbrack$
and
![]() $k=\mathbb{E}\left \lbrack{{\boldsymbol{k}}}\right \rbrack$
as before. We may then define
$k=\mathbb{E}\left \lbrack{{\boldsymbol{k}}}\right \rbrack$
as before. We may then define
Finally, to make the difference to the i.i.d. degree case apparent, we denote the random matrix constructed by generating a uniformly random simple Tanner graph based on the fixed-degree sequences
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
by
$(k_i^{(m)})_{1 \leq i \leq m}$
by
![]() $\underline{\mathbb{A}}$
. Again, the non-zero entries of
$\underline{\mathbb{A}}$
. Again, the non-zero entries of
![]() $\underline{\mathbb{A}}$
are i.i.d. copies of the random variable
$\underline{\mathbb{A}}$
are i.i.d. copies of the random variable
![]() $\boldsymbol{\chi }$
.
$\boldsymbol{\chi }$
.
Proposition 2.1.
Suppose that
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
satisfy
$(k_i^{(m)})_{1 \leq i \leq m}$
satisfy
![]() $\sum _{i=1}^n d_i^{(n)}=\sum _{j=1}^m k_j^{(n)}$
for all
$\sum _{i=1}^n d_i^{(n)}=\sum _{j=1}^m k_j^{(n)}$
for all
![]() $n$
and properties (P1)-(P7). Let
$n$
and properties (P1)-(P7). Let
![]() $\mathfrak{d}=\gcd ({\text{supp}}({\boldsymbol{d}}))$
. If
$\mathfrak{d}=\gcd ({\text{supp}}({\boldsymbol{d}}))$
. If
![]() $q$
and
$q$
and
![]() $\mathfrak{d}$
are coprime, and
$\mathfrak{d}$
are coprime, and
-
(a)
 $\underline{\mathbb{A}}\in \mathfrak{O}$
w.h.p.;
$\underline{\mathbb{A}}\in \mathfrak{O}$
w.h.p.;
-
(b)
 $\Phi (z)\lt \Phi (0)$
for all
$\Phi (z)\lt \Phi (0)$
for all
 $0\lt z\leq 1$
;
$0\lt z\leq 1$
;
then
![]() $\underline{\mathbb{A}}$
has full row rank over
$\underline{\mathbb{A}}$
has full row rank over
![]() $\mathbb{F}_q$
w.h.p.
$\mathbb{F}_q$
w.h.p.
Remark 2.2. As mentioned above, conditions (P1)-(P3) are natural when considering the configuration model on general specified degree sequences
![]() $(d_i^{(n)})_{1\leq i\leq n}$
and
$(d_i^{(n)})_{1\leq i\leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
. In particular, these are sufficient and necessary conditions to allow translation of results from the pairing model. A more detailed discussion and references can be found below Lemma 3.6. Conditions (P4) and (P7) are needed in the proof of a local limit theorem for the random vector
$(k_i^{(m)})_{1 \leq i \leq m}$
. In particular, these are sufficient and necessary conditions to allow translation of results from the pairing model. A more detailed discussion and references can be found below Lemma 3.6. Conditions (P4) and (P7) are needed in the proof of a local limit theorem for the random vector
![]() $\rho _{\boldsymbol{\sigma }} \in \mathbb{Z}^{\mathbb{F}_q}$
, where
$\rho _{\boldsymbol{\sigma }} \in \mathbb{Z}^{\mathbb{F}_q}$
, where
![]() $\rho _{\boldsymbol{\sigma }}(s)\;:\!=\;\sum _{i=1}^n d_i {\mathbb{1}}{\{\boldsymbol{\sigma }_i=s\}}$
for a uniformly random
$\rho _{\boldsymbol{\sigma }}(s)\;:\!=\;\sum _{i=1}^n d_i {\mathbb{1}}{\{\boldsymbol{\sigma }_i=s\}}$
for a uniformly random
![]() $\boldsymbol{\sigma }\in \mathbb{F}_q^n$
and
$\boldsymbol{\sigma }\in \mathbb{F}_q^n$
and
![]() $s\in \mathbb{F}_q$
. While
$s\in \mathbb{F}_q$
. While
![]() $m=\Theta (n)$
is essential throughout the whole proof, the precise asymptotics in (P5) are only used in the final conclusion in the proof of Proposition 2.1. Finally, we chiefly employ condition (P6) in the proof of Claim 7.12.
$m=\Theta (n)$
is essential throughout the whole proof, the precise asymptotics in (P5) are only used in the final conclusion in the proof of Proposition 2.1. Finally, we chiefly employ condition (P6) in the proof of Claim 7.12.
We first prove Proposition 2.1. Then, we prove Theorem 1.1 by showing that w.h.p.
![]() $\mathbb{A}\in \mathfrak{O}$
if
$\mathbb{A}\in \mathfrak{O}$
if
![]() ${\boldsymbol{m}} \sim \text{Po}(dn/k)$
,
${\boldsymbol{m}} \sim \text{Po}(dn/k)$
,
![]() $({\boldsymbol{d}}_i)_{i \geq 1}$
and
$({\boldsymbol{d}}_i)_{i \geq 1}$
and
![]() $({\boldsymbol{k}}_j)_{j \geq 1}$
are i.i.d. copies of
$({\boldsymbol{k}}_j)_{j \geq 1}$
are i.i.d. copies of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
. Theorem 1.1 then follows from Proposition 2.1.
${\boldsymbol{k}}$
. Theorem 1.1 then follows from Proposition 2.1.
In the current case,
![]() $\mathfrak{A}$
simply is the
$\mathfrak{A}$
simply is the
![]() $\sigma$
-algebra generated by the numbers
$\sigma$
-algebra generated by the numbers
![]() ${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of equations of degree
${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of equations of degree
![]() $\ell \geq 3$
with coefficients
$\ell \geq 3$
with coefficients
![]() $\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
, since all degrees are deterministic. When
$\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
, since all degrees are deterministic. When
![]() $\mathfrak{A}$
is used as a subscript, it serves as a notation that suppresses explicit mentioning of
$\mathfrak{A}$
is used as a subscript, it serves as a notation that suppresses explicit mentioning of
![]() $m$
,
$m$
,
![]() $(d_i^{(n)})_{i=1}^n$
and
$(d_i^{(n)})_{i=1}^n$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
. As discussed above, it suffices to prove (2.8) (with
$(k_i^{(m)})_{1 \leq i \leq m}$
. As discussed above, it suffices to prove (2.8) (with
![]() ${\boldsymbol{m}}=m$
) and (2.9) in the more general model
${\boldsymbol{m}}=m$
) and (2.9) in the more general model
![]() $\underline{\mathbb{A}}$
. We observe that (2.8) follows immediately by hypothesis (a) of Proposition 2.1, as w.h.p.,
$\underline{\mathbb{A}}$
. We observe that (2.8) follows immediately by hypothesis (a) of Proposition 2.1, as w.h.p.,
 \begin{align} &\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}\cdot {\mathbb{1}}\left \{{\underline{\mathbb{A}}\in \mathfrak{O}}\right \}}\right \rbrack \nonumber \\[5pt] &\quad =\sum _{A\in \mathfrak{O}} \sum _{\sigma \in \mathbb{F}^n} \sum _{y\in \mathbb{F}^m}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\underline{\mathbb{A}}=A,{\boldsymbol{y}}=y}\right \rbrack {\mathbb{1}}\left \{{A\sigma =y}\right \} = q^{n-m} \sum _{A\in \mathfrak{O}}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\underline{\mathbb{A}}=A}\right \rbrack \sim q^{n-m}. \end{align}
\begin{align} &\mathbb{E}_{\mathfrak{A}}\left \lbrack{{\boldsymbol{Z}}\cdot {\mathbb{1}}\left \{{\underline{\mathbb{A}}\in \mathfrak{O}}\right \}}\right \rbrack \nonumber \\[5pt] &\quad =\sum _{A\in \mathfrak{O}} \sum _{\sigma \in \mathbb{F}^n} \sum _{y\in \mathbb{F}^m}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\underline{\mathbb{A}}=A,{\boldsymbol{y}}=y}\right \rbrack {\mathbb{1}}\left \{{A\sigma =y}\right \} = q^{n-m} \sum _{A\in \mathfrak{O}}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\underline{\mathbb{A}}=A}\right \rbrack \sim q^{n-m}. \end{align}
Thus, to complete the proof for Proposition 2.1 it suffices to prove (2.9).
2.4 The truncated first moment
We start our discussion by verifying condition (a) of Proposition 2.1 for i.i.d.
![]() ${\boldsymbol{d}}_i$
and
${\boldsymbol{d}}_i$
and
![]() ${\boldsymbol{k}}_j$
. Hence, let us restrict to the ‘i.i.d. version’ of
${\boldsymbol{k}}_j$
. Hence, let us restrict to the ‘i.i.d. version’ of
![]() $\mathbb{A}$
, that is,
$\mathbb{A}$
, that is,
![]() ${\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n$
and
${\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n$
and
![]() ${\boldsymbol{k}}_1,\ldots, {\boldsymbol{k}}_{{\boldsymbol{m}}}$
are i.i.d. copies of
${\boldsymbol{k}}_1,\ldots, {\boldsymbol{k}}_{{\boldsymbol{m}}}$
are i.i.d. copies of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
. Although we know the approximate nullity (1.4) of
${\boldsymbol{k}}$
. Although we know the approximate nullity (1.4) of
![]() $\mathbb{A}$
already, this does not suffice to actually prove that
$\mathbb{A}$
already, this does not suffice to actually prove that
![]() $\mathfrak{O}$
is a ‘likely’ event. To this end we need to study a slightly modified matrix instead. Specifically, for an integer
$\mathfrak{O}$
is a ‘likely’ event. To this end we need to study a slightly modified matrix instead. Specifically, for an integer
![]() $t\geq 0$
obtain
$t\geq 0$
obtain
![]() $\mathbb{A}_{[t]}$
from
$\mathbb{A}_{[t]}$
from
![]() $\mathbb{A}$
by adding
$\mathbb{A}$
by adding
![]() $t$
more rows that contain precisely three non-zero entries. The positions of these non-zero entries are chosen uniformly, mutually independently and independently of everything else, and the non-zero entries themselves are independent copies of
$t$
more rows that contain precisely three non-zero entries. The positions of these non-zero entries are chosen uniformly, mutually independently and independently of everything else, and the non-zero entries themselves are independent copies of
![]() $\boldsymbol{\chi }$
. We require the following lower bound on the rank of
$\boldsymbol{\chi }$
. We require the following lower bound on the rank of
![]() $\mathbb{A}_{[t]}$
.
$\mathbb{A}_{[t]}$
.
Proposition 2.3.
If (1.3) is satisfied then there exists
![]() $\delta _0=\delta _0({\boldsymbol{d}},{\boldsymbol{k}})\gt 0$
such that for all
$\delta _0=\delta _0({\boldsymbol{d}},{\boldsymbol{k}})\gt 0$
such that for all
![]() $0\lt \delta \lt \delta _0$
we have
$0\lt \delta \lt \delta _0$
we have
The proof of Proposition 2.3 relies on the Aizenman-Sims-Starr scheme, a coupling argument inspired by spin glass theory [Reference Aizenman, Sims and Starr5]. The technique was also used in ref. [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] to prove the rank formula (1.4). While we mostly follow that proof strategy and can even reuse some of the intermediate deliberations, a subtle modification is required to accommodate the additional ternary equations. The details can be found in Section 4.
How does Proposition 2.3 facilitate the proof of (2.8)? Assuming (1.3), we obtain from (1.4) that
![]() $\text{nul}\mathbb{A}/n\sim 1-d/k$
w.h.p. Hence, (2.12) shows that nearly each one of the additional ternary rows added to
$\text{nul}\mathbb{A}/n\sim 1-d/k$
w.h.p. Hence, (2.12) shows that nearly each one of the additional ternary rows added to
![]() $\mathbb{A}_{\left \lbrack{\lfloor \delta n\rfloor }\right \rbrack }$
reduces the nullity. We are going to argue that this is possible only if
$\mathbb{A}_{\left \lbrack{\lfloor \delta n\rfloor }\right \rbrack }$
reduces the nullity. We are going to argue that this is possible only if
![]() $\mathbb{A}\in \mathfrak{O}$
w.h.p.
$\mathbb{A}\in \mathfrak{O}$
w.h.p.
To see this, let us think about the kernel of a general
![]() $M\times N$
matrix
$M\times N$
matrix
![]() $A$
over
$A$
over
![]() $\mathbb{F}_q$
for a short moment. Draw
$\mathbb{F}_q$
for a short moment. Draw
![]() ${\boldsymbol{x}}_A=({\boldsymbol{x}}_{A,i})_{i\in [N]}\in \ker A$
uniformly at random. For any given coordinate
${\boldsymbol{x}}_A=({\boldsymbol{x}}_{A,i})_{i\in [N]}\in \ker A$
uniformly at random. For any given coordinate
![]() ${\boldsymbol{x}}_{A,i}$
,
${\boldsymbol{x}}_{A,i}$
,
![]() $i\in [N]$
there are two possible scenarios: either
$i\in [N]$
there are two possible scenarios: either
![]() ${\boldsymbol{x}}_{A,i}=0$
deterministically, or
${\boldsymbol{x}}_{A,i}=0$
deterministically, or
![]() ${\boldsymbol{x}}_{A,i}$
is uniformly distributed over
${\boldsymbol{x}}_{A,i}$
is uniformly distributed over
![]() $\mathbb{F}_q$
. (This is because if we multiply
$\mathbb{F}_q$
. (This is because if we multiply
![]() ${\boldsymbol{x}}_A$
by a scalar
${\boldsymbol{x}}_A$
by a scalar
![]() $t\in \mathbb{F}_q$
we obtain
$t\in \mathbb{F}_q$
we obtain
![]() $t{\boldsymbol{x}}_A\in \ker A$
.) We therefore call coordinate
$t{\boldsymbol{x}}_A\in \ker A$
.) We therefore call coordinate
![]() $i$
frozen if
$i$
frozen if
![]() $x_{i}=0$
for all
$x_{i}=0$
for all
![]() $x \in \ker A$
and unfrozen otherwise. Let
$x \in \ker A$
and unfrozen otherwise. Let
![]() $\mathfrak{F}(A)$
be the set of frozen coordinates.
$\mathfrak{F}(A)$
be the set of frozen coordinates.
If
![]() $\mathbb{A}$
had many frozen coordinates then adding an extra random row with three non-zero entries could hardly decrease the nullity w.h.p. For if all three non-zero coordinates fall into the frozen set, then we get the new equation ‘for free’, that is,
$\mathbb{A}$
had many frozen coordinates then adding an extra random row with three non-zero entries could hardly decrease the nullity w.h.p. For if all three non-zero coordinates fall into the frozen set, then we get the new equation ‘for free’, that is,
![]() $\text{nul} \mathbb{A}_{[1]}=\text{nul} \mathbb{A}$
. Thus, Proposition 2.3 implies that
$\text{nul} \mathbb{A}_{[1]}=\text{nul} \mathbb{A}$
. Thus, Proposition 2.3 implies that
![]() $|\mathfrak{F}(\mathbb{A})|=o(n)$
w.h.p. We conclude that
$|\mathfrak{F}(\mathbb{A})|=o(n)$
w.h.p. We conclude that
![]() ${\boldsymbol{x}}_{\mathbb{A},i}$
is uniformly distributed over
${\boldsymbol{x}}_{\mathbb{A},i}$
is uniformly distributed over
![]() $\mathbb{F}_q$
for all but
$\mathbb{F}_q$
for all but
![]() $o(n)$
coordinates
$o(n)$
coordinates
![]() $i\in [n]$
. However, this does not yet imply that
$i\in [n]$
. However, this does not yet imply that
![]() ${\boldsymbol{x}}_{\mathbb{A},i}$
,
${\boldsymbol{x}}_{\mathbb{A},i}$
,
![]() ${\boldsymbol{x}}_{\mathbb{A},j}$
are independent for most
${\boldsymbol{x}}_{\mathbb{A},j}$
are independent for most
![]() $i,j$
, as required by
$i,j$
, as required by
![]() $\mathfrak{O}$
. Yet a more careful argument based on the ‘pinning lemma’ from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] does. The proof of the following statement can be found in Section 5.
$\mathfrak{O}$
. Yet a more careful argument based on the ‘pinning lemma’ from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] does. The proof of the following statement can be found in Section 5.
Proposition 2.4.
Assume that (1.3) is satisfied. Then w.h.p.
![]() $\mathbb{A}\in \mathfrak{O}$
.
$\mathbb{A}\in \mathfrak{O}$
.
2.5 Expansion around the equitable solution
In this part, we consider the more general model
![]() $\underline{\mathbb{A}}$
, that is, the model in Proposition 2.1. As outlined earlier, given that we know (2.8), we can establish (2.9) by expanding (2.5) around the uniform distribution (2.6). At first glance, this may not seem entirely immediate because (2.8) only appears to fix the variables
$\underline{\mathbb{A}}$
, that is, the model in Proposition 2.1. As outlined earlier, given that we know (2.8), we can establish (2.9) by expanding (2.5) around the uniform distribution (2.6). At first glance, this may not seem entirely immediate because (2.8) only appears to fix the variables
![]() $(z_i(\sigma ))_{i,\sigma }$
of (2.5) that correspond to the variable nodes. But thanks to a certain inherent symmetry property the optimal
$(z_i(\sigma ))_{i,\sigma }$
of (2.5) that correspond to the variable nodes. But thanks to a certain inherent symmetry property the optimal
![]() $\hat z_{\chi _1,\ldots,\chi _\ell }$
to go with the check nodes end up being nearly equitable as well. This observation by itself now suffices to show without further ado that
$\hat z_{\chi _1,\ldots,\chi _\ell }$
to go with the check nodes end up being nearly equitable as well. This observation by itself now suffices to show without further ado that
Yet the estimate (2.13) is not quite precise enough to complete the proof of Proposition 2.1. Indeed, to apply Chebyshev’s inequality we would need asymptotic equality as in (2.9) rather than just an
![]() $O(\!\cdot\!)$
-bound; Huang [Reference Huang27] faced the same issue in the case
$O(\!\cdot\!)$
-bound; Huang [Reference Huang27] faced the same issue in the case
![]() ${\boldsymbol{d}}={\boldsymbol{k}}$
constant and
${\boldsymbol{d}}={\boldsymbol{k}}$
constant and
![]() $q$
prime. The proof of this seemingly innocuous improvement actually constitutes one of the main technical obstacles that we need to surmount.
$q$
prime. The proof of this seemingly innocuous improvement actually constitutes one of the main technical obstacles that we need to surmount.
As a first step, using a careful local expansion we will show that the dominant contribution to the second moment actually comes from
![]() $(z_\ell )_\ell$
such that
$(z_\ell )_\ell$
such that
 \begin{align} \sum _{\ell \geq 0} \sum _{i=1}^n \frac{{\mathbb{1}}{\{d_i=\ell \}}}{n} \sum _{\sigma \in \mathbb{F}_q}|z_\ell (\sigma )-q^{-1}|&=O(n^{-1/2}). \end{align}
\begin{align} \sum _{\ell \geq 0} \sum _{i=1}^n \frac{{\mathbb{1}}{\{d_i=\ell \}}}{n} \sum _{\sigma \in \mathbb{F}_q}|z_\ell (\sigma )-q^{-1}|&=O(n^{-1/2}). \end{align}
But even once we know (2.14) a critical issue remains because we allow general distributions of degrees
![]() $d_1, \ldots,$
$d_1, \ldots,$
![]() $d_n$
,
$d_n$
,
![]() $k_1,\ldots,k_m$
and matrix entries
$k_1,\ldots,k_m$
and matrix entries
![]() $\boldsymbol{\chi }$
. In effect, to estimate the kernel size accurately we need to investigate the conceivable frequencies of field values that can lead to solutions. Specifically, for an integer
$\boldsymbol{\chi }$
. In effect, to estimate the kernel size accurately we need to investigate the conceivable frequencies of field values that can lead to solutions. Specifically, for an integer
![]() $k_0\geq 3$
and
$k_0\geq 3$
and
![]() $\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
let
$\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
let
 \begin{equation} \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})=\left \{{\sigma \in \mathbb{F}_q^{k_0}\;:\;\sum _{i=1}^{k_0}\chi _i\sigma _i=0}\right \} \end{equation}
\begin{equation} \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})=\left \{{\sigma \in \mathbb{F}_q^{k_0}\;:\;\sum _{i=1}^{k_0}\chi _i\sigma _i=0}\right \} \end{equation}
comprise all solutions to a linear equation with coefficients
![]() $\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q$
. For each
$\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q$
. For each
![]() $\sigma \in \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})$
the vector
$\sigma \in \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})$
the vector
 \begin{align} \hat{\sigma }=\left ({\sum _{i=1}^{k_0}{\mathbb{1}}\left \{{\sigma _i=s}\right \}}\right )_{s\in \mathbb{F}_q^*}\in \mathbb{Z}^{\mathbb{F}_q^*} \end{align}
\begin{align} \hat{\sigma }=\left ({\sum _{i=1}^{k_0}{\mathbb{1}}\left \{{\sigma _i=s}\right \}}\right )_{s\in \mathbb{F}_q^*}\in \mathbb{Z}^{\mathbb{F}_q^*} \end{align}
tracks the frequencies with which the various non-zero field elements appear. Depending on the coefficients
![]() $\chi _1,\ldots,\chi _{k_0}$
, the frequency vectors
$\chi _1,\ldots,\chi _{k_0}$
, the frequency vectors
![]() $\hat{\sigma }$
may be confined to a proper sub-grid of the integer lattice. For example, in the case
$\hat{\sigma }$
may be confined to a proper sub-grid of the integer lattice. For example, in the case
![]() $q=k_0=3$
and
$q=k_0=3$
and
![]() $\chi _1=\chi _2=\chi _3=1$
they span the sub-lattice spanned by
$\chi _1=\chi _2=\chi _3=1$
they span the sub-lattice spanned by
![]() $\binom 11$
and
$\binom 11$
and
![]() $\binom 03$
. The following proposition characterises the lattice spanned by the frequency vectors for general
$\binom 03$
. The following proposition characterises the lattice spanned by the frequency vectors for general
![]() $k_0$
and
$k_0$
and
![]() $\chi _1,\ldots,\chi _{k_0}$
.
$\chi _1,\ldots,\chi _{k_0}$
.
Proposition 2.5.
Let
![]() $k_0\geq 3$
, let
$k_0\geq 3$
, let
![]() $\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
and let
$\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
and let
![]() $\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})\subseteq \mathbb{Z}^{\mathbb{F}_q^*}$
be the
$\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})\subseteq \mathbb{Z}^{\mathbb{F}_q^*}$
be the
![]() $\mathbb{Z}$
-module generated by the frequency vectors
$\mathbb{Z}$
-module generated by the frequency vectors
![]() $\hat{\sigma }$
for
$\hat{\sigma }$
for
![]() $\sigma \in \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})$
. Then
$\sigma \in \mathcal{S}_q(\chi _1,\ldots,\chi _{k_0})$
. Then
![]() $\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
has a basis
$\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
has a basis
![]() $(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors with
$(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors with
![]() $\|\mathfrak{b}_i\|_1\leq 3$
for all
$\|\mathfrak{b}_i\|_1\leq 3$
for all
![]() $1\leq i\leq q-1$
such that
$1\leq i\leq q-1$
such that
![]() $\text{det}_{\mathbb{Z}}\left ({\mathfrak{b}_1\ \cdots \ \mathfrak{b}_{q-1}}\right )=q^{{\mathbb{1}}\{\chi _1=\cdots =\chi _{k_0}\}}.$
$\text{det}_{\mathbb{Z}}\left ({\mathfrak{b}_1\ \cdots \ \mathfrak{b}_{q-1}}\right )=q^{{\mathbb{1}}\{\chi _1=\cdots =\chi _{k_0}\}}.$
A vital feature of Proposition 2.5 is that the module basis consists of non-negative integer vectors with small
![]() $\ell _1$
-norm. In effect, the basis vectors are ‘combinatorially meaningful’ towards our purpose of counting solutions. Perhaps surprisingly, the proof of Proposition 2.5 turns out to be rather delicate, with details depending on whether
$\ell _1$
-norm. In effect, the basis vectors are ‘combinatorially meaningful’ towards our purpose of counting solutions. Perhaps surprisingly, the proof of Proposition 2.5 turns out to be rather delicate, with details depending on whether
![]() $q$
is a prime or a prime power, among other things. The details can be found in Section 6.
$q$
is a prime or a prime power, among other things. The details can be found in Section 6.
In addition to the sub-grid constraints imposed by the linear equations themselves, we need to take a divisibility condition into account. Indeed, for any assignment
![]() $\sigma \in \mathbb{F}_q^n$
of values to variables, the frequencies of the various field elements
$\sigma \in \mathbb{F}_q^n$
of values to variables, the frequencies of the various field elements
![]() $s\in \mathbb{F}_q$
are divisible by the g.c.d.
$s\in \mathbb{F}_q$
are divisible by the g.c.d.
![]() $\mathfrak{d}$
of
$\mathfrak{d}$
of
![]() $d_1,\ldots,d_n$
, that is,
$d_1,\ldots,d_n$
, that is,
To compute the expected kernel size we need to study the intersection of the sub-grid (2.17) with the grid spanned by the frequency vectors
![]() $\hat{\sigma }$
for
$\hat{\sigma }$
for
![]() $\sigma \in \mathcal{S}_q(\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,k})$
. Specifically, by way of estimating the number of assignments represented by each grid point and calculating the ensuing satisfiability probability, we obtain the following.
$\sigma \in \mathcal{S}_q(\boldsymbol{\chi }_{1,1},\ldots,\boldsymbol{\chi }_{1,k})$
. Specifically, by way of estimating the number of assignments represented by each grid point and calculating the ensuing satisfiability probability, we obtain the following.
Proposition 2.6.
Assume that
![]() $q$
and
$q$
and
![]() $\mathfrak{d}$
are coprime. Then (2.9) holds w.h.p.
$\mathfrak{d}$
are coprime. Then (2.9) holds w.h.p.
We prove Proposition 2.6 in Section 7. Combining Propositions 2.3–2.6, we now establish the main theorems.
Proof of Proposition
2.1. Assumption (1.3) implies that
![]() $1-d/k=\Phi (0)\gt{\Phi (1)={\mathbb{P}}\left ({{\boldsymbol{d}}=0}\right ) \geq 0}$
. Combining (2.11) and Proposition 2.6, we obtain (2.8)–(2.9) for the matrix
$1-d/k=\Phi (0)\gt{\Phi (1)={\mathbb{P}}\left ({{\boldsymbol{d}}=0}\right ) \geq 0}$
. Combining (2.11) and Proposition 2.6, we obtain (2.8)–(2.9) for the matrix
![]() $\underline{\mathbb{A}}$
. Hence, Chebyshev’s inequality and assumption (P5) imply that
$\underline{\mathbb{A}}$
. Hence, Chebyshev’s inequality and assumption (P5) imply that
![]() ${\boldsymbol{Z}}\geq (1-o(1))q^{n-m}$
${\boldsymbol{Z}}\geq (1-o(1))q^{n-m}$
![]() $=q^{n(1-d/k+o(1))}\gt 0$
w.h.p. Consequently, the random linear system
$=q^{n(1-d/k+o(1))}\gt 0$
w.h.p. Consequently, the random linear system
![]() $\underline{\mathbb{A}} x={\boldsymbol{y}}$
has a solution w.h.p., and thus
$\underline{\mathbb{A}} x={\boldsymbol{y}}$
has a solution w.h.p., and thus
![]() ${\text{rk}}\underline{\mathbb{A}}=m$
w.h.p.
${\text{rk}}\underline{\mathbb{A}}=m$
w.h.p.
Proof of Corollary
1.2. Let
![]() $q$
be a prime that does not divide
$q$
be a prime that does not divide
![]() $\mathfrak{d}$
and let
$\mathfrak{d}$
and let
![]() $\boldsymbol{\chi }=1$
deterministically. Obtain the matrix
$\boldsymbol{\chi }=1$
deterministically. Obtain the matrix
![]() $\bar{\mathbb{B}}\in \mathbb{F}_q^{{\boldsymbol{m}}\times n}$
by reading the
$\bar{\mathbb{B}}\in \mathbb{F}_q^{{\boldsymbol{m}}\times n}$
by reading the
![]() $\{0,1\}$
-entries of
$\{0,1\}$
-entries of
![]() $\mathbb{B}$
as elements of
$\mathbb{B}$
as elements of
![]() $\mathbb{F}_q$
. Then the distribution of
$\mathbb{F}_q$
. Then the distribution of
![]() $\bar{\mathbb{B}}$
coincides with the distribution of the random
$\bar{\mathbb{B}}$
coincides with the distribution of the random
![]() $\mathbb{F}_q$
-matrix
$\mathbb{F}_q$
-matrix
![]() $\mathbb{A}$
. Hence, Theorem 1.1 implies that
$\mathbb{A}$
. Hence, Theorem 1.1 implies that
![]() $\bar{\mathbb{B}}$
has full row rank w.h.p.
$\bar{\mathbb{B}}$
has full row rank w.h.p.
Suppose that indeed
![]() ${\text{rk}}\bar{\mathbb{B}}={\boldsymbol{m}}$
. We claim that then the rows of
${\text{rk}}\bar{\mathbb{B}}={\boldsymbol{m}}$
. We claim that then the rows of
![]() $\mathbb{B}$
are linearly independent. Indeed, assume that
$\mathbb{B}$
are linearly independent. Indeed, assume that
![]() $z^\top \mathbb{B}=0$
for some vector
$z^\top \mathbb{B}=0$
for some vector
![]() $z=(z_1,\ldots,z_{{\boldsymbol{m}}})^\top \in \mathbb{Z}^{{\boldsymbol{m}}}$
. Factoring out
$z=(z_1,\ldots,z_{{\boldsymbol{m}}})^\top \in \mathbb{Z}^{{\boldsymbol{m}}}$
. Factoring out
![]() $\gcd (z_1,\ldots,z_{{\boldsymbol{m}}})$
if necessary, we may assume that the vector
$\gcd (z_1,\ldots,z_{{\boldsymbol{m}}})$
if necessary, we may assume that the vector
![]() $\bar z\in \mathbb{F}_q^{{\boldsymbol{m}}}$
with entries
$\bar z\in \mathbb{F}_q^{{\boldsymbol{m}}}$
with entries
![]() $\bar z_i=z_i+q\mathbb{Z}$
is non-zero. Since
$\bar z_i=z_i+q\mathbb{Z}$
is non-zero. Since
![]() $z^\top \mathbb{B}=0$
implies that
$z^\top \mathbb{B}=0$
implies that
![]() $\bar z^\top \bar{\mathbb{B}}=0$
, the rows of
$\bar z^\top \bar{\mathbb{B}}=0$
, the rows of
![]() $\bar{\mathbb{B}}$
are linearly dependent, in contradiction to our assumption that
$\bar{\mathbb{B}}$
are linearly dependent, in contradiction to our assumption that
![]() $\bar{\mathbb{B}}$
has full row rank.
$\bar{\mathbb{B}}$
has full row rank.
2.6 Discussion and related work
The present proof strategy draws on the prior work [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] on the rank of random matrices. Specifically, toward the proof of Proposition 2.3 we extend the Aizenman-Sims-Starr technique from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] and to prove Proposition 2.4 we generalise an argument from [Reference Ayre, Coja-Oghlan, Gao and Müller6]. Additionally, the expansion around the centre carried out in the proof of Proposition 2.6 employs some of the techniques developed in the study of satisfiability thresholds, particularly the extensive use of local limit theorems and auxiliary probability spaces [Reference Coja-Oghlan12, Reference Coja-Oghlan13].
The principal new proof ingredient is the asymptotically precise analysis of the second moment by means of the study of the sub-grids of the integer lattice induced by the constraints as sketched in Section 2.5. This issue was absent in the prior literature on variations on random
![]() $k$
-XORSAT [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Reference Cooper, Frieze and Pegden15] and on other random constraint satisfaction problems [Reference Coja-Oghlan12, Reference Coja-Oghlan13]. However, in the study of the random regular matrix from Example 1.5 Huang [Reference Huang27] faced a similar issue in the special case
$k$
-XORSAT [Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Reference Cooper, Frieze and Pegden15] and on other random constraint satisfaction problems [Reference Coja-Oghlan12, Reference Coja-Oghlan13]. However, in the study of the random regular matrix from Example 1.5 Huang [Reference Huang27] faced a similar issue in the special case
![]() ${\boldsymbol{d}}={\boldsymbol{k}}$
constant and
${\boldsymbol{d}}={\boldsymbol{k}}$
constant and
![]() $\boldsymbol{\chi }=1$
deterministically. Proposition 2.5, whose proof is based on a combinatorial investigation of lattices in the general case, constitutes a generalisation of the case Huang studied. A further feature of Proposition 2.5 absent in ref. [Reference Huang27] is the explicit
$\boldsymbol{\chi }=1$
deterministically. Proposition 2.5, whose proof is based on a combinatorial investigation of lattices in the general case, constitutes a generalisation of the case Huang studied. A further feature of Proposition 2.5 absent in ref. [Reference Huang27] is the explicit
![]() $\ell _1$
-bound on the basis vectors. This bound facilitates the proof of Proposition 2.6, which ultimately carries out the expansion around the equitable solution.
$\ell _1$
-bound on the basis vectors. This bound facilitates the proof of Proposition 2.6, which ultimately carries out the expansion around the equitable solution.
Satisfiability thresholds of random constraint satisfaction problems have been studied extensively in the statistical physics literature via a non-rigorous technique called the ‘cavity method’. The cavity method comes in two installments: the simpler ‘replica symmetric ansatz’ associated with the Belief Propagation message passing scheme, and the more intricate ‘replica symmetry breaking ansatz’. The proof of Theorem 1.1 demonstrates that the former renders the correct prediction as to the satisfiability threshold of random linear equations. By contrast, in quite a few problems, notoriously random
![]() $k$
-SAT, replica symmetry breaking occurs [Reference Coja-Oghlan, Müller and Ravelomanana14, Reference Ding and Sly20].
$k$
-SAT, replica symmetry breaking occurs [Reference Coja-Oghlan, Müller and Ravelomanana14, Reference Ding and Sly20].
An intriguing question for future work might be to understand the ‘critical’ case of
![]() $\Phi$
that attain their global max at
$\Phi$
that attain their global max at
![]() $0$
and another point left open by Theorem 1.1. While Example 1.4 shows that it cannot generally be true that
$0$
and another point left open by Theorem 1.1. While Example 1.4 shows that it cannot generally be true that
![]() $\mathbb{A}$
has full row rank w.h.p., the regular case where
$\mathbb{A}$
has full row rank w.h.p., the regular case where
![]() ${\boldsymbol{d}}={\boldsymbol{k}}=d$
are fixed to the same constant provides an intriguing example. For this scenario Huang proved that the random
${\boldsymbol{d}}={\boldsymbol{k}}=d$
are fixed to the same constant provides an intriguing example. For this scenario Huang proved that the random
![]() $\{0,1\}$
-matrix
$\{0,1\}$
-matrix
![]() $\mathbb{B}$
has full rank w.h.p. [Reference Huang27]. The proof, based effectively on a moment computation over finite fields and local limit techniques, also applies to the adjacency matrices of random
$\mathbb{B}$
has full rank w.h.p. [Reference Huang27]. The proof, based effectively on a moment computation over finite fields and local limit techniques, also applies to the adjacency matrices of random
![]() $d$
-regular graphs.
$d$
-regular graphs.
While the present paper deals with sparse random matrices with a bounded average number of non-zero entries in each row and column, the case of dense random matrices has received a great deal of attention, too. Komlós [Reference Komlós34] first shows that dense square random
![]() $\{0,1\}$
-matrices are regular over the rationals w.h.p.; Vu [Reference Vu50] suggested an alternative proof. The computation of the exponential order of the singularity probability subsequently led to a series of intriguing articles [Reference Kahn, Komloś and Szemerédi30, Reference Tao and Vu48, Reference Tikhomirov49]. By contrast, the singularity probability of a dense square matrix over a finite field converges to a value strictly between zero and one [Reference Kovalenko35, Reference Kovalenko, Levitskaya and Savchuk36, Reference Levitskaya38, Reference Levitskaya39].
$\{0,1\}$
-matrices are regular over the rationals w.h.p.; Vu [Reference Vu50] suggested an alternative proof. The computation of the exponential order of the singularity probability subsequently led to a series of intriguing articles [Reference Kahn, Komloś and Szemerédi30, Reference Tao and Vu48, Reference Tikhomirov49]. By contrast, the singularity probability of a dense square matrix over a finite field converges to a value strictly between zero and one [Reference Kovalenko35, Reference Kovalenko, Levitskaya and Savchuk36, Reference Levitskaya38, Reference Levitskaya39].
Apart from the sparse and dense case, the regime of intermediate densities has been studied as well. Balakin [Reference Balakin7] and Blömer, Karp and Welzl [Reference Blömer, Karp and Welzl8] dealt with the rank of such random matrices of intermediate densities over finite fields. In addition, Costello and Vu [Reference Costello16, Reference Costello and Vu17] studied the rational rank of random symmetric matrices of an intermediate density.
Indeed, an interesting open problem appears to be the extension of the present methods to the symmetric case. In particular, it would be interesting to see if the present techniques can be used to add to the line of works on the adjacency matrices of random graphs, which have been approached by means of techniques based on local weak convergence or Littlewood-Offord techniques [Reference Bordenave, Lelarge and Salez9, Reference Ferber, Kwan, Sah and Sawhney22]. Several core ideas of [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] have recently been used to study the asymptotic rank of a special class of symmetric random matrices [Reference van der Hofstad, Müller and Zhu26].
2.7 Organisation
After some preliminaries in Section 3 we begin with the proof of Proposition 2.3 in Section 4. The proof relies on an Aizenman-Sims-Starr coupling argument, some details of which are deferred to Section 8. Section 5 deals with the proof of Proposition 2.4. Subsequently we prove Proposition 2.5 in Section 6, thereby laying the ground for the proof of Proposition 2.6 in Section 7.
3. Preliminaries
Unsurprisingly, the proofs of the main results involve a few concepts and ideas from linear algebra. We mostly follow the terminology from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10], summarised in the following definition.
Definition 3.1 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Definition 2.1]). Let
![]() $A$
be an
$A$
be an
![]() $m\times n$
-matrix over a field
$m\times n$
-matrix over a field
![]() $\mathbb{F}$
.
$\mathbb{F}$
.
-
• A set
 $\emptyset \neq I\subseteq [n]$
is a
relation
of
$\emptyset \neq I\subseteq [n]$
is a
relation
of
 $A$
if there exists a row vector
$A$
if there exists a row vector
 $y\in \mathbb{F}^{1\times m}$
such that
$y\in \mathbb{F}^{1\times m}$
such that
 $\emptyset \neq{\text{supp}}(y A)\subseteq I$
.
$\emptyset \neq{\text{supp}}(y A)\subseteq I$
. -
• If
 $I=\left \{{i}\right \}$
is a relation of
$I=\left \{{i}\right \}$
is a relation of
 $A$
, then we call
$A$
, then we call
 $i$
frozen
in
$i$
frozen
in
 $A$
. Let
$A$
. Let
 $\mathfrak{F}(A)$
be the set of all frozen
$\mathfrak{F}(A)$
be the set of all frozen
 $i\in [n]$
and let
$i\in [n]$
and let
 \begin{equation*}\mathfrak {f}(A)=|\mathfrak {F}(A)|/n.\end{equation*}
\begin{equation*}\mathfrak {f}(A)=|\mathfrak {F}(A)|/n.\end{equation*}
-
• A set
 $I\subseteq [n]$
is a
proper relation
of
$I\subseteq [n]$
is a
proper relation
of
 $A$
if
$A$
if
 $I\setminus \mathfrak{F}(A)$
is a relation of
$I\setminus \mathfrak{F}(A)$
is a relation of
 $A$
.
$A$
. -
• For
 $\delta \gt 0$
,
$\delta \gt 0$
,
 $\ell \geq 1$
we say that
$\ell \geq 1$
we say that
 $A$
is
$A$
is
 $\boldsymbol{(\delta,\ell )}$
-
free
if there are no more than
$\boldsymbol{(\delta,\ell )}$
-
free
if there are no more than
 $\delta n^\ell$
proper relations
$\delta n^\ell$
proper relations
 $I\subseteq [n]$
of size
$I\subseteq [n]$
of size
 $|I|=\ell$
.
$|I|=\ell$
.
Thus, a relation is set of column indices such that the support of a non-zero linear combination
![]() $yA$
of rows of
$yA$
of rows of
![]() $A$
is contained in that set of indices. Of course, every single row induces a relation on the column indices where it has non-zero entries. An important special case is a relation consisting of one coordinate
$A$
is contained in that set of indices. Of course, every single row induces a relation on the column indices where it has non-zero entries. An important special case is a relation consisting of one coordinate
![]() $i$
only. If such a relation exists, then
$i$
only. If such a relation exists, then
![]() $x_i=0$
for all vectors
$x_i=0$
for all vectors
![]() $x\in \ker A$
, which is why we call such a coordinate
$x\in \ker A$
, which is why we call such a coordinate
![]() $i$
frozen. Furthermore, a proper relation is a relation that is not just built up of frozen variables. Finally, we introduce the term
$i$
frozen. Furthermore, a proper relation is a relation that is not just built up of frozen variables. Finally, we introduce the term
![]() $(\delta,\ell )$
-free to express that
$(\delta,\ell )$
-free to express that
![]() $A$
has ‘relatively few’ relations of size
$A$
has ‘relatively few’ relations of size
![]() $\ell$
as we will generally employ this term for bounded
$\ell$
as we will generally employ this term for bounded
![]() $\ell$
and small
$\ell$
and small
![]() $\delta \gt 0$
.
$\delta \gt 0$
.
The following observation will aid the Aizenman-Sims-Starr coupling argument, where we will need to study the effect of adding a few extra rows and columns to a random matrix.
Lemma 3.2 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 2.5]). Let
![]() $A,B,C$
be matrices of size
$A,B,C$
be matrices of size
![]() $m \times n$
,
$m \times n$
,
![]() $m'\times n$
and
$m'\times n$
and
![]() $m'\times n'$
, respectively, and let
$m'\times n'$
, respectively, and let
![]() $I\subseteq [n]$
be the set of all indices of non-zero columns of
$I\subseteq [n]$
be the set of all indices of non-zero columns of
![]() $B$
. Moreover, obtain
$B$
. Moreover, obtain
![]() $B_*$
from
$B_*$
from
![]() $B$
by replacing for each
$B$
by replacing for each
![]() $i\in I\cap \mathfrak{F}(A)$
the
$i\in I\cap \mathfrak{F}(A)$
the
![]() $i$
-th column of
$i$
-th column of
![]() $B$
by zero. Unless
$B$
by zero. Unless
![]() $I$
is a proper relation of
$I$
is a proper relation of
![]() $A$
we have
$A$
we have
 \begin{align} \text{nul}\begin{pmatrix}A&0\\[5pt] B&C\end{pmatrix}-\text{nul}\; A=n'-{\text{rk}}(B_*\ C). \end{align}
\begin{align} \text{nul}\begin{pmatrix}A&0\\[5pt] B&C\end{pmatrix}-\text{nul}\; A=n'-{\text{rk}}(B_*\ C). \end{align}
Apart from Lemma 3.2 we will harness an important trick called the ‘pinning operation’. The key insight is that for any given matrix we can diminish the number of short proper relations by simply expressly freezing a few random coordinates. The basic idea behind the pinning operation goes back to the work of Montanari [Reference Montanari43] and has been used in other contexts [Reference Coja-Oghlan, Krzakala, Perkins and Zdeborova11, Reference Raghavendra46]. The version of the construction that we use here goes as follows.
Definition 3.3 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Definition 2.3]). Let
![]() $A$
be an
$A$
be an
![]() $m\times n$
matrix and let
$m\times n$
matrix and let
![]() $\theta \geq 0$
be an integer. Let
$\theta \geq 0$
be an integer. Let
![]() ${\boldsymbol{i}}_1,{\boldsymbol{i}}_2,\ldots,{\boldsymbol{i}}_\theta \in [n]$
be uniformly random and mutually independent column indices. Then the matrix
${\boldsymbol{i}}_1,{\boldsymbol{i}}_2,\ldots,{\boldsymbol{i}}_\theta \in [n]$
be uniformly random and mutually independent column indices. Then the matrix
![]() $A[\theta ]$
is obtained by adding
$A[\theta ]$
is obtained by adding
![]() $\theta$
new rows to
$\theta$
new rows to
![]() $A$
such that for each
$A$
such that for each
![]() $j\in [\theta ]$
the
$j\in [\theta ]$
the
![]() $j$
-th new row has precisely one non-zero entry, namely a one in the
$j$
-th new row has precisely one non-zero entry, namely a one in the
![]() ${\boldsymbol{i}}_j$
-th column.
${\boldsymbol{i}}_j$
-th column.
Proposition 3.4 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proposition 2.4]). For any
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
![]() $\ell \gt 0$
there exists
$\ell \gt 0$
there exists
![]() $\Theta _0=\Theta _0(\delta,\ell )\gt 0$
such that for all
$\Theta _0=\Theta _0(\delta,\ell )\gt 0$
such that for all
![]() $\Theta \gt \Theta _0$
and for any matrix
$\Theta \gt \Theta _0$
and for any matrix
![]() $A$
over any field
$A$
over any field
![]() $\mathbb{F}$
the following is true. With
$\mathbb{F}$
the following is true. With
![]() $\boldsymbol{\theta }\in [\Theta ]$
chosen uniformly at random we have
$\boldsymbol{\theta }\in [\Theta ]$
chosen uniformly at random we have
![]() ${\mathbb{P}}\left \lbrack{\mbox{$A[\boldsymbol{\theta }]$ is $(\delta,\ell )$-free}}\right \rbrack \gt 1-\delta .$
${\mathbb{P}}\left \lbrack{\mbox{$A[\boldsymbol{\theta }]$ is $(\delta,\ell )$-free}}\right \rbrack \gt 1-\delta .$
At first sight, it might appear surprising that Proposition 3.4 does not depend on the matrix
![]() $A$
at all. It is here where the randomness in the number of added unit rows
$A$
at all. It is here where the randomness in the number of added unit rows
![]() $\boldsymbol{\theta }$
comes into play: On a heuristic level, the proof of Proposition 3.4 is based on tracing the effect of adding unit rows over a sufficiently large number of steps. Throughout this process, irrespective of the underlying matrix
$\boldsymbol{\theta }$
comes into play: On a heuristic level, the proof of Proposition 3.4 is based on tracing the effect of adding unit rows over a sufficiently large number of steps. Throughout this process, irrespective of the underlying matrix
![]() $A$
, there cannot be too many steps where the expected increase in the size of the set of frozen variables is large, since their number is trivially bounded above by
$A$
, there cannot be too many steps where the expected increase in the size of the set of frozen variables is large, since their number is trivially bounded above by
![]() $n$
. Thus, when choosing a uniformly random number of unit rows to append, we have to be truly unlucky to hit exactly one of these few steps. On the other hand, a multitude of proper linear relations at any given point increases the chances to freeze a large number of variables upon addition of one more unit row, and therefore there also cannot be too many such moments throughout the process of adding unit rows. Of course, the precise details of the proof are more involved, and we refer the interested reader to [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10].
$n$
. Thus, when choosing a uniformly random number of unit rows to append, we have to be truly unlucky to hit exactly one of these few steps. On the other hand, a multitude of proper linear relations at any given point increases the chances to freeze a large number of variables upon addition of one more unit row, and therefore there also cannot be too many such moments throughout the process of adding unit rows. Of course, the precise details of the proof are more involved, and we refer the interested reader to [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10].
As a fairly immediate application of Proposition 3.4 we conclude that if the pinning operation applied to a random matrix over a finite field leaves us with few frozen variables, a decorrelation condition akin to the event
![]() $\mathfrak{O}$
from (2.7) will be satisfied. For a matrix
$\mathfrak{O}$
from (2.7) will be satisfied. For a matrix
![]() $A$
we continue to denote by
$A$
we continue to denote by
![]() ${\boldsymbol{x}}_A$
a uniformly random vector from
${\boldsymbol{x}}_A$
a uniformly random vector from
![]() $\ker A$
.
$\ker A$
.
Corollary 3.5 ([Reference Ayre, Coja-Oghlan, Gao and Müller6, Lemma 4.2]). For any
![]() $\zeta \gt 0$
and any prime power
$\zeta \gt 0$
and any prime power
![]() $q\gt 0$
there exist
$q\gt 0$
there exist
![]() $\xi \gt 0$
and
$\xi \gt 0$
and
![]() $\Theta _0\gt 0$
such that for any
$\Theta _0\gt 0$
such that for any
![]() $\Theta \gt \Theta _0$
for large enough
$\Theta \gt \Theta _0$
for large enough
![]() $n$
the following is true. Let
$n$
the following is true. Let
![]() $A$
be a
$A$
be a
![]() $m\times n$
-matrix over
$m\times n$
-matrix over
![]() $\mathbb{F}_q$
. Suppose that for a uniformly random
$\mathbb{F}_q$
. Suppose that for a uniformly random
![]() $\boldsymbol{\theta }\in [\Theta ]$
we have
$\boldsymbol{\theta }\in [\Theta ]$
we have
![]() $\mathbb{E}|\mathfrak{F}(A[\boldsymbol{\theta }])|\lt \xi n$
. Then
$\mathbb{E}|\mathfrak{F}(A[\boldsymbol{\theta }])|\lt \xi n$
. Then
 \begin{equation*}\sum _{\sigma,\tau \in \mathbb {F}_q}\sum _{i,j=1}^n\mathbb {E}\left |{{\mathbb {P}}\left \lbrack {\boldsymbol {x}_i=\sigma,\,\boldsymbol {x}_j=\tau \mid {A}}\right \rbrack -q^{-2}}\right |\lt \zeta n^2.\end{equation*}
\begin{equation*}\sum _{\sigma,\tau \in \mathbb {F}_q}\sum _{i,j=1}^n\mathbb {E}\left |{{\mathbb {P}}\left \lbrack {\boldsymbol {x}_i=\sigma,\,\boldsymbol {x}_j=\tau \mid {A}}\right \rbrack -q^{-2}}\right |\lt \zeta n^2.\end{equation*}
As mentioned earlier, at a key junction of the moment computation we will need to estimate the number of integer lattice points that satisfy certain linear relations. The following elementary estimate will prove useful.
Lemma 3.6. [Reference Lenstra, Buhler and Stevenhagen37, p. 135] Let
![]() $\mathfrak{M}\subseteq{\mathbb{R}}^\ell$
be a
$\mathfrak{M}\subseteq{\mathbb{R}}^\ell$
be a
![]() $\mathbb{Z}$
-module with basis
$\mathbb{Z}$
-module with basis
![]() $b_1,\ldots,b_\ell$
. Then
$b_1,\ldots,b_\ell$
. Then
The definition of the random Tanner graph in Section 1.2.1 provides that
![]() $\mathbb{G}$
is simple. Commonly it is easier to conduct proofs for an auxiliary random multi-graph drawn from a pairing model and then lift the results to the simple random graph. This is how we proceed as well. Given (1.1) we let
$\mathbb{G}$
is simple. Commonly it is easier to conduct proofs for an auxiliary random multi-graph drawn from a pairing model and then lift the results to the simple random graph. This is how we proceed as well. Given (1.1) we let
![]() ${\boldsymbol{G}}$
be the random bipartite graph on the set
${\boldsymbol{G}}$
be the random bipartite graph on the set
![]() $\{x_1,\ldots,x_n\}$
of variable nodes and
$\{x_1,\ldots,x_n\}$
of variable nodes and
![]() $\{a_1,\ldots,a_{{\boldsymbol{m}}}\}$
of check nodes generated by drawing a perfect matching
$\{a_1,\ldots,a_{{\boldsymbol{m}}}\}$
of check nodes generated by drawing a perfect matching
![]() $\boldsymbol{\Gamma }$
of the complete bipartite graph on
$\boldsymbol{\Gamma }$
of the complete bipartite graph on
 \begin{equation*}\bigcup _{i=1}^n\left \{{x_i}\right \}\times [\textbf {d}_i]\qquad \mbox {and}\qquad \bigcup _{i=1}^{\textbf {m}}\left \{{a_i}\right \}\times [\boldsymbol {k_i}]\end{equation*}
\begin{equation*}\bigcup _{i=1}^n\left \{{x_i}\right \}\times [\textbf {d}_i]\qquad \mbox {and}\qquad \bigcup _{i=1}^{\textbf {m}}\left \{{a_i}\right \}\times [\boldsymbol {k_i}]\end{equation*}
and contracting the sets
![]() $x_i\times [\textbf{d}_i]$
and
$x_i\times [\textbf{d}_i]$
and
![]() $a_i\times [{\boldsymbol{k}}_{\boldsymbol{i}}]$
of variable/check clones. We also let
$a_i\times [{\boldsymbol{k}}_{\boldsymbol{i}}]$
of variable/check clones. We also let
![]() ${\boldsymbol{A}}$
be the random matrix to go with this random multi-graph. Hence,
${\boldsymbol{A}}$
be the random matrix to go with this random multi-graph. Hence,
 \begin{equation*}\boldsymbol{A}_{ij}=\boldsymbol {\chi }_{i,j}\sum _{u=1}^{\boldsymbol {k_i}}\sum _{v=1}^{\textbf {d}_j}{\mathbb{1}}\{\{(a_i,u),(x_j,v)\}\in \boldsymbol {\Gamma }\}.\end{equation*}
\begin{equation*}\boldsymbol{A}_{ij}=\boldsymbol {\chi }_{i,j}\sum _{u=1}^{\boldsymbol {k_i}}\sum _{v=1}^{\textbf {d}_j}{\mathbb{1}}\{\{(a_i,u),(x_j,v)\}\in \boldsymbol {\Gamma }\}.\end{equation*}
Similarly, given fixed-degree sequences
![]() $(d_1,\ldots,d_n)$
and
$(d_1,\ldots,d_n)$
and
![]() $(k_1,\ldots, k_m)$
with
$(k_1,\ldots, k_m)$
with
![]() $\sum _{i=1}^nd_i = \sum _{j=1}^m k_j$
, we may define a random bipartite graph
$\sum _{i=1}^nd_i = \sum _{j=1}^m k_j$
, we may define a random bipartite graph
![]() $\underline{{\boldsymbol{G}}}$
and the corresponding matrix
$\underline{{\boldsymbol{G}}}$
and the corresponding matrix
![]() $\underline{\boldsymbol{A}}$
. The deviating notation only emphasises that the underlying degrees have been fixed in contrast to the i.i.d. model. Moreover, if the degree sequences
$\underline{\boldsymbol{A}}$
. The deviating notation only emphasises that the underlying degrees have been fixed in contrast to the i.i.d. model. Moreover, if the degree sequences
![]() $(d_1,\ldots,d_n)$
and
$(d_1,\ldots,d_n)$
and
![]() $(k_1,\ldots, k_m)$
satisfy (P3), then routine arguments (e.g. see [Reference Janson29]) show that
$(k_1,\ldots, k_m)$
satisfy (P3), then routine arguments (e.g. see [Reference Janson29]) show that
![]() $\underline{{\boldsymbol{G}}}$
is simple with non-vanishing probability.
$\underline{{\boldsymbol{G}}}$
is simple with non-vanishing probability.
Proposition 3.7 ([Reference van der Hofstad25, Theorem 7.12]). Suppose that the degree sequences
![]() $(d_1,\ldots,d_n)$
and
$(d_1,\ldots,d_n)$
and
![]() $(k_1,\ldots, k_m)$
satisfy (P3). Then,
$(k_1,\ldots, k_m)$
satisfy (P3). Then,
![]() ${\mathbb{P}}\left \lbrack{\underline{{\boldsymbol{G}}}\mbox{ is simple}}\right \rbrack =\Omega (1)$
.
${\mathbb{P}}\left \lbrack{\underline{{\boldsymbol{G}}}\mbox{ is simple}}\right \rbrack =\Omega (1)$
.
If
![]() $({\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n)$
and
$({\boldsymbol{d}}_1,\ldots,{\boldsymbol{d}}_n)$
and
![]() $({\boldsymbol{k}}_1,\ldots, {\boldsymbol{k}}_{{\boldsymbol{m}}})$
are i.i.d. copies of
$({\boldsymbol{k}}_1,\ldots, {\boldsymbol{k}}_{{\boldsymbol{m}}})$
are i.i.d. copies of
![]() ${\boldsymbol{d}}$
and
${\boldsymbol{d}}$
and
![]() ${\boldsymbol{k}}$
with
${\boldsymbol{k}}$
with
![]() $\mathbb{E}[{\boldsymbol{d}}^{2}] + \mathbb{E}\left \lbrack{{\boldsymbol{k}}^{2}}\right \rbrack \lt \infty$
as in Section 1.2.1, then a standard Azuma-Hoeffding argument shows that w.h.p. they satisfy (P3).
$\mathbb{E}[{\boldsymbol{d}}^{2}] + \mathbb{E}\left \lbrack{{\boldsymbol{k}}^{2}}\right \rbrack \lt \infty$
as in Section 1.2.1, then a standard Azuma-Hoeffding argument shows that w.h.p. they satisfy (P3).
Corollary 3.8 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 4.3]).
![]() ${\mathbb{P}}\left \lbrack{{\boldsymbol{G}}\mbox{ is simple} \mid \sum _{i=1}^n{\boldsymbol{d}}_i=\sum _{i=1}^{{\boldsymbol{m}}}{\boldsymbol{k}}_i}\right \rbrack =\Omega (1)$
.
${\mathbb{P}}\left \lbrack{{\boldsymbol{G}}\mbox{ is simple} \mid \sum _{i=1}^n{\boldsymbol{d}}_i=\sum _{i=1}^{{\boldsymbol{m}}}{\boldsymbol{k}}_i}\right \rbrack =\Omega (1)$
.
When working with the random graphs
![]() $\mathbb{G}$
or
$\mathbb{G}$
or
![]() ${\boldsymbol{G}}$
we occasionally encounter the size-biased versions
${\boldsymbol{G}}$
we occasionally encounter the size-biased versions
![]() $\hat{{\boldsymbol{d}}},\hat{{\boldsymbol{k}}}$
of the degree distributions defined by
$\hat{{\boldsymbol{d}}},\hat{{\boldsymbol{k}}}$
of the degree distributions defined by
In particular, these distributions occur in the Aizenman-Sims-Starr coupling argument. In that context we will also need the following crude but simple tail bound.
Lemma 3.9 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 1.11]). Let
![]() $(\boldsymbol{\lambda }_i)_{i\geq 1}$
be a sequence of independent copies of an integer-valued random variable
$(\boldsymbol{\lambda }_i)_{i\geq 1}$
be a sequence of independent copies of an integer-valued random variable
![]() $\boldsymbol{\lambda }\geq 0$
with
$\boldsymbol{\lambda }\geq 0$
with
![]() $\mathbb{E}\left \lbrack{\boldsymbol{\lambda }^r}\right \rbrack \lt \infty$
for some
$\mathbb{E}\left \lbrack{\boldsymbol{\lambda }^r}\right \rbrack \lt \infty$
for some
![]() $r\gt 2$
. Further, let
$r\gt 2$
. Further, let
![]() $s$
be a sequence such that
$s$
be a sequence such that
![]() $s=\Theta (n)$
. Then for all
$s=\Theta (n)$
. Then for all
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
 \begin{equation*}{\mathbb {P}}\left \lbrack {\left |{\sum _{i=1}^s (\boldsymbol {\lambda }_i - \mathbb {E}\left \lbrack {\boldsymbol {\lambda }}\right \rbrack )}\right |\gt \delta n}\right \rbrack = o(1/n).\end{equation*}
\begin{equation*}{\mathbb {P}}\left \lbrack {\left |{\sum _{i=1}^s (\boldsymbol {\lambda }_i - \mathbb {E}\left \lbrack {\boldsymbol {\lambda }}\right \rbrack )}\right |\gt \delta n}\right \rbrack = o(1/n).\end{equation*}
Finally, throughout the article we use the common
![]() $O(\!\cdot\!)$
-notation to refer to the limit
$O(\!\cdot\!)$
-notation to refer to the limit
![]() $n\to \infty$
. In addition, we will sometimes need to deal with another parameter
$n\to \infty$
. In addition, we will sometimes need to deal with another parameter
![]() $\varepsilon \gt 0$
. In such cases we use
$\varepsilon \gt 0$
. In such cases we use
![]() $O_\varepsilon (\!\cdot\!)$
and similar symbols to refer to the double limit
$O_\varepsilon (\!\cdot\!)$
and similar symbols to refer to the double limit
![]() $\varepsilon \to 0$
after
$\varepsilon \to 0$
after
![]() $n\to \infty$
.
$n\to \infty$
.
4. Proof of Proposition 2.3
4.1 Overview
The first ingredient of the proof of Proposition 2.3 is a coupling argument inspired by the Aizenman-Sims-Starr scheme from mathematical physics [Reference Aizenman, Sims and Starr5], which also constituted the main ingredient of the proof of the approximate rank formula (1.4) from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. Indeed, the coupling argument here is quite similar to that from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10], with some extra bells and whistles to accommodate the additional ternary equations. We therefore defer that part of the proof to Section 8. The Aizenman-Sims-Starr argument leaves us with a variational formula for a lower bound on the rank of
![]() $\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
. The second proof ingredient is to solve this variational problem. Harnessing the assumption (1.3), we will obtain the explicit expression for the rank provided by Proposition 2.3.
$\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
. The second proof ingredient is to solve this variational problem. Harnessing the assumption (1.3), we will obtain the explicit expression for the rank provided by Proposition 2.3.
Let us come to the details. As explained in Section 3, we will have an easier time working with the pairing model versions
![]() ${\boldsymbol{G}},{\boldsymbol{A}}$
of the Tanner graph and the random matrix. Moreover, to facilitate the coupling argument we will need to poke a few holes, known as ‘cavities’ in physics jargon, into the random matrix. More precisely, we will slightly reduce the number of check nodes and tolerate a small number of variable nodes
${\boldsymbol{G}},{\boldsymbol{A}}$
of the Tanner graph and the random matrix. Moreover, to facilitate the coupling argument we will need to poke a few holes, known as ‘cavities’ in physics jargon, into the random matrix. More precisely, we will slightly reduce the number of check nodes and tolerate a small number of variable nodes
![]() $x_i$
of degree less than
$x_i$
of degree less than
![]() ${\boldsymbol{d}}_i$
. The cavities will provide the flexibility needed to set up the coupling argument. Finally, to be able to assume that the matrices we are dealing with are
${\boldsymbol{d}}_i$
. The cavities will provide the flexibility needed to set up the coupling argument. Finally, to be able to assume that the matrices we are dealing with are
![]() $(\delta,\ell )$
-free with probability close to one, we also add a random, but bounded number of unary checks
$(\delta,\ell )$
-free with probability close to one, we also add a random, but bounded number of unary checks
![]() $p_1, \ldots, p_{\boldsymbol{\theta }}$
, as described in Proposition 3.4. While this measure does not affect the asymptotic rank, quite crucially, it enables our bound on the rank difference in the coupling argument of Section 8.
$p_1, \ldots, p_{\boldsymbol{\theta }}$
, as described in Proposition 3.4. While this measure does not affect the asymptotic rank, quite crucially, it enables our bound on the rank difference in the coupling argument of Section 8.
Formally, let
![]() $\varepsilon, \delta \in (0,1)$
and let
$\varepsilon, \delta \in (0,1)$
and let
![]() $\Theta \geq 0$
be an integer. Ultimately
$\Theta \geq 0$
be an integer. Ultimately
![]() $\Theta$
will depend on
$\Theta$
will depend on
![]() $\varepsilon$
but not on
$\varepsilon$
but not on
![]() $n$
or
$n$
or
![]() $\delta$
. We then construct the random matrix
$\delta$
. We then construct the random matrix
![]() ${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
as follows. Let
${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
as follows. Let
The Tanner multi-graph
![]() $\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
has variable nodes
$\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
has variable nodes
![]() $x_1, \ldots, x_n$
and check nodes
$x_1, \ldots, x_n$
and check nodes
![]() $a_1, \ldots, a_{{\boldsymbol{m}}_{\varepsilon }}, t_1, \ldots, t_{{\boldsymbol{m}}_\delta }, p_1, \ldots, p_{\boldsymbol{\theta }}$
. To connect them draw a random maximum matching
$a_1, \ldots, a_{{\boldsymbol{m}}_{\varepsilon }}, t_1, \ldots, t_{{\boldsymbol{m}}_\delta }, p_1, \ldots, p_{\boldsymbol{\theta }}$
. To connect them draw a random maximum matching
![]() $\boldsymbol{\Gamma }\left \lbrack{n,\varepsilon }\right \rbrack$
of the complete bipartite graph with vertex classes
$\boldsymbol{\Gamma }\left \lbrack{n,\varepsilon }\right \rbrack$
of the complete bipartite graph with vertex classes
 \begin{align*} V_1= \bigcup _{i=1}^{{\boldsymbol{m}}_\varepsilon } \left \{{a_i}\right \} \times [{\boldsymbol{k}}_i] \qquad \text{and} \qquad V_2= \bigcup _{j=1}^{n}\left \{{x_j}\right \} \times [{\boldsymbol{d}}_j]. \end{align*}
\begin{align*} V_1= \bigcup _{i=1}^{{\boldsymbol{m}}_\varepsilon } \left \{{a_i}\right \} \times [{\boldsymbol{k}}_i] \qquad \text{and} \qquad V_2= \bigcup _{j=1}^{n}\left \{{x_j}\right \} \times [{\boldsymbol{d}}_j]. \end{align*}
For every matching edge
![]() $\{(a_i,h),(x_j,\ell )\}\in \boldsymbol{\Gamma }[n,\varepsilon ]$
,
$\{(a_i,h),(x_j,\ell )\}\in \boldsymbol{\Gamma }[n,\varepsilon ]$
,
![]() $h\in [{\boldsymbol{k}}_i],\ell \in [{\boldsymbol{d}}_j]$
, between a clone of
$h\in [{\boldsymbol{k}}_i],\ell \in [{\boldsymbol{d}}_j]$
, between a clone of
![]() $x_j$
and a clone of
$x_j$
and a clone of
![]() $a_i$
we insert an
$a_i$
we insert an
![]() $a_i$
-
$a_i$
-
![]() $x_j$
-edge into
$x_j$
-edge into
![]() $\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
. Moreover, the check nodes
$\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
. Moreover, the check nodes
![]() $t_1, \ldots, t_{{\boldsymbol{m}}_\delta }$
each independently and uniformly choose three neighbouring variables
$t_1, \ldots, t_{{\boldsymbol{m}}_\delta }$
each independently and uniformly choose three neighbouring variables
![]() $\textbf{i}_{i,1}, \textbf{i}_{i,2}, \textbf{i}_{i,3}$
with replacement among
$\textbf{i}_{i,1}, \textbf{i}_{i,2}, \textbf{i}_{i,3}$
with replacement among
![]() $\left \{{x_1, \ldots, x_n}\right \}$
. Further, check node
$\left \{{x_1, \ldots, x_n}\right \}$
. Further, check node
![]() $p_\ell$
for
$p_\ell$
for
![]() $\ell \in [\boldsymbol{\theta }]$
is adjacent to
$\ell \in [\boldsymbol{\theta }]$
is adjacent to
![]() $x_\ell$
only. Finally, to obtain the random
$x_\ell$
only. Finally, to obtain the random
![]() $(\boldsymbol{\theta } +{\boldsymbol{m}}_\varepsilon +{\boldsymbol{m}}_\delta ) \times n$
-matrix
$(\boldsymbol{\theta } +{\boldsymbol{m}}_\varepsilon +{\boldsymbol{m}}_\delta ) \times n$
-matrix
![]() ${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
from
${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
from
![]() $\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
we let
$\textbf{G}\left \lbrack{n,\varepsilon, \delta, \Theta }\right \rbrack$
we let
 \begin{align} {\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack _{a_{i},x_h}&=\boldsymbol{\chi }_{i, h} \sum _{\ell =1}^{{\boldsymbol{k}}_i}\sum _{s=1}^{{\boldsymbol{d}}_h} {\mathbb{1}} \{(x_h, s), (a_{i}, \ell )\}\in \boldsymbol{\Gamma }\left \lbrack{n,\varepsilon }\right \rbrack \}&&(i\in [{\boldsymbol{m}}_\varepsilon ], h\in [n]), \end{align}
\begin{align} {\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack _{a_{i},x_h}&=\boldsymbol{\chi }_{i, h} \sum _{\ell =1}^{{\boldsymbol{k}}_i}\sum _{s=1}^{{\boldsymbol{d}}_h} {\mathbb{1}} \{(x_h, s), (a_{i}, \ell )\}\in \boldsymbol{\Gamma }\left \lbrack{n,\varepsilon }\right \rbrack \}&&(i\in [{\boldsymbol{m}}_\varepsilon ], h\in [n]), \end{align}
 \begin{align} {\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack _{t_i,x_h}&=\boldsymbol{\chi }_{{\boldsymbol{m}}_{\varepsilon }+i, h} \sum _{\ell =1}^3{\mathbb{1}}\{\textbf{i}_{i,\ell } = h\} &&(i\in [{\boldsymbol{m}}_\delta ],h\in [n]). \end{align}
\begin{align} {\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack _{t_i,x_h}&=\boldsymbol{\chi }_{{\boldsymbol{m}}_{\varepsilon }+i, h} \sum _{\ell =1}^3{\mathbb{1}}\{\textbf{i}_{i,\ell } = h\} &&(i\in [{\boldsymbol{m}}_\delta ],h\in [n]). \end{align}
Applying the Aizenman-Sims-Starr scheme to the matrix
![]() ${\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]$
, we obtain the following variational bound.
${\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]$
, we obtain the following variational bound.
Proposition 4.1.
There exist
![]() $\delta _0\gt 0$
,
$\delta _0\gt 0$
,
![]() $\Theta _0(\varepsilon )\gt 0$
such that for all
$\Theta _0(\varepsilon )\gt 0$
such that for all
![]() $0\lt \delta \lt \delta _0$
and any
$0\lt \delta \lt \delta _0$
and any
![]() $\Theta =\Theta (\varepsilon )\geq \Theta _0(\varepsilon )$
we have
$\Theta =\Theta (\varepsilon )\geq \Theta _0(\varepsilon )$
we have
 \begin{align} &\limsup _{\varepsilon \to 0}\limsup _{n \to \infty } \frac{1}{n} \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack )}\right \rbrack \leq \max _{\alpha, \beta \in [0,1]} \Phi (\alpha ) \nonumber \\[5pt] &\quad + \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(1-K'(\alpha )/k) -\delta + 3\delta \beta ^2 -2\delta \beta ^3. \end{align}
\begin{align} &\limsup _{\varepsilon \to 0}\limsup _{n \to \infty } \frac{1}{n} \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack )}\right \rbrack \leq \max _{\alpha, \beta \in [0,1]} \Phi (\alpha ) \nonumber \\[5pt] &\quad + \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(1-K'(\alpha )/k) -\delta + 3\delta \beta ^2 -2\delta \beta ^3. \end{align}
The proof of Proposition 4.1, carried out in Section 8 in detail, resembles that of the rank formula (1.4), except that we have to accommodate the additional ternary checks
![]() $t_i$
. Their presence is the reason why the optimisation problem on the r.h.s. comes in terms of two variables
$t_i$
. Their presence is the reason why the optimisation problem on the r.h.s. comes in terms of two variables
![]() $\alpha,\beta$
rather than a single variable as (1.4).
$\alpha,\beta$
rather than a single variable as (1.4).
To complete the proof of Proposition 2.3 we need to solve the optimisation problem (4.5). This is the single place where we require that
![]() $\Phi (z)$
takes its unique global max at
$\Phi (z)$
takes its unique global max at
![]() $z=0$
, which ultimately implies that the optimiser of (4.5) is
$z=0$
, which ultimately implies that the optimiser of (4.5) is
![]() $\alpha =\beta =0$
. This fact in turn implies the following.
$\alpha =\beta =0$
. This fact in turn implies the following.
Proposition 4.2.
For any
![]() ${\boldsymbol{d}},{\boldsymbol{k}}$
that satisfy (1.3) there exists
${\boldsymbol{d}},{\boldsymbol{k}}$
that satisfy (1.3) there exists
![]() $\delta _0\gt 0$
such that for all
$\delta _0\gt 0$
such that for all
![]() $0\lt \delta \lt \delta _0$
we have
$0\lt \delta \lt \delta _0$
we have
The proof of Proposition 4.2 can be found in Section 4.2. Finally, in Section 4.3 we will see that Proposition 2.3 is an easy consequence of Propositions 4.1 and 4.2.
4.2 Proof of Proposition 4.2
Let
Assuming (1.3), we are going to prove that for small enough
![]() $\delta$
,
$\delta$
,
whence the assertion is immediate.
The
![]() $C^1$
-function
$C^1$
-function
![]() $\tilde \Phi _\delta$
attains its maximum either at a boundary point of the compact domain
$\tilde \Phi _\delta$
attains its maximum either at a boundary point of the compact domain
![]() $[0,1]^2$
or at a point where the partial derivatives vanish. Beginning with the former, we consider four cases.
$[0,1]^2$
or at a point where the partial derivatives vanish. Beginning with the former, we consider four cases.
-
Case 1:
 $\alpha =0$
We have(4.7)Expanding the exponential function, we see that
$\alpha =0$
We have(4.7)Expanding the exponential function, we see that \begin{align} \tilde{\Phi }_\delta (0, \beta ) = \tilde{\Phi }_\delta (0,0) + 3\delta \beta ^2 - 2\delta \beta ^3 -(1-\exp\!\left ({-3\delta \beta ^2}\right )). \end{align}
\begin{align} \tilde{\Phi }_\delta (0, \beta ) = \tilde{\Phi }_\delta (0,0) + 3\delta \beta ^2 - 2\delta \beta ^3 -(1-\exp\!\left ({-3\delta \beta ^2}\right )). \end{align}
 $3\delta \beta ^2 - 2\delta \beta ^3 -(1-\exp\!\left ({-3\delta \beta ^2}\right )) = - 2\delta \beta ^3 + O_\delta (\delta ^2\beta ^4)$
. Since
$3\delta \beta ^2 - 2\delta \beta ^3 -(1-\exp\!\left ({-3\delta \beta ^2}\right )) = - 2\delta \beta ^3 + O_\delta (\delta ^2\beta ^4)$
. Since
 $- 2\delta \beta ^3 + O_\delta (\delta ^2\beta ^4)$
is non-positive for all
$- 2\delta \beta ^3 + O_\delta (\delta ^2\beta ^4)$
is non-positive for all
 $\beta \in [0,1]$
, (4.7) yields
$\beta \in [0,1]$
, (4.7) yields
 $\max _\beta \tilde{\Phi }_\delta (0,\beta )=\tilde \Phi _\delta (0,0)$
for all small enough
$\max _\beta \tilde{\Phi }_\delta (0,\beta )=\tilde \Phi _\delta (0,0)$
for all small enough
 $\delta \gt 0$
.
$\delta \gt 0$
.
-
Case 2:
 $\beta =0$
The assumption (1.3) ensures that
$\beta =0$
The assumption (1.3) ensures that
 $\Phi$
is maximised in
$\Phi$
is maximised in
 $0$
. Therefore, as
$0$
. Therefore, as
 $\tilde{\Phi }_\delta (\alpha,0) = \Phi (\alpha )-\delta$
, the maximum on
$\tilde{\Phi }_\delta (\alpha,0) = \Phi (\alpha )-\delta$
, the maximum on
 $\left \{{(\alpha,0) \;:\; \alpha \in [0,1]}\right \}$
is attained in
$\left \{{(\alpha,0) \;:\; \alpha \in [0,1]}\right \}$
is attained in
 $\alpha =0$
.
$\alpha =0$
. -
Case 3:
 $\alpha =1$
We obtainAgain, expanding the exponential, we see that for sufficiently small
$\alpha =1$
We obtainAgain, expanding the exponential, we see that for sufficiently small \begin{align*}\quad {\tilde{\Phi }_\delta (1,\beta )} &=\Phi (1)+ \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(0) - \delta + 3 \delta \beta ^2 - 2 \delta \beta ^3 =\exp\!\left ({-3\delta \beta ^2}\right )D(0)\\[5pt] &\quad + \delta (3\beta ^2 - 2 \beta ^3-1). \end{align*}
\begin{align*}\quad {\tilde{\Phi }_\delta (1,\beta )} &=\Phi (1)+ \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(0) - \delta + 3 \delta \beta ^2 - 2 \delta \beta ^3 =\exp\!\left ({-3\delta \beta ^2}\right )D(0)\\[5pt] &\quad + \delta (3\beta ^2 - 2 \beta ^3-1). \end{align*}
 $\delta$
,
$\delta$
,
 $\tilde{\Phi }_\delta (1,\beta ) \leq \tilde{\Phi }_\delta (1,0) = \Phi (1) - \delta$
. Thanks to assumption (1.3), this yields
$\tilde{\Phi }_\delta (1,\beta ) \leq \tilde{\Phi }_\delta (1,0) = \Phi (1) - \delta$
. Thanks to assumption (1.3), this yields
 $\max _\beta \tilde{\Phi }_\delta (1,\beta )=\tilde \Phi _\delta (0,0)$
for all small enough
$\max _\beta \tilde{\Phi }_\delta (1,\beta )=\tilde \Phi _\delta (0,0)$
for all small enough
 $\delta \gt 0$
.
$\delta \gt 0$
.
-
Case 4:
 $\beta =1$
We have(4.8)Because
$\beta =1$
We have(4.8)Because \begin{equation} \tilde{\Phi }_\delta (\alpha, 1) = \Phi (\alpha ) - (1-\exp\!\left ({-3\delta }\right ))D\left ({1-\frac{K'(\alpha )}{k}}\right ). \end{equation}
\begin{equation} \tilde{\Phi }_\delta (\alpha, 1) = \Phi (\alpha ) - (1-\exp\!\left ({-3\delta }\right ))D\left ({1-\frac{K'(\alpha )}{k}}\right ). \end{equation}
 $D$
and
$D$
and
 $K'$
are continuous on
$K'$
are continuous on
 $[0,1]$
due to the assumption
$[0,1]$
due to the assumption
 $\mathbb{E}[{\boldsymbol{d}}^2]+\mathbb{E}[{\boldsymbol{k}}^2]\lt \infty$
, for any
$\mathbb{E}[{\boldsymbol{d}}^2]+\mathbb{E}[{\boldsymbol{k}}^2]\lt \infty$
, for any
 $\zeta \gt 0$
there exists
$\zeta \gt 0$
there exists
 $\hat{\alpha }\gt 0$
such that
$\hat{\alpha }\gt 0$
such that
 $D(1-K'(\alpha )/k) \gt 1-\zeta$
for all
$D(1-K'(\alpha )/k) \gt 1-\zeta$
for all
 $0\lt \alpha \lt \hat{\alpha }$
. Therefore, (4.8) shows that for small enough
$0\lt \alpha \lt \hat{\alpha }$
. Therefore, (4.8) shows that for small enough
 $\delta \gt 0$
and
$\delta \gt 0$
and
 $0\lt \alpha \lt \hat{\alpha }$
we have
$0\lt \alpha \lt \hat{\alpha }$
we have
 $\tilde{\Phi }_\delta (\alpha, 1) \lt \tilde{\Phi }_\delta (\alpha,0)\leq \tilde{\Phi }_\delta (0,0)$
. On the other hand, for
$\tilde{\Phi }_\delta (\alpha, 1) \lt \tilde{\Phi }_\delta (\alpha,0)\leq \tilde{\Phi }_\delta (0,0)$
. On the other hand, for
 $\hat{\alpha }\leq \alpha \leq 1$
the difference
$\hat{\alpha }\leq \alpha \leq 1$
the difference
 $\Phi (\alpha )-\Phi (0)$
is uniformly negative because of our assumption (1.3) that
$\Phi (\alpha )-\Phi (0)$
is uniformly negative because of our assumption (1.3) that
 $\Phi$
attains its unique global maximum at
$\Phi$
attains its unique global maximum at
 $\alpha =0$
. Hence, for
$\alpha =0$
. Hence, for
 $\delta$
small enough and
$\delta$
small enough and
 $\hat{\alpha }\le \alpha \leq 1$
we obtain
$\hat{\alpha }\le \alpha \leq 1$
we obtain
 $\tilde{\Phi }_\delta (\alpha, 1) \lt \tilde{\Phi }_\delta (0,0)$
.
$\tilde{\Phi }_\delta (\alpha, 1) \lt \tilde{\Phi }_\delta (0,0)$
.
Combining Cases 1–4, we obtain
Moving on to the interior of
![]() $[0,1]^2$
, we calculate the derivatives
$[0,1]^2$
, we calculate the derivatives
 \begin{align*} \frac{\partial \tilde \Phi _\delta }{\partial \alpha } &= \Phi '(\alpha ) + \left ({1-\exp\!\left ({-3\delta \beta ^2}\right )}\right ) \frac{K''(\alpha )}{k}D'(1-K'(\alpha )/k) \\[5pt] &= \frac{K''(\alpha )}{k} \left ({d(1-\alpha )-\exp\!\left ({-3\delta \beta ^2}\right )D'(1-K'(\alpha )/k)}\right ),\\[5pt] \frac{\partial \tilde \Phi _\delta }{\partial \beta } &= 6 \delta \beta \left ({1-\beta -\exp\!\left ({-3\delta \beta ^2}\right )D(1-K'(\alpha )/k)}\right ). \end{align*}
\begin{align*} \frac{\partial \tilde \Phi _\delta }{\partial \alpha } &= \Phi '(\alpha ) + \left ({1-\exp\!\left ({-3\delta \beta ^2}\right )}\right ) \frac{K''(\alpha )}{k}D'(1-K'(\alpha )/k) \\[5pt] &= \frac{K''(\alpha )}{k} \left ({d(1-\alpha )-\exp\!\left ({-3\delta \beta ^2}\right )D'(1-K'(\alpha )/k)}\right ),\\[5pt] \frac{\partial \tilde \Phi _\delta }{\partial \beta } &= 6 \delta \beta \left ({1-\beta -\exp\!\left ({-3\delta \beta ^2}\right )D(1-K'(\alpha )/k)}\right ). \end{align*}
Hence, potential maximisers
![]() $(\alpha,\beta )$
in the interior of
$(\alpha,\beta )$
in the interior of
![]() $[0,1]^2$
satisfy
$[0,1]^2$
satisfy
Substituting (4.10) into
![]() $\tilde \Phi _\delta$
, we obtain
$\tilde \Phi _\delta$
, we obtain
 \begin{align} \nonumber \tilde{\Phi }_\delta (\alpha, \beta )&= \Phi (\alpha ) - \delta + \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(1-K'(\alpha )/k) + 3\delta \beta ^2 -2\delta \beta ^3\\[5pt] &=\Phi (\alpha ) - \delta + (1-\beta )(1-\exp\!\left ({3\delta \beta ^2}\right ))+ 3\delta \beta ^2 -2\delta \beta ^3 \nonumber \\[5pt] &\leq \Phi (\alpha ) - \delta - 3\delta \beta ^2 (1-\beta )+ 3\delta \beta ^2 -2\delta \beta ^3 = \Phi (\alpha )-\delta +\delta \beta ^3. \end{align}
\begin{align} \nonumber \tilde{\Phi }_\delta (\alpha, \beta )&= \Phi (\alpha ) - \delta + \left ({\exp\!\left ({-3\delta \beta ^2}\right )-1}\right )D(1-K'(\alpha )/k) + 3\delta \beta ^2 -2\delta \beta ^3\\[5pt] &=\Phi (\alpha ) - \delta + (1-\beta )(1-\exp\!\left ({3\delta \beta ^2}\right ))+ 3\delta \beta ^2 -2\delta \beta ^3 \nonumber \\[5pt] &\leq \Phi (\alpha ) - \delta - 3\delta \beta ^2 (1-\beta )+ 3\delta \beta ^2 -2\delta \beta ^3 = \Phi (\alpha )-\delta +\delta \beta ^3. \end{align}
To estimate the r.h.s. we consider the cases of small and large
![]() $\alpha$
separately. Specifically, by continuity for any
$\alpha$
separately. Specifically, by continuity for any
![]() $\zeta \gt 0$
there is
$\zeta \gt 0$
there is
![]() $0\lt \hat{\alpha }\lt \delta$
such that
$0\lt \hat{\alpha }\lt \delta$
such that
![]() $D(1-K'(\alpha )/k)\gt 1-\zeta$
for all
$D(1-K'(\alpha )/k)\gt 1-\zeta$
for all
![]() $0\lt \alpha \lt \hat{\alpha }$
.
$0\lt \alpha \lt \hat{\alpha }$
.
-
Case 1:
 $0\lt \alpha \lt \hat{\alpha }$
Since
$0\lt \alpha \lt \hat{\alpha }$
Since
 $D(1-K'(\alpha )/k)\gt 1-\zeta$
, (4.10) implies that for
$D(1-K'(\alpha )/k)\gt 1-\zeta$
, (4.10) implies that for
 $\beta \gt 0$
In particular, small
$\beta \gt 0$
In particular, small \begin{equation*}1-\beta \gt (1-3\delta \beta ^2) (1-\zeta ) = 1 - \zeta - 3\delta \beta ^2(1-\zeta ).\end{equation*}
\begin{equation*}1-\beta \gt (1-3\delta \beta ^2) (1-\zeta ) = 1 - \zeta - 3\delta \beta ^2(1-\zeta ).\end{equation*}
 $\hat \alpha$
implies that also
$\hat \alpha$
implies that also
 $\beta$
is small. More precisely, after choosing
$\beta$
is small. More precisely, after choosing
 $\delta,\zeta$
small enough, we may assume that
$\delta,\zeta$
small enough, we may assume that
 $\beta \lt \hat{\beta }$
for any fixed
$\beta \lt \hat{\beta }$
for any fixed
 $\hat{\beta }\gt 0$
. In this case, we may thus restrict to solutions
$\hat{\beta }\gt 0$
. In this case, we may thus restrict to solutions
 $(\alpha, \beta ) \in (0,1)^2$
to (4.10) where both coordinates are sufficiently small. Also here, we distinguish three cases that all lead to contradictions.
$(\alpha, \beta ) \in (0,1)^2$
to (4.10) where both coordinates are sufficiently small. Also here, we distinguish three cases that all lead to contradictions.-
(A) If the solution satisfies
 $\alpha =\beta$
, consider the functionwhose zeros determine the solutions to the right equation in (4.10) under the assumption
$\alpha =\beta$
, consider the functionwhose zeros determine the solutions to the right equation in (4.10) under the assumption \begin{equation*}x \mapsto 1-x-\exp\!\left ({-3\delta x^2}\right ) D(1-K'(x)/k)\end{equation*}
\begin{equation*}x \mapsto 1-x-\exp\!\left ({-3\delta x^2}\right ) D(1-K'(x)/k)\end{equation*}
 $\alpha =\beta$
. Its value is zero at
$\alpha =\beta$
. Its value is zero at
 $x=0$
and it has derivativewhich is negative in a neighbourhood of
$x=0$
and it has derivativewhich is negative in a neighbourhood of \begin{equation*}-1+6\delta x \exp\!\left ({-3\delta x^2}\right ) D(1-K'(x)/k) + \exp\!\left ({-3\delta x^2}\right ) D'(1-K'(x)/k)\frac {K''(x)}{k},\end{equation*}
\begin{equation*}-1+6\delta x \exp\!\left ({-3\delta x^2}\right ) D(1-K'(x)/k) + \exp\!\left ({-3\delta x^2}\right ) D'(1-K'(x)/k)\frac {K''(x)}{k},\end{equation*}
 $x=0$
. Thus
$x=0$
. Thus
 $(\alpha, \alpha )$
cannot be a solution to (4.10) for
$(\alpha, \alpha )$
cannot be a solution to (4.10) for
 $\alpha \in (0, \hat{\alpha })$
.
$\alpha \in (0, \hat{\alpha })$
.
-
(B) Assume now that
 $\alpha \lt \beta$
. Then the right equation of (4.10) yieldsNow since
$\alpha \lt \beta$
. Then the right equation of (4.10) yieldsNow since \begin{align*} 1-\beta \gt \exp\!\left ({-3\delta \beta ^2}\right )D\left ({1-K'(\beta )/k}\right ) \gt \left ({1-3 \delta \beta ^2}\right ) \left ({1- \frac{d}{k}K'(\beta )}\right ). \end{align*}
\begin{align*} 1-\beta \gt \exp\!\left ({-3\delta \beta ^2}\right )D\left ({1-K'(\beta )/k}\right ) \gt \left ({1-3 \delta \beta ^2}\right ) \left ({1- \frac{d}{k}K'(\beta )}\right ). \end{align*}
 ${\boldsymbol{k}} \geq 3$
,
${\boldsymbol{k}} \geq 3$
,
 $K'(\beta ) = O_\beta (\beta ^2)$
. But then the above equation yields a contradiction for
$K'(\beta ) = O_\beta (\beta ^2)$
. But then the above equation yields a contradiction for
 $\beta$
small enough and thus
$\beta$
small enough and thus
 $(\alpha, \beta ) \in (0,\hat \alpha ) \times (0,\hat \beta )$
with
$(\alpha, \beta ) \in (0,\hat \alpha ) \times (0,\hat \beta )$
with
 $\alpha \lt \beta$
is no possible solution.
$\alpha \lt \beta$
is no possible solution.
-
(C) Finally, if
 $\alpha \gt \beta$
, the left equation of (4.10) yieldsNow since
$\alpha \gt \beta$
, the left equation of (4.10) yieldsNow since \begin{align*} d\left ({1-\alpha }\right ) \gt \exp\!\left ({-3\delta \alpha ^2}\right )D'\left ({1-K'(\alpha )/k}\right ) \gt d\left ({1-3 \delta \alpha ^2}\right ) \left ({1- \frac{\mathbb{E}\left \lbrack{{\boldsymbol{d}}^2}\right \rbrack }{dk}K'(\alpha )}\right ). \end{align*}
\begin{align*} d\left ({1-\alpha }\right ) \gt \exp\!\left ({-3\delta \alpha ^2}\right )D'\left ({1-K'(\alpha )/k}\right ) \gt d\left ({1-3 \delta \alpha ^2}\right ) \left ({1- \frac{\mathbb{E}\left \lbrack{{\boldsymbol{d}}^2}\right \rbrack }{dk}K'(\alpha )}\right ). \end{align*}
 ${\boldsymbol{k}} \geq 3$
,
${\boldsymbol{k}} \geq 3$
,
 $K'(\alpha ) = O_\alpha (\alpha ^2)$
. But then the above equation yields a contradiction for
$K'(\alpha ) = O_\alpha (\alpha ^2)$
. But then the above equation yields a contradiction for
 $\alpha$
small enough and thus
$\alpha$
small enough and thus
 $(\alpha, \beta ) \in (0,\hat \alpha ) \times (0,\hat \beta )$
with
$(\alpha, \beta ) \in (0,\hat \alpha ) \times (0,\hat \beta )$
with
 $\alpha \gt \beta$
is no possible solution.
$\alpha \gt \beta$
is no possible solution.
Hence, (4.10) has no solution with
 $0\lt \alpha \lt \hat{\alpha }$
.
$0\lt \alpha \lt \hat{\alpha }$
. -
-
Case 2:
 $\hat{\alpha }\leq \alpha \lt 1$
because
$\hat{\alpha }\leq \alpha \lt 1$
because
 $\Phi (\alpha )\lt \Phi (0)$
for all
$\Phi (\alpha )\lt \Phi (0)$
for all
 $0\lt \alpha \leq 1$
, (4.11) shows that we can choose
$0\lt \alpha \leq 1$
, (4.11) shows that we can choose
 $\delta$
small enough so that
$\delta$
small enough so that
 $\tilde \Phi _\delta (\alpha,\beta )\lt \tilde{\Phi }_\delta (0,0)$
for all
$\tilde \Phi _\delta (\alpha,\beta )\lt \tilde{\Phi }_\delta (0,0)$
for all
 $\alpha \geq \hat{\alpha }$
and all
$\alpha \geq \hat{\alpha }$
and all
 $\beta \in [0,1]$
.
$\beta \in [0,1]$
.
4.3 Proof of Proposition 2.3
Combining Propositions 4.1 and 4.2, we see that
The only (small) missing piece is that we still need to extend this result to the original random matrix
![]() $\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
based on the simple random factor graph
$\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
based on the simple random factor graph
![]() $\mathbb{G}$
. To this end we apply the following lemma.
$\mathbb{G}$
. To this end we apply the following lemma.
Lemma 4.3 ([Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 4.8]). For any fixed
![]() $\Theta \gt 0$
there exists a coupling of
$\Theta \gt 0$
there exists a coupling of
![]() ${\boldsymbol{A}}$
and
${\boldsymbol{A}}$
and
![]() ${\boldsymbol{A}}\left \lbrack{n,\varepsilon,0,\Theta }\right \rbrack$
such that
${\boldsymbol{A}}\left \lbrack{n,\varepsilon,0,\Theta }\right \rbrack$
such that
Let
![]() ${\boldsymbol{A}}_{[\lfloor \delta n\rfloor ]}$
be the matrix obtained from
${\boldsymbol{A}}_{[\lfloor \delta n\rfloor ]}$
be the matrix obtained from
![]() ${\boldsymbol{A}}$
by adding
${\boldsymbol{A}}$
by adding
![]() $\lfloor \delta n\rfloor$
random ternary equations. Combining (4.12) with Corollary 4.3, we obtain
$\lfloor \delta n\rfloor$
random ternary equations. Combining (4.12) with Corollary 4.3, we obtain
Furthermore, since changing a single edge of the Tanner graph
![]() ${\boldsymbol{G}}$
or a single entry of
${\boldsymbol{G}}$
or a single entry of
![]() ${\boldsymbol{A}}$
can change the rank by at most one, the Azuma–Hoeffding inequality shows that
${\boldsymbol{A}}$
can change the rank by at most one, the Azuma–Hoeffding inequality shows that
![]() $\text{nul}({\boldsymbol{A}}_{[\lfloor \delta n\rfloor ]})$
is tightly concentrated. Thus, (4.13) implies
$\text{nul}({\boldsymbol{A}}_{[\lfloor \delta n\rfloor ]})$
is tightly concentrated. Thus, (4.13) implies
Finally, combining (4.14) with Proposition 3.7, we conclude that
which implies the assertion because
![]() $\text{nul}(\mathbb{A}_{[\lfloor \delta n\rfloor ]})\leq n$
deterministically.
$\text{nul}(\mathbb{A}_{[\lfloor \delta n\rfloor ]})\leq n$
deterministically.
5. Proof of Proposition 2.4
We now go on to prove that if the matrix
![]() $\mathbb{A}[\boldsymbol{\theta }_0]$
obtained from
$\mathbb{A}[\boldsymbol{\theta }_0]$
obtained from
![]() $\mathbb{A}$
by adding a few random unary checks had many frozen coordinates, then the nullity of
$\mathbb{A}$
by adding a few random unary checks had many frozen coordinates, then the nullity of
![]() $\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
would be greater than permitted by Proposition 2.3; we use an argument similar to [Reference Ayre, Coja-Oghlan, Gao and Müller6, proof of Proposition 2.7]. Invoking Corollary 3.5 will then complete the proof of Proposition 2.4.
$\mathbb{A}_{[\lfloor \delta n\rfloor ]}$
would be greater than permitted by Proposition 2.3; we use an argument similar to [Reference Ayre, Coja-Oghlan, Gao and Müller6, proof of Proposition 2.7]. Invoking Corollary 3.5 will then complete the proof of Proposition 2.4.
Lemma 5.1.
Assume that for some
![]() $\Theta \gt 0$
and
$\Theta \gt 0$
and
![]() $\boldsymbol{\theta }_0\sim \text{unif}([\Theta ])$
we have
$\boldsymbol{\theta }_0\sim \text{unif}([\Theta ])$
we have
Then for all
![]() $\delta \gt 0$
we have
$\delta \gt 0$
we have
Proof. For an integer
![]() $\ell \geq 0$
obtain
$\ell \geq 0$
obtain
![]() $\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
from
$\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
from
![]() $\mathbb{A}[\boldsymbol{\theta }_0]$
by adding
$\mathbb{A}[\boldsymbol{\theta }_0]$
by adding
![]() $\ell$
random ternary equations. Since
$\ell$
random ternary equations. Since
![]() $\text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]} \geq \text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]}[\boldsymbol{\theta }_0]\geq \text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]}-\boldsymbol{\theta }_0$
, for any fixed
$\text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]} \geq \text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]}[\boldsymbol{\theta }_0]\geq \text{nul}\mathbb{A}_{[\lfloor \delta n\rfloor ]}-\boldsymbol{\theta }_0$
, for any fixed
![]() $\Theta \gt 0$
,
$\Theta \gt 0$
,
For fixed large
![]() $n$
, we now estimate the nullity of
$n$
, we now estimate the nullity of
![]() $\mathbb{A}_{[\delta n]}[\boldsymbol{\theta }_0]$
under the assumption that
$\mathbb{A}_{[\delta n]}[\boldsymbol{\theta }_0]$
under the assumption that
Because adding equations can only increase the set of frozen variables, we have
![]() $\mathfrak{F}(\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0])\subseteq \mathfrak{F}(\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0])$
for all
$\mathfrak{F}(\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0])\subseteq \mathfrak{F}(\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0])$
for all
![]() $\ell \geq 0$
. Therefore, (5.2) implies that
$\ell \geq 0$
. Therefore, (5.2) implies that
We now claim that for any
![]() $\delta \gt 0$
$\delta \gt 0$
To prove (5.4) it suffices to show that for any
![]() $\ell \geq 0$
,
$\ell \geq 0$
,
Indeed, we obtain (5.4) from (5.5) and the nullity formula
![]() $n^{-1}\mathbb{E}[\text{nul}\mathbb{A}_{[0]}[\boldsymbol{\theta }_0]]=n^{-1}\mathbb{E}[\text{nul}\mathbb{A}]+o(1)=1-d/k+o(1)$
from (1.4) by writing a telescoping sum.
$n^{-1}\mathbb{E}[\text{nul}\mathbb{A}_{[0]}[\boldsymbol{\theta }_0]]=n^{-1}\mathbb{E}[\text{nul}\mathbb{A}]+o(1)=1-d/k+o(1)$
from (1.4) by writing a telescoping sum.
To establish (5.5) we observe that
![]() $\text{nul}\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]-\text{nul}\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]\geq -1$
because we obtain
$\text{nul}\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]-\text{nul}\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]\geq -1$
because we obtain
![]() $\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]$
from
$\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]$
from
![]() $\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
by adding a single ternary equation. Furthermore, if
$\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
by adding a single ternary equation. Furthermore, if
![]() $|\mathfrak{F}(\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0])|\geq \zeta n$
, then with probability at least
$|\mathfrak{F}(\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0])|\geq \zeta n$
, then with probability at least
![]() $\zeta ^3$
all three variables of the new ternary equation are frozen in
$\zeta ^3$
all three variables of the new ternary equation are frozen in
![]() $\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
, in which case
$\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
, in which case
![]() $\text{nul}\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]=\text{nul}\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
. Hence, (5.4) follows from (5.5), which follows from (5.3). Finally, combining (5.1) and (5.4) completes the proof.
$\text{nul}\mathbb{A}_{[\ell +1]}[\boldsymbol{\theta }_0]=\text{nul}\mathbb{A}_{[\ell ]}[\boldsymbol{\theta }_0]$
. Hence, (5.4) follows from (5.5), which follows from (5.3). Finally, combining (5.1) and (5.4) completes the proof.
6. Proof of Proposition 2.5
The proof proceeds very differently depending on whether the coefficients
![]() $\chi _1,\ldots,\chi _{k_0}$
are identical or not. The following two lemmas summarise the analyses of the two cases.
$\chi _1,\ldots,\chi _{k_0}$
are identical or not. The following two lemmas summarise the analyses of the two cases.
Lemma 6.1.
For any prime power
![]() $q$
and any
$q$
and any
![]() $\chi \in \mathbb{F}_q^*$
the
$\chi \in \mathbb{F}_q^*$
the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{M}_q(\chi,\chi,\chi )$
possesses a basis
$\mathfrak{M}_q(\chi,\chi,\chi )$
possesses a basis
![]() $(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors
$(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors
![]() $\mathfrak{b}_i\in \mathbb{Z}^{\mathbb{F}_q^*}$
for all
$\mathfrak{b}_i\in \mathbb{Z}^{\mathbb{F}_q^*}$
for all
![]() $i\in [q-1]$
such that
$i\in [q-1]$
such that
Furthermore, for any
![]() $k_0\gt 3$
we have
$k_0\gt 3$
we have
![]() $\mathfrak{M}_q\underbrace{\left ({\chi,\ldots,\chi }\right )}_{\mbox{$k_0$ times}}=\mathfrak{M}_q(\chi,\chi,\chi ).$
$\mathfrak{M}_q\underbrace{\left ({\chi,\ldots,\chi }\right )}_{\mbox{$k_0$ times}}=\mathfrak{M}_q(\chi,\chi,\chi ).$
Lemma 6.2.
Suppose that
![]() $q$
is a prime power, that
$q$
is a prime power, that
![]() $k_0\geq 3$
and that
$k_0\geq 3$
and that
![]() $\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
satisfy
$\chi _1,\ldots,\chi _{k_0}\in \mathbb{F}_q^*$
satisfy
![]() $|\{\chi _1,\ldots,\chi _{k_0}\}|\geq 2$
. Then
$|\{\chi _1,\ldots,\chi _{k_0}\}|\geq 2$
. Then
Furthermore,
![]() $\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
possesses a basis
$\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
possesses a basis
![]() $(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors
$(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
of non-negative integer vectors
![]() $\mathfrak{b}_i\in \mathbb{Z}^{\mathbb{F}_q^*}$
such that
$\mathfrak{b}_i\in \mathbb{Z}^{\mathbb{F}_q^*}$
such that
Clearly, Proposition 2.5 is an immediate consequence of Lemmas 6.1 and 6.2 . We proceed to prove the former in Section 6.1 and the latter in Section 6.2.
6.1 Proof of Lemma 6.1
Because we can just factor out any scalar, it suffices to consider the module
Being a submodule of the free
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
,
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
,
![]() $\mathfrak{M}$
is free, but it is not entirely self-evident that a basis with the additional properties stated in Lemma 6.1 exists. Indeed, while it is easy enough to come up with
$\mathfrak{M}$
is free, but it is not entirely self-evident that a basis with the additional properties stated in Lemma 6.1 exists. Indeed, while it is easy enough to come up with
![]() $q-1$
linearly independent vectors in
$q-1$
linearly independent vectors in
![]() $\mathfrak{M}$
that all have
$\mathfrak{M}$
that all have
![]() $\ell _1$
-norm bounded by
$\ell _1$
-norm bounded by
![]() $3$
, it is more difficult to show that these vectors generate
$3$
, it is more difficult to show that these vectors generate
![]() $\mathfrak{M}$
. In the proof of Lemma 6.1, we sidestep this difficulty by working with two sets of vectors
$\mathfrak{M}$
. In the proof of Lemma 6.1, we sidestep this difficulty by working with two sets of vectors
![]() $\mathcal{B}_1$
and
$\mathcal{B}_1$
and
![]() $\mathcal{B}_2$
. The first set
$\mathcal{B}_2$
. The first set
![]() $\mathcal{B}_1$
is easily seen to generate
$\mathcal{B}_1$
is easily seen to generate
![]() $\mathfrak{M}$
, while
$\mathfrak{M}$
, while
![]() $\mathcal{B}_2$
is a set of linearly independent vectors in
$\mathcal{B}_2$
is a set of linearly independent vectors in
![]() $\mathfrak{M}$
with
$\mathfrak{M}$
with
![]() $\ell _1$
-norms bounded by
$\ell _1$
-norms bounded by
![]() $3$
. To argue that
$3$
. To argue that
![]() $\mathcal{B}_2$
generates
$\mathcal{B}_2$
generates
![]() $\mathfrak{M}$
, too, it then suffices to show that the determinant of the change of basis matrix equals one.
$\mathfrak{M}$
, too, it then suffices to show that the determinant of the change of basis matrix equals one.
To interpret the bases as subsets of
![]() $\mathbb{Z}^{q-1}$
rather than
$\mathbb{Z}^{q-1}$
rather than
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
in the following, we fix some notation for the elements of
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
in the following, we fix some notation for the elements of
![]() $\mathbb{F}_q$
. Throughout this section, we let
$\mathbb{F}_q$
. Throughout this section, we let
![]() $q=p^\ell$
for a prime
$q=p^\ell$
for a prime
![]() $p$
and
$p$
and
![]() $\ell \in \mathbb{N}$
. If
$\ell \in \mathbb{N}$
. If
![]() $\ell =1$
, we regard
$\ell =1$
, we regard
![]() $\mathbb{F}_q$
as the set
$\mathbb{F}_q$
as the set
![]() $\{0, \ldots, p-1\}$
with
$\{0, \ldots, p-1\}$
with
![]() $\mod p$
arithmetic. If
$\mod p$
arithmetic. If
![]() $\ell \geq 2$
, the field elements can be written as
$\ell \geq 2$
, the field elements can be written as
with
![]() $\mod g({\mathbb{X}})$
arithmetic for a prime polynomial
$\mod g({\mathbb{X}})$
arithmetic for a prime polynomial
![]() $g({\mathbb{X}})\in \mathbb{F}_p[{\mathbb{X}}]$
of degree
$g({\mathbb{X}})\in \mathbb{F}_p[{\mathbb{X}}]$
of degree
![]() $\ell$
. Exploiting this representation of the field elements as polynomials, we define the length len
$\ell$
. Exploiting this representation of the field elements as polynomials, we define the length len
![]() $(a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1})$
of an element of
$(a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1})$
of an element of
![]() $\mathbb{F}_q$
to be the number of its non-zero coefficients. Finally, let
$\mathbb{F}_q$
to be the number of its non-zero coefficients. Finally, let
be the set of all elements of
![]() $\mathbb{F}_q$
with length at least two. Of course, if
$\mathbb{F}_q$
with length at least two. Of course, if
![]() $\ell = 1$
,
$\ell = 1$
,
![]() $\mathbb{F}_q^{(\geq 2)}$
is empty.
$\mathbb{F}_q^{(\geq 2)}$
is empty.
Recall that we view
![]() $\mathfrak{M}$
as a subset of
$\mathfrak{M}$
as a subset of
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
that is generated by the vectors
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
that is generated by the vectors
 \begin{align*} \left ({\sum _{i=1}^{k_0}{\mathbb{1}}\left \{{\sigma _i=s}\right \}}\right )_{s\in \mathbb{F}_q^*}, \quad \sigma \in{\mathcal{S}_q(1, \ldots, 1)}. \end{align*}
\begin{align*} \left ({\sum _{i=1}^{k_0}{\mathbb{1}}\left \{{\sigma _i=s}\right \}}\right )_{s\in \mathbb{F}_q^*}, \quad \sigma \in{\mathcal{S}_q(1, \ldots, 1)}. \end{align*}
In the above representation, the generators are indexed by
![]() $\mathbb{F}_q^*$
rather than by the set
$\mathbb{F}_q^*$
rather than by the set
![]() $[q-1]$
. But to carry out the determinant calculation, it is immensely useful to represent both
$[q-1]$
. But to carry out the determinant calculation, it is immensely useful to represent both
![]() $\mathcal{B}_1$
and
$\mathcal{B}_1$
and
![]() $\mathcal{B}_2$
as matrices with a convenient structure. Hence, there is ambiguity in the choice of a bijection
$\mathcal{B}_2$
as matrices with a convenient structure. Hence, there is ambiguity in the choice of a bijection
![]() $f\;:\;\mathbb{F}_q^\ast \to \{1, \ldots, q-1\}$
that maps the non-zero elements of
$f\;:\;\mathbb{F}_q^\ast \to \{1, \ldots, q-1\}$
that maps the non-zero elements of
![]() $\mathbb{F}_q$
to coordinates in
$\mathbb{F}_q$
to coordinates in
![]() $\mathbb{Z}^{\mathbb{F}_q^*}$
. To put a clear structure to the matrices in this subsection, we will soon choose
$\mathbb{Z}^{\mathbb{F}_q^*}$
. To put a clear structure to the matrices in this subsection, we will soon choose
![]() $f$
in a particular way. With the above notation, we will from now on fix a bijection
$f$
in a particular way. With the above notation, we will from now on fix a bijection
![]() $f$
that is monotonically decreasing with respect to the length function on
$f$
that is monotonically decreasing with respect to the length function on
![]() $\mathbb{F}_q^\ast$
: If len
$\mathbb{F}_q^\ast$
: If len
![]() $(h_1) \lt$
len
$(h_1) \lt$
len
![]() $(h_2)$
for
$(h_2)$
for
![]() $h_1, h_2 \in \mathbb{F}_q^\ast$
, then
$h_1, h_2 \in \mathbb{F}_q^\ast$
, then
![]() $f(h_1) \gt f(h_2)$
. More precisely,
$f(h_1) \gt f(h_2)$
. More precisely,
![]() $f$
maps the
$f$
maps the
![]() $(p-1)^\ell$
elements in
$(p-1)^\ell$
elements in
![]() $\mathbb{F}_q^\ast$
of maximal length
$\mathbb{F}_q^\ast$
of maximal length
![]() $\ell$
to the interval
$\ell$
to the interval
![]() $[(p-1)^\ell ]$
, the
$[(p-1)^\ell ]$
, the
![]() $\ell (p-1)^{\ell -1}$
elements of length
$\ell (p-1)^{\ell -1}$
elements of length
![]() $\ell -1$
to the interval
$\ell -1$
to the interval
![]() $\{(p-1)^\ell +1, \ldots, (p-1)^\ell +\ell (p-1)^{\ell -1}\}$
, and so on. For elements of length one, we further specify that
$\{(p-1)^\ell +1, \ldots, (p-1)^\ell +\ell (p-1)^{\ell -1}\}$
, and so on. For elements of length one, we further specify that
For our purposes, there is no need to fully specify the values of
![]() $f$
within sets of constant length greater than one, but one could follow the lexicographic order, for example. The benefit of such an ordering will become apparent in the next two subsections.
$f$
within sets of constant length greater than one, but one could follow the lexicographic order, for example. The benefit of such an ordering will become apparent in the next two subsections.
6.1.1 First basis
 $\mathcal{B}_1$
$\mathcal{B}_1$
The idea behind the first set
![]() $\mathcal{B}_1$
is that it consists of vectors whose coordinates can be easily seen to correspond to element statistics of a valid solution while ignoring the
$\mathcal{B}_1$
is that it consists of vectors whose coordinates can be easily seen to correspond to element statistics of a valid solution while ignoring the
![]() $\ell _1$
-restriction formulated in Lemma 6.1. We build
$\ell _1$
-restriction formulated in Lemma 6.1. We build
![]() $\mathcal{B}_1$
from frequency vectors of solutions of the form
$\mathcal{B}_1$
from frequency vectors of solutions of the form
 \begin{align*} \left ({a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1}}\right ) + \sum _{i=0}^{\ell -1} a_i \cdot ((p-1){\mathbb{X}}^{i}) = 0. \end{align*}
\begin{align*} \left ({a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1}}\right ) + \sum _{i=0}^{\ell -1} a_i \cdot ((p-1){\mathbb{X}}^{i}) = 0. \end{align*}
That is, we take any element
![]() $a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1}$
from
$a_0 + a_1{\mathbb{X}} + \ldots + a_{\ell -1}{\mathbb{X}}^{\ell -1}$
from
![]() $\mathbb{F}_q^\ast$
and cancel it by a linear combination of elements from
$\mathbb{F}_q^\ast$
and cancel it by a linear combination of elements from
![]() $\{p-1, (p-1){\mathbb{X}}, \ldots, (p-1){\mathbb{X}}^{\ell -1}\} \subseteq \mathbb{F}_q^\ast$
. Formally, let
$\{p-1, (p-1){\mathbb{X}}, \ldots, (p-1){\mathbb{X}}^{\ell -1}\} \subseteq \mathbb{F}_q^\ast$
. Formally, let
![]() $e_1, \ldots, e_{q-1}$
denote the canonical basis of
$e_1, \ldots, e_{q-1}$
denote the canonical basis of
![]() $\mathbb{Z}^{q-1}$
. The set of statistics of all frequency vectors of the form described above then reads
$\mathbb{Z}^{q-1}$
. The set of statistics of all frequency vectors of the form described above then reads
 \begin{align*} \mathcal{B}_1 = \left \{{e_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})} + \sum _{i=0}^{\ell -1} a_i e_{f(-{\mathbb{X}}^{i})} \;:\; \sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast }\right \}. \end{align*}
\begin{align*} \mathcal{B}_1 = \left \{{e_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})} + \sum _{i=0}^{\ell -1} a_i e_{f(-{\mathbb{X}}^{i})} \;:\; \sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast }\right \}. \end{align*}
A moment of thought shows that
![]() $|\mathcal{B}_1| = q-1$
. Indeed, it is helpful to notice that for any
$|\mathcal{B}_1| = q-1$
. Indeed, it is helpful to notice that for any
![]() $h \in \mathbb{F}_q^\ast \setminus \{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}$
, there is exactly one element with a non-zero position in coordinate
$h \in \mathbb{F}_q^\ast \setminus \{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}$
, there is exactly one element with a non-zero position in coordinate
![]() $f(h)$
, and this coordinate is
$f(h)$
, and this coordinate is
![]() $1$
. That is, there is basically exactly one element in
$1$
. That is, there is basically exactly one element in
![]() $\mathcal{B}_1$
associated with each element of
$\mathcal{B}_1$
associated with each element of
![]() $\mathbb{F}_q^\ast$
. Generally, the elements of
$\mathbb{F}_q^\ast$
. Generally, the elements of
![]() $\mathcal{B}_1$
can be ordered to yield a lower triangular matrix
$\mathcal{B}_1$
can be ordered to yield a lower triangular matrix
![]() $M_q$
. To sketch this matrix, we first consider the case
$M_q$
. To sketch this matrix, we first consider the case
![]() $\ell =1$
. In this case, with our choice of indexing function
$\ell =1$
. In this case, with our choice of indexing function
![]() $f$
, the elements of
$f$
, the elements of
![]() ${\boldsymbol{B}}_1$
can be ordered to give the matrix displayed in Fig. 4. For the case of fields of prime order, this basis is already implicitly mentioned in [Reference Huang27].
${\boldsymbol{B}}_1$
can be ordered to give the matrix displayed in Fig. 4. For the case of fields of prime order, this basis is already implicitly mentioned in [Reference Huang27].

Figure 4. The matrix
![]() $M_p$
.
$M_p$
.
Note that this reduces to
![]() $M_2 = (2)$
in the case
$M_2 = (2)$
in the case
![]() $p=2$
. In this representation, rows are indexed by the field elements they represent, while columns are indexed by the field elements they are associated with. For
$p=2$
. In this representation, rows are indexed by the field elements they represent, while columns are indexed by the field elements they are associated with. For
![]() $\ell \geq 2$
, we can use the matrix
$\ell \geq 2$
, we can use the matrix
![]() $M_p$
for the compact representation of
$M_p$
for the compact representation of
![]() $M_q$
displayed in Fig. 5.
$M_q$
displayed in Fig. 5.

Figure 5. The matrix
![]() $M_q$
for
$M_q$
for
![]() $\ell \geq 2$
.
$\ell \geq 2$
.
In the matrix
![]() $M_q$
, the upper left block is an identity matrix of the appropriate dimension, the upper right is a zero matrix, the lower left is a matrix that only has non-zero entries in rows that correspond to
$M_q$
, the upper left block is an identity matrix of the appropriate dimension, the upper right is a zero matrix, the lower left is a matrix that only has non-zero entries in rows that correspond to
![]() $-1, \ldots, -{\mathbb{X}}^{\ell -1}$
while the lower right is a block diagonal matrix whose blocks are given by
$-1, \ldots, -{\mathbb{X}}^{\ell -1}$
while the lower right is a block diagonal matrix whose blocks are given by
![]() $M_p$
. In particular,
$M_p$
. In particular,
![]() $M_p$
is a lower triangular matrix. Because
$M_p$
is a lower triangular matrix. Because
![]() $M_p$
has determinant
$M_p$
has determinant
![]() $p$
the following is immediate.
$p$
the following is immediate.
Claim 6.3.
We have
![]() $ \det (M_q) = p^\ell = q.$
$ \det (M_q) = p^\ell = q.$
Let
![]() $\mathfrak{B}_1$
denote the
$\mathfrak{B}_1$
denote the
![]() $\mathbb{Z}$
-module generated by the elements of
$\mathbb{Z}$
-module generated by the elements of
![]() $\mathcal{B}_1$
. Then the lower triangular structure of
$\mathcal{B}_1$
. Then the lower triangular structure of
![]() $M_q$
also implies the following.
$M_q$
also implies the following.
Claim 6.4.
The rank of
![]() $\mathcal{B}_1$
is
$\mathcal{B}_1$
is
![]() $q-1$
.
$q-1$
.
The following lemma shows that the module
![]() $\mathfrak{M}$
is contained in
$\mathfrak{M}$
is contained in
![]() $\mathfrak{B}_1$
.
$\mathfrak{B}_1$
.
Lemma 6.5.
The
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{M}$
is contained in the
$\mathfrak{M}$
is contained in the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{B}_1$
.
$\mathfrak{B}_1$
.
Proof. We show that each element of
![]() $\mathfrak{M}$
can be written as a linear combination of elements of
$\mathfrak{M}$
can be written as a linear combination of elements of
![]() $\mathcal{B}_1$
. To this end it is sufficient to show that every frequency vector of a solution to an equation with exactly
$\mathcal{B}_1$
. To this end it is sufficient to show that every frequency vector of a solution to an equation with exactly
![]() $k_0$
non-zero entries and all-one coefficients can be written as a linear combination of the elements of
$k_0$
non-zero entries and all-one coefficients can be written as a linear combination of the elements of
![]() $\mathcal{B}_1$
. Let thus
$\mathcal{B}_1$
. Let thus
![]() $x \in \mathbb{N}^{q-1}$
be such a frequency vector, that is,
$x \in \mathbb{N}^{q-1}$
be such a frequency vector, that is,
![]() $\sum _{i=1}^{q-1} x_i f^{-1}(i) = 0$
in
$\sum _{i=1}^{q-1} x_i f^{-1}(i) = 0$
in
![]() $\mathbb{F}_q$
. Before we state a linear combination of
$\mathbb{F}_q$
. Before we state a linear combination of
![]() $x$
in terms of
$x$
in terms of
![]() $\mathcal{B}_1$
, observe that for each
$\mathcal{B}_1$
, observe that for each
![]() $j \in [q-1] \setminus \{q-1-(\ell -1)(p-1), q-1-(\ell -2)(p-1), \ldots, q-1\}$
, there is exactly one basis vector with a non-zero entry in position
$j \in [q-1] \setminus \{q-1-(\ell -1)(p-1), q-1-(\ell -2)(p-1), \ldots, q-1\}$
, there is exactly one basis vector with a non-zero entry in position
![]() $j$
. Moreover, the entry of this basis vector in position
$j$
. Moreover, the entry of this basis vector in position
![]() $j$
is
$j$
is
![]() $1$
. On the other hand, the basis vectors corresponding to the remaining
$1$
. On the other hand, the basis vectors corresponding to the remaining
![]() $\ell$
columns
$\ell$
columns
![]() $q-1-(\ell -1)(p-1), q-1-(\ell -2)(p-1), \ldots, q-1$
of
$q-1-(\ell -1)(p-1), q-1-(\ell -2)(p-1), \ldots, q-1$
of
![]() $M_q$
are actually integer multiples of the standard unit vectors, as
$M_q$
are actually integer multiples of the standard unit vectors, as
for
![]() $i=0, \ldots, \ell -1$
. With these observations, the only valid candidate for a linear combination of
$i=0, \ldots, \ell -1$
. With these observations, the only valid candidate for a linear combination of
![]() $x$
in terms of the elements of
$x$
in terms of the elements of
![]() $\mathcal{B}_1$
is given by
$\mathcal{B}_1$
is given by
 \begin{align*} x &= \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast \setminus \{-1,\ldots, -{\mathbb{X}}^{\ell -1}\}} x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})}\left ({e_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})} + \sum _{j=0}^{\ell -1} a_j e_{f(-{\mathbb{X}}^{j})} }\right )\\[5pt] & \qquad \qquad + \sum _{j=0}^{\ell -1}\frac{x_{f(-{\mathbb{X}}^{j})} - \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast \setminus \{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}} a_j x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})}}{p} \cdot pe_{f(-{\mathbb{X}}^{j})}. \end{align*}
\begin{align*} x &= \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast \setminus \{-1,\ldots, -{\mathbb{X}}^{\ell -1}\}} x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})}\left ({e_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})} + \sum _{j=0}^{\ell -1} a_j e_{f(-{\mathbb{X}}^{j})} }\right )\\[5pt] & \qquad \qquad + \sum _{j=0}^{\ell -1}\frac{x_{f(-{\mathbb{X}}^{j})} - \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast \setminus \{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}} a_j x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i})}}{p} \cdot pe_{f(-{\mathbb{X}}^{j})}. \end{align*}
It remains to argue why the coefficients of the basis vectors
![]() $pe_{f(-1)}, \ldots, pe_{f(-{\mathbb{X}}^{\ell -1})}$
in the second sum are integers. At this point, we will use that
$pe_{f(-1)}, \ldots, pe_{f(-{\mathbb{X}}^{\ell -1})}$
in the second sum are integers. At this point, we will use that
![]() $x$
is a solution statistic: Because
$x$
is a solution statistic: Because
 \begin{align*} \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast } x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} )} \sum _{j=0}^{\ell -1} a_j{\mathbb{X}}^{j} = 0 \qquad \text{in} \quad \mathbb{F}_q \end{align*}
\begin{align*} \sum _{\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^\ast } x_{f(\sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} )} \sum _{j=0}^{\ell -1} a_j{\mathbb{X}}^{j} = 0 \qquad \text{in} \quad \mathbb{F}_q \end{align*}
and the additive group
![]() $(\mathbb{F}_q,+)$
is isomorphic to
$(\mathbb{F}_q,+)$
is isomorphic to
![]() $((\mathbb{F}_p)^\ell, +)$
, all ‘components’ in the above sum must be zero and thus
$((\mathbb{F}_p)^\ell, +)$
, all ‘components’ in the above sum must be zero and thus
for all
![]() $j=0, \ldots, \ell -1$
. However, isolating the contribution from
$j=0, \ldots, \ell -1$
. However, isolating the contribution from
![]() $\{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}$
yields
$\{-1, \ldots, -{\mathbb{X}}^{\ell -1}\}$
yields
as the coefficient
![]() $a_j$
of
$a_j$
of
![]() ${\mathbb{X}}^{j}$
in
${\mathbb{X}}^{j}$
in
![]() $-{\mathbb{X}}^{i}$
is zero unless
$-{\mathbb{X}}^{i}$
is zero unless
![]() $i=j$
. Therefore, the right-hand side in (6.3) is divisible by
$i=j$
. Therefore, the right-hand side in (6.3) is divisible by
![]() $p$
and the claim follows.
$p$
and the claim follows.
6.1.2 Second basis
 $\mathcal{B}_2$
$\mathcal{B}_2$
In this subsection, we define a candidate set for the vectors
![]() $(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
in the statement of Lemma 6.1. That is, we define a set
$(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
in the statement of Lemma 6.1. That is, we define a set
![]() $\mathcal{B}_2$
all whose elements have non-negative components and
$\mathcal{B}_2$
all whose elements have non-negative components and
![]() $\ell _1$
-norm at most three. In other words, we are looking for solutions to
$\ell _1$
-norm at most three. In other words, we are looking for solutions to
with at most three different non-zero components.
Here again, our construction basically associates one basis vector to each element of
![]() $\mathbb{F}_q^\ast$
. However, due to the
$\mathbb{F}_q^\ast$
. However, due to the
![]() $\ell _1$
-restriction, there is less freedom in choosing the remaining non-zero coordinates. Our approach to design a set that satisfies this restriction while retaining a representation in a convenient block lower triangular matrix structure is to distinguish between elements of length one and of length at least two. We will therefore construct
$\ell _1$
-restriction, there is less freedom in choosing the remaining non-zero coordinates. Our approach to design a set that satisfies this restriction while retaining a representation in a convenient block lower triangular matrix structure is to distinguish between elements of length one and of length at least two. We will therefore construct
![]() $\mathcal{B}_2$
via two sets
$\mathcal{B}_2$
via two sets
![]() $\mathcal{B}^{(1)}$
and
$\mathcal{B}^{(1)}$
and
![]() $\mathcal{B}^{(\geq 2)}$
such that
$\mathcal{B}^{(\geq 2)}$
such that
![]() $\mathcal{B}_2$
is given as
$\mathcal{B}_2$
is given as
Let us start with an element
![]() $h = \sum _{i=0}^{\ell -1}a_i{\mathbb{X}}^{i}$
of length at least two in
$h = \sum _{i=0}^{\ell -1}a_i{\mathbb{X}}^{i}$
of length at least two in
![]() $\mathbb{F}_q$
. Assume that its leading coefficient is
$\mathbb{F}_q$
. Assume that its leading coefficient is
![]() $a_r$
for
$a_r$
for
![]() $r \in [\ell -1]$
. If a variable in (6.4) takes value
$r \in [\ell -1]$
. If a variable in (6.4) takes value
![]() $h$
, we may cancel its contribution to the equation by subtracting the two elements
$h$
, we may cancel its contribution to the equation by subtracting the two elements
![]() $a_r{\mathbb{X}}^r$
and
$a_r{\mathbb{X}}^r$
and
![]() $h - a_r{\mathbb{X}}^r$
, both of which are shorter than
$h - a_r{\mathbb{X}}^r$
, both of which are shorter than
![]() $h$
:
$h$
:
 \begin{align*} \sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} - a_r{\mathbb{X}}^r - \left ({\sum _{i=0}^{\ell -1}a_i{\mathbb{X}}^{i} - a_r{\mathbb{X}}^r}\right )=0. \end{align*}
\begin{align*} \sum _{i=0}^{\ell -1} a_i{\mathbb{X}}^{i} - a_r{\mathbb{X}}^r - \left ({\sum _{i=0}^{\ell -1}a_i{\mathbb{X}}^{i} - a_r{\mathbb{X}}^r}\right )=0. \end{align*}
This solution corresponds to the vector
This idea for field elements
![]() $h \in \mathbb{F}_q^{(\geq 2)}$
of length at least two then yields the
$h \in \mathbb{F}_q^{(\geq 2)}$
of length at least two then yields the
![]() $q-1-\ell (p-1)$
integer vectors
$q-1-\ell (p-1)$
integer vectors
 \begin{align*} \mathcal{B}^{(\geq 2)} = \left \{{e_{f(h)} + e_{f(-a_r{\mathbb{X}}^r)} + e_{f(-h+a_r{\mathbb{X}}^r)} \;:\; r \in [\ell -1] \text{ and } h = \sum _{i=0}^{r}a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^{(\geq 2)} \text{ with } a_r\not =0}\right \}. \end{align*}
\begin{align*} \mathcal{B}^{(\geq 2)} = \left \{{e_{f(h)} + e_{f(-a_r{\mathbb{X}}^r)} + e_{f(-h+a_r{\mathbb{X}}^r)} \;:\; r \in [\ell -1] \text{ and } h = \sum _{i=0}^{r}a_i{\mathbb{X}}^{i} \in \mathbb{F}_q^{(\geq 2)} \text{ with } a_r\not =0}\right \}. \end{align*}
For a field element
![]() $h$
of length one, an analogous shortening operation would correspond to the vector
$h$
of length one, an analogous shortening operation would correspond to the vector
If
![]() $p=2$
, this procedure applied to all field elements of length one yields
$p=2$
, this procedure applied to all field elements of length one yields
![]() $\ell$
distinct vectors and we are done. However, if
$\ell$
distinct vectors and we are done. However, if
![]() $p \gt 2$
, employing this idea for all elements of length one would only lead to
$p \gt 2$
, employing this idea for all elements of length one would only lead to
![]() $\ell (p-1)/2$
rather than
$\ell (p-1)/2$
rather than
![]() $\ell (p-1)$
additional vectors, as
$\ell (p-1)$
additional vectors, as
![]() $h$
and
$h$
and
![]() $-h$
are distinct and obviously give rise to the same statistic. As a consequence, for
$-h$
are distinct and obviously give rise to the same statistic. As a consequence, for
![]() $p\gt 2$
, we need to deviate from the above construction and come up with a modified ‘short-solution’ scheme. Let
$p\gt 2$
, we need to deviate from the above construction and come up with a modified ‘short-solution’ scheme. Let
![]() $h = a_r{\mathbb{X}}^r$
be an element of length one. If
$h = a_r{\mathbb{X}}^r$
be an element of length one. If
![]() $a_r \in \{1, \ldots (p-1)/2\}$
, we simply associate the vector
$a_r \in \{1, \ldots (p-1)/2\}$
, we simply associate the vector
![]() $e_{f(h)} + e_{f(-h)}$
to it, as indicated. If on the other hand
$e_{f(h)} + e_{f(-h)}$
to it, as indicated. If on the other hand
![]() $a_r \in \{(p+1)/2, \ldots, p-1\}$
, we let
$a_r \in \{(p+1)/2, \ldots, p-1\}$
, we let
![]() $h$
correspond to the vector
$h$
correspond to the vector
With this, for
![]() $p\gt 2$
, the part of
$p\gt 2$
, the part of
![]() $\mathcal{B}_2$
that corresponds to field elements of length one is given by the set
$\mathcal{B}_2$
that corresponds to field elements of length one is given by the set
 \begin{align} \mathcal{B}^{(1)}&= \bigcup _{r=0}^{\ell -1}\left (\left \{{e_{f(a_r{\mathbb{X}}^r)} + e_{f(-a_r{\mathbb{X}}^r)} \;:\; a_r \in [(p-1)/2]}\right \} \right.\nonumber \\[5pt] &\left.\quad \cup \left \{{e_{f(-a_r{\mathbb{X}}^r)} + e_{f(-{\mathbb{X}}^r)} + e_{f(a_r{\mathbb{X}}^r+{\mathbb{X}}^r)} \;:\; a_r \in [(p-1)/2]}\right \}\right ). \end{align}
\begin{align} \mathcal{B}^{(1)}&= \bigcup _{r=0}^{\ell -1}\left (\left \{{e_{f(a_r{\mathbb{X}}^r)} + e_{f(-a_r{\mathbb{X}}^r)} \;:\; a_r \in [(p-1)/2]}\right \} \right.\nonumber \\[5pt] &\left.\quad \cup \left \{{e_{f(-a_r{\mathbb{X}}^r)} + e_{f(-{\mathbb{X}}^r)} + e_{f(a_r{\mathbb{X}}^r+{\mathbb{X}}^r)} \;:\; a_r \in [(p-1)/2]}\right \}\right ). \end{align}
If
![]() $p=2$
, in line with the above discussion, we simply let
$p=2$
, in line with the above discussion, we simply let
 \begin{align} \mathcal{B}^{(1)}= \bigcup _{r=0}^{\ell -1}\left \{{2e_{f({\mathbb{X}}^r)} }\right \}. \end{align}
\begin{align} \mathcal{B}^{(1)}= \bigcup _{r=0}^{\ell -1}\left \{{2e_{f({\mathbb{X}}^r)} }\right \}. \end{align}
Again, a moment of thought shows that in any case,
![]() $|\mathcal{B}_2| = |\mathcal{B}_1| = q-1$
. Let
$|\mathcal{B}_2| = |\mathcal{B}_1| = q-1$
. Let
![]() $\mathfrak{B}_2$
denote the
$\mathfrak{B}_2$
denote the
![]() $\mathbb{Z}$
-module generated by the elements of
$\mathbb{Z}$
-module generated by the elements of
![]() $\mathcal{B}_2$
. Our choice of
$\mathcal{B}_2$
. Our choice of
![]() $\mathcal{B}_2$
has the advantage that again, its elements may be represented in a block lower triangular matrix. For this representation, it is instructive to consider the case
$\mathcal{B}_2$
has the advantage that again, its elements may be represented in a block lower triangular matrix. For this representation, it is instructive to consider the case
![]() $\ell =1$
first. In this case and with our choice of
$\ell =1$
first. In this case and with our choice of
![]() $f$
, the elements of
$f$
, the elements of
![]() $\mathcal{B}_2$
can be arranged as the columns of a matrix
$\mathcal{B}_2$
can be arranged as the columns of a matrix
![]() $A_p$
as in Fig. 6.
$A_p$
as in Fig. 6.

Figure 6. The matrix
![]() $A_p$
.
$A_p$
.
Here, as in the construction of
![]() $M_p$
, column
$M_p$
, column
![]() $i$
corresponds to the unique vector associated to
$i$
corresponds to the unique vector associated to
![]() $i \in \mathbb{F}_q$
. In the special case
$i \in \mathbb{F}_q$
. In the special case
![]() $p=2$
, this matrix reduces to
$p=2$
, this matrix reduces to
For
![]() $\ell \geq 2$
, the elements of
$\ell \geq 2$
, the elements of
![]() $\mathcal{B}_2$
may then be visualised in the matrix from Fig. 7.
$\mathcal{B}_2$
may then be visualised in the matrix from Fig. 7.

Figure 7. The matrix
![]() $A_q$
for
$A_q$
for
![]() $\ell \geq 2$
.
$\ell \geq 2$
.
In
![]() $A_q$
, column
$A_q$
, column
![]() $i \in [q-1]$
corresponds to the unique vector that is associated with the field element
$i \in [q-1]$
corresponds to the unique vector that is associated with the field element
![]() $f^{-1}(i)$
. Moreover, at this point, a moment of appreciation of our indexing choice
$f^{-1}(i)$
. Moreover, at this point, a moment of appreciation of our indexing choice
![]() $f$
is in place: Because
$f$
is in place: Because
![]() $f$
is monotonically decreasing with respect to length, there are no entries above the diagonal in the first
$f$
is monotonically decreasing with respect to length, there are no entries above the diagonal in the first
![]() $|\mathbb{F}_q^{(\geq 2)}|$
columns, as we only cancel field elements by strictly shorter ones. Moreover, the remaining
$|\mathbb{F}_q^{(\geq 2)}|$
columns, as we only cancel field elements by strictly shorter ones. Moreover, the remaining
![]() $\ell (p-1)$
columns are governed by a simple block structure. As a concrete example, (6.8) with
$\ell (p-1)$
columns are governed by a simple block structure. As a concrete example, (6.8) with
![]() $p=7$
reads
$p=7$
reads
 \begin{equation*} A_7 = \begin {pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\[5pt] 0 & 1 & 0 & 0 & 0 & 1\\[5pt] 0 & 0 & 1 & 0 & 1 & 0\\[5pt] 0 & 0 & 1 & 2 & 0 & 0\\[5pt] 0 & 1 & 0 & 0 & 1 & 0\\[5pt] 1 & 0 & 0 & 1 & 1 & 2 \end {pmatrix} \end{equation*}
\begin{equation*} A_7 = \begin {pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\[5pt] 0 & 1 & 0 & 0 & 0 & 1\\[5pt] 0 & 0 & 1 & 0 & 1 & 0\\[5pt] 0 & 0 & 1 & 2 & 0 & 0\\[5pt] 0 & 1 & 0 & 0 & 1 & 0\\[5pt] 1 & 0 & 0 & 1 & 1 & 2 \end {pmatrix} \end{equation*}
and
![]() $A_7$
would be used as a block matrix in any field of order
$A_7$
would be used as a block matrix in any field of order
![]() $7^\ell$
as shown in (6.9).
$7^\ell$
as shown in (6.9).
As each element of
![]() $\mathcal{B}_2$
corresponds to a solution with at most
$\mathcal{B}_2$
corresponds to a solution with at most
![]() $3 \leq k_0$
non-zero components, we obtain the following.
$3 \leq k_0$
non-zero components, we obtain the following.
Claim 6.6.
The
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{B}_2$
is contained in the
$\mathfrak{B}_2$
is contained in the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{M}$
.
$\mathfrak{M}$
.
Thus far we know
![]() $ \mathfrak{B}_2 \subseteq \mathfrak{M} \subseteq \mathfrak{B}_1.$
Moreover,
$ \mathfrak{B}_2 \subseteq \mathfrak{M} \subseteq \mathfrak{B}_1.$
Moreover,
![]() $\mathcal{B}_2$
has the desired
$\mathcal{B}_2$
has the desired
![]() $\ell _1$
-property. On the other hand, in comparison to
$\ell _1$
-property. On the other hand, in comparison to
![]() $\mathcal{B}_1$
, it is less clear that
$\mathcal{B}_1$
, it is less clear that
![]() $\mathcal{B}_2$
generates
$\mathcal{B}_2$
generates
![]() $\mathfrak{M}.$
It thus remains to show that in fact
$\mathfrak{M}.$
It thus remains to show that in fact
![]() $\mathfrak{B}_2 = \mathfrak{B}_1$
. We will do so by using the following fact, which is an immediate consequence of the adjugate matrix representation of the inverse matrix.
$\mathfrak{B}_2 = \mathfrak{B}_1$
. We will do so by using the following fact, which is an immediate consequence of the adjugate matrix representation of the inverse matrix.
Fact 6.7.
If
![]() $M$
is a free
$M$
is a free
![]() $\mathbb{Z}$
-module with basis
$\mathbb{Z}$
-module with basis
![]() $x_1, \ldots, x_n$
, a set of elements
$x_1, \ldots, x_n$
, a set of elements
![]() $y_1, \ldots, y_n\in M$
is a basis of
$y_1, \ldots, y_n\in M$
is a basis of
![]() $M$
if and only if the change of basis matrix
$M$
if and only if the change of basis matrix
![]() $(c_{ij})$
has determinant
$(c_{ij})$
has determinant
![]() $\pm 1$
.
$\pm 1$
.
We will apply Fact 6.7 to
![]() $M=\mathfrak{B}_1$
with
$M=\mathfrak{B}_1$
with
![]() $\{x_1, \ldots, x_n\} = \mathcal{B}_1$
and
$\{x_1, \ldots, x_n\} = \mathcal{B}_1$
and
![]() $\{y_1, \ldots, y_n\} = \mathcal{B}_2$
. Let
$\{y_1, \ldots, y_n\} = \mathcal{B}_2$
. Let
![]() $C_q \in \mathbb{Z}^{(q-1) \times (q-1)}$
be the matrix whose entries comprise the coefficients when we express the elements of
$C_q \in \mathbb{Z}^{(q-1) \times (q-1)}$
be the matrix whose entries comprise the coefficients when we express the elements of
![]() $\mathcal{B}_2$
by
$\mathcal{B}_2$
by
![]() $\mathcal{B}_1$
(recall that
$\mathcal{B}_1$
(recall that
![]() $\mathfrak{B}_2 \subseteq \mathfrak{B}_1$
) when we order the elements of
$\mathfrak{B}_2 \subseteq \mathfrak{B}_1$
) when we order the elements of
![]() $\mathcal{B}_1, \mathcal{B}_2$
as done in the construction of
$\mathcal{B}_1, \mathcal{B}_2$
as done in the construction of
![]() $M_q$
and
$M_q$
and
![]() $A_q$
. Thus
$A_q$
. Thus
![]() $A_q = M_q C_q.$
As
$A_q = M_q C_q.$
As
we do not need to compute
![]() $C_q$
explicitly to apply Fact 6.7, but instead it suffices to compute
$C_q$
explicitly to apply Fact 6.7, but instead it suffices to compute
![]() $\det (M_q)$
and
$\det (M_q)$
and
![]() $\det (A_q)$
. From Claim 6.3,
$\det (A_q)$
. From Claim 6.3,
![]() $\det (M_q)$
is already known. Moreover, for
$\det (M_q)$
is already known. Moreover, for
![]() $A_q$
, the computation will not be too hard, as
$A_q$
, the computation will not be too hard, as
![]() $A_q$
is a block lower triangular matrix. Therefore, we are just left to calculate the determinant of the non-trivial diagonal blocks.
$A_q$
is a block lower triangular matrix. Therefore, we are just left to calculate the determinant of the non-trivial diagonal blocks.
Lemma 6.8.
For any prime
![]() $p$
we have
$p$
we have
![]() $\det (A_p) = p.$
$\det (A_p) = p.$
Proof. The case
![]() $p=2$
is immediate. We thus assume that
$p=2$
is immediate. We thus assume that
![]() $p\gt 2$
in the following. We transform
$p\gt 2$
in the following. We transform
![]() $A_p$
into a lower triangular matrix by elementary column operations. To this end, let
$A_p$
into a lower triangular matrix by elementary column operations. To this end, let
![]() $a_1, \ldots, a_{q-1}$
be the columns of
$a_1, \ldots, a_{q-1}$
be the columns of
![]() $A_p$
. The first
$A_p$
. The first
![]() $(p+1)/2$
columns already have the right form, so we do not alter this part of the matrix. For any
$(p+1)/2$
columns already have the right form, so we do not alter this part of the matrix. For any
![]() $j=(p+3)/2, \ldots, p-1$
, subtract column
$j=(p+3)/2, \ldots, p-1$
, subtract column
![]() $a_{p+1-j}$
from column
$a_{p+1-j}$
from column
![]() $a_j$
. This yields the matrix
$a_j$
. This yields the matrix

Next, we swap column
![]() $(p+1)/2$
successively with columns
$(p+1)/2$
successively with columns
![]() $(p+3)/2, \ldots$
up to
$(p+3)/2, \ldots$
up to
![]() $p-1$
, yielding
$p-1$
, yielding

This changes the determinant by a factor of
![]() $(-1)^{(p-3)/2}$
. Finally, in order to erase the entry
$(-1)^{(p-3)/2}$
. Finally, in order to erase the entry
![]() $2$
in row
$2$
in row
![]() $(p+1)/2$
and column
$(p+1)/2$
and column
![]() $p-1$
, we add twice the sum of columns
$p-1$
, we add twice the sum of columns
![]() $(p+1)/2, \ldots, p-2$
to column
$(p+1)/2, \ldots, p-2$
to column
![]() $p-1$
. We thus obtain the matrix
$p-1$
. We thus obtain the matrix

with determinant
![]() $(-1)^{(p-3)/2}p$
. Multiplying with
$(-1)^{(p-3)/2}p$
. Multiplying with
![]() $(-1)^{(p-3)/2}$
from the column swaps yields the claim.
$(-1)^{(p-3)/2}$
from the column swaps yields the claim.
Corollary 6.9.
For any prime
![]() $p$
and
$p$
and
![]() $\ell \geq 1$
, we have
$\ell \geq 1$
, we have
![]() $ \det (A_q) = q.$
$ \det (A_q) = q.$
Finally, Claim 6.3 and Corollary 6.9 imply that
![]() $\det (C_q) = 1.$
Thus, by Fact 6.7,
$\det (C_q) = 1.$
Thus, by Fact 6.7,
![]() $\mathcal{B}_2$
is a basis of
$\mathcal{B}_2$
is a basis of
![]() $\mathfrak{B}_1$
, which implies that
$\mathfrak{B}_1$
, which implies that
![]() $ \mathfrak{B}_1 = \mathfrak{B}_2 = \mathfrak{M}.$
The column vectors
$ \mathfrak{B}_1 = \mathfrak{B}_2 = \mathfrak{M}.$
The column vectors
![]() $\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
of
$\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
of
![]() $A_q$
therefore enjoy the properties stated in Lemma 6.1.
$A_q$
therefore enjoy the properties stated in Lemma 6.1.
6.2 Proof of Lemma 6.2
Assume w.l.o.g. that
![]() $\chi _1=1$
. Moreover, by assumption, the set
$\chi _1=1$
. Moreover, by assumption, the set
![]() $\{\chi _1, \ldots, \chi _{k_0}\}$
contains at least two different elements, and so we may also assume that
$\{\chi _1, \ldots, \chi _{k_0}\}$
contains at least two different elements, and so we may also assume that
![]() $\chi _3 \not = 1$
(recall that
$\chi _3 \not = 1$
(recall that
![]() $k_0 \geq 3$
).
$k_0 \geq 3$
).
We define
![]() $(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
by distinguishing between three cases:
$(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
by distinguishing between three cases:
Case 1:
![]() $p=2$
and
$p=2$
and
![]() $\chi _2=1$
.
$\chi _2=1$
.
Denote the order of
![]() $\chi _3^{-1}$
in
$\chi _3^{-1}$
in
![]() $(\mathbb{F}_q^\ast, \cdot )$
by
$(\mathbb{F}_q^\ast, \cdot )$
by
![]() $\mathfrak{o}$
, so that the elements
$\mathfrak{o}$
, so that the elements
![]() $1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)}$
are pairwise distinct. Since
$1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)}$
are pairwise distinct. Since
![]() $p=2$
and
$p=2$
and
![]() $\mathfrak{o} \mid q-1$
,
$\mathfrak{o} \mid q-1$
,
![]() $\mathfrak{o}$
is an odd number. Moreover, because
$\mathfrak{o}$
is an odd number. Moreover, because
![]() $\chi _3^{-1} \not =1$
,
$\chi _3^{-1} \not =1$
,
![]() $\mathfrak{o} \geq 3$
. We now partition
$\mathfrak{o} \geq 3$
. We now partition
![]() $\mathbb{F}_q^\ast$
into orbits of the action of
$\mathbb{F}_q^\ast$
into orbits of the action of
![]() $(\{1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)} \}, \cdot )$
on
$(\{1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)} \}, \cdot )$
on
![]() $\mathbb{F}_q^\ast$
such that
$\mathbb{F}_q^\ast$
such that
where each orbit
![]() $\mathfrak{O}_j$
contains exactly
$\mathfrak{O}_j$
contains exactly
![]() $\mathfrak{o}$
elements. Suppose that
$\mathfrak{o}$
elements. Suppose that
![]() $\mathcal{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
$\mathcal{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
![]() $g_{i+1}^{(j)} = \chi _3^{-1}g_{i}^{(j)}$
.
$g_{i+1}^{(j)} = \chi _3^{-1}g_{i}^{(j)}$
.
To each
![]() $\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
$\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
![]() $j$
then yields the full set
$j$
then yields the full set
![]() $(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
$(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
![]() $\mathfrak{O}_j$
is defined as
$\mathfrak{O}_j$
is defined as
 \begin{align*} \mathcal{B}_j = \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{g_{2}^{(j)}+g_3^{(j)}}}\right \} . \end{align*}
\begin{align*} \mathcal{B}_j = \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{g_{2}^{(j)}+g_3^{(j)}}}\right \} . \end{align*}
In this definition, we have used that for
![]() $\chi _1 = -\chi _2=1$
and any
$\chi _1 = -\chi _2=1$
and any
![]() $h \in \mathbb{F}_q$
,
$h \in \mathbb{F}_q$
,
Note that the element
is non-zero and distinct from both
![]() $g_2^{(j)}$
and
$g_2^{(j)}$
and
![]() $g_3^{(j)}$
. It might be one of
$g_3^{(j)}$
. It might be one of
![]() $g_{1}^{(j)},g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
$g_{1}^{(j)},g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
We next argue that the union of the different
![]() $\mathcal{B}_j$
generates
$\mathcal{B}_j$
generates
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation and using that
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation and using that
![]() $\mathfrak{o}$
is odd,
$\mathfrak{o}$
is odd,
![]() $\mathcal{B}_j$
has the same span as
$\mathcal{B}_j$
has the same span as
Now, there are two cases.
-
1. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $g_2^{(j)}+g_3^{(j)} \in \{g_{1}^{(j)}, g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, either
$g_2^{(j)}+g_3^{(j)} \in \{g_{1}^{(j)}, g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, either
 $e_{g_2^{(j)}+g_3^{(j)}} =e_{g_{1}^{(j)}}$
, or we can subtract
$e_{g_2^{(j)}+g_3^{(j)}} =e_{g_{1}^{(j)}}$
, or we can subtract
 $e_{g_2^{(j)}+g_3^{(j)}}$
from or add it to the element
$e_{g_2^{(j)}+g_3^{(j)}}$
from or add it to the element
 $e_{g^{(j)}_1} \pm e_{g_2^{(j)}+g_3^{(j)}}$
to obtain
$e_{g^{(j)}_1} \pm e_{g_2^{(j)}+g_3^{(j)}}$
to obtain
 $e_{g_{1}^{(j)}}$
. After isolating
$e_{g_{1}^{(j)}}$
. After isolating
 $e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
$e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
 $\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
$\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
 $\mathfrak{O}_j$
. Thus, the union over all
$\mathfrak{O}_j$
. Thus, the union over all
 $\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
$\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
. -
2. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $g_2^{(j)}+g_3^{(j)} \notin \{g_1^{(j)}, g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, consider the union
$g_2^{(j)}+g_3^{(j)} \notin \{g_1^{(j)}, g_4^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, consider the union
 $\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each \begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} - e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{g_{1}^{(j)}+g_2^{(j)}}}\right \}. \end{align*}
\begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} - e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{g_{1}^{(j)}+g_2^{(j)}}}\right \}. \end{align*}
 $j$
, the element
$j$
, the element
 $g_1^{(j)}+g_2^{(j)}$
must be contained in some
$g_1^{(j)}+g_2^{(j)}$
must be contained in some
 $\mathfrak{O}_{j'}$
for
$\mathfrak{O}_{j'}$
for
 $j\not =j'$
, as in case (1),
$j\not =j'$
, as in case (1),
 $e_{g_{1}^{(j)}+g_2^{(j)}}$
can be used to isolate
$e_{g_{1}^{(j)}+g_2^{(j)}}$
can be used to isolate
 $e_{g_1^{(j')}}$
. After isolating
$e_{g_1^{(j')}}$
. After isolating
 $e_{g_1^{(j')}}$
for all
$e_{g_1^{(j')}}$
for all
 $j'$
, these elements can be straightforwardly used to linearly transform the union over all
$j'$
, these elements can be straightforwardly used to linearly transform the union over all
 $\mathcal{B}_j$
into the standard basis
$\mathcal{B}_j$
into the standard basis
 $(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
$(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
.
Finally, set
![]() $\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
Case 2:
![]() $p \not =2$
and
$p \not =2$
and
![]() $\chi _2=-1$
.
$\chi _2=-1$
.
We proceed almost exactly as before, only the choice of the ‘cyclic’ basis vectors is different:
Denote the order of
![]() $\chi _3^{-1}$
in
$\chi _3^{-1}$
in
![]() $(\mathbb{F}_q^\ast, \cdot )$
by
$(\mathbb{F}_q^\ast, \cdot )$
by
![]() $\mathfrak{o}$
, so that the elements
$\mathfrak{o}$
, so that the elements
![]() $1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)}$
are pairwise distinct. Then
$1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)}$
are pairwise distinct. Then
![]() $\mathfrak{o} \mid q-1$
, and since
$\mathfrak{o} \mid q-1$
, and since
![]() $\chi _3^{-1} \not =1$
,
$\chi _3^{-1} \not =1$
,
![]() $\mathfrak{o} \geq 2$
. We now partition
$\mathfrak{o} \geq 2$
. We now partition
![]() $\mathbb{F}_q^\ast$
into orbits of the action of
$\mathbb{F}_q^\ast$
into orbits of the action of
![]() $(\{1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)} \}, \cdot )$
on
$(\{1, \chi _3^{-1}, \ldots, \chi _3^{-(\mathfrak{o}-1)} \}, \cdot )$
on
![]() $\mathbb{F}_q^\ast$
such that
$\mathbb{F}_q^\ast$
such that
where each orbit
![]() $\mathfrak{O}_j$
contains exactly
$\mathfrak{O}_j$
contains exactly
![]() $\mathfrak{o}$
elements. Suppose that
$\mathfrak{o}$
elements. Suppose that
![]() $\mathfrak{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
$\mathfrak{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
![]() $g_{i+1}^{(j)} = \chi _3^{-1}g_{i}^{(j)}$
.
$g_{i+1}^{(j)} = \chi _3^{-1}g_{i}^{(j)}$
.
To each
![]() $\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
$\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
![]() $j$
then yields the full set
$j$
then yields the full set
![]() $(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
$(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
![]() $\mathfrak{O}_j$
is defined as
$\mathfrak{O}_j$
is defined as
 \begin{align*} \mathcal{B}_j = \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{2g_{1}^{(j)}}}\right \} . \end{align*}
\begin{align*} \mathcal{B}_j = \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{2g_{1}^{(j)}}}\right \} . \end{align*}
Here, we have used that for
![]() $\chi _1 = -\chi _2=1$
and
$\chi _1 = -\chi _2=1$
and
![]() $p \not =2$
,
$p \not =2$
,
Note that the element
![]() $2g_1^{(j)}$
is distinct from
$2g_1^{(j)}$
is distinct from
![]() $g_1^{(j)}$
. It might be one of
$g_1^{(j)}$
. It might be one of
![]() $g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
$g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
We next argue that the union of the different
![]() $\mathcal{B}_j$
generates
$\mathcal{B}_j$
generates
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation,
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation,
![]() $\mathcal{B}_j$
has the same span as
$\mathcal{B}_j$
has the same span as
Now, there are two cases.
-
1. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $2g_1^{(j)} \in \{g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. As in case 1, we can then subtract
$2g_1^{(j)} \in \{g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. As in case 1, we can then subtract
 $e_{2g_2^{(j)}}$
from or add it to
$e_{2g_2^{(j)}}$
from or add it to
 $e_{g_1^{(j)}} \pm e_{2g_2^{(j)}}$
to isolate
$e_{g_1^{(j)}} \pm e_{2g_2^{(j)}}$
to isolate
 $e_{g_1^{(j)}}$
. After isolating
$e_{g_1^{(j)}}$
. After isolating
 $e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
$e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
 $\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
$\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
 $\mathfrak{O}_j$
. Thus, the union over all
$\mathfrak{O}_j$
. Thus, the union over all
 $\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
$\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
. -
2. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $2g_1^{(j)} \notin \{g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, consider the union
$2g_1^{(j)} \notin \{g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}\}$
. In this case, consider the union
 $\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each \begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} \pm e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{2g_{1}^{(j)}}}\right \}. \end{align*}
\begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} \pm e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{2g_{1}^{(j)}}}\right \}. \end{align*}
 $j$
, the element
$j$
, the element
 $2g_1^{(j)}$
must be contained in some
$2g_1^{(j)}$
must be contained in some
 $\mathfrak{O}_{j'}$
for
$\mathfrak{O}_{j'}$
for
 $j\not =j'$
, as in case 1,
$j\not =j'$
, as in case 1,
 $e_{2g_{1}^{(j)}}$
can be used to isolate
$e_{2g_{1}^{(j)}}$
can be used to isolate
 $e_{g_1^{(j')}}$
. After isolating
$e_{g_1^{(j')}}$
. After isolating
 $e_{g_1^{(j')}}$
for all
$e_{g_1^{(j')}}$
for all
 $j'$
, these elements can be straightforwardly used to linearly transform the union over all
$j'$
, these elements can be straightforwardly used to linearly transform the union over all
 $\mathcal{B}_j$
into the standard basis
$\mathcal{B}_j$
into the standard basis
 $(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
$(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
.
In any case, set
![]() $\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
Case 3:
![]() $\chi _2\not = -1$
.
$\chi _2\not = -1$
.
Denote the order of
![]() $-\chi _2^{-1}$
in
$-\chi _2^{-1}$
in
![]() $(\mathbb{F}_q^\ast, \cdot )$
by
$(\mathbb{F}_q^\ast, \cdot )$
by
![]() $\mathfrak{o}$
, so that the elements
$\mathfrak{o}$
, so that the elements
![]() $1, -\chi _2^{-1}, \ldots, (-\chi _2^{-1})^{\mathfrak{o}-1}$
are pairwise distinct. Then
$1, -\chi _2^{-1}, \ldots, (-\chi _2^{-1})^{\mathfrak{o}-1}$
are pairwise distinct. Then
![]() $\mathfrak{o} \mid q-1$
, and since
$\mathfrak{o} \mid q-1$
, and since
![]() $-\chi _2^{-1} \not =1$
,
$-\chi _2^{-1} \not =1$
,
![]() $\mathfrak{o} \geq 2$
. We now partition
$\mathfrak{o} \geq 2$
. We now partition
![]() $\mathbb{F}_q^\ast$
into orbits of the action of
$\mathbb{F}_q^\ast$
into orbits of the action of
![]() $(\{1, -\chi _2^{-1}, \ldots,(-\chi _2^{-1})^{\mathfrak{o}-1} \}, \cdot )$
on
$(\{1, -\chi _2^{-1}, \ldots,(-\chi _2^{-1})^{\mathfrak{o}-1} \}, \cdot )$
on
![]() $\mathbb{F}_q^\ast$
such that
$\mathbb{F}_q^\ast$
such that
where each orbit
![]() $\mathfrak{O}_j$
contains exactly
$\mathfrak{O}_j$
contains exactly
![]() $\mathfrak{o}$
elements. Suppose that
$\mathfrak{o}$
elements. Suppose that
![]() $\mathfrak{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
$\mathfrak{O}_j=\{g^{(j)}_1, \ldots, g^{(j)}_{\mathfrak{o}}\}$
, where the elements are indexed such that
![]() $g_{i+1}^{(j)} = -\chi _2^{-1}g_{i}^{(j)}$
.
$g_{i+1}^{(j)} = -\chi _2^{-1}g_{i}^{(j)}$
.
To each
![]() $\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
$\mathfrak{O}_j$
, we associate a set of potential basis vectors whose union over different
![]() $j$
then yields the full set
$j$
then yields the full set
![]() $(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
$(\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1})$
. More precisely, the set corresponding to
![]() $\mathfrak{O}_j$
is defined as
$\mathfrak{O}_j$
is defined as
 \begin{align*} \mathcal{B}_j= \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{(1-\chi _3)g_{1}^{(j)}} }\right \}. \end{align*}
\begin{align*} \mathcal{B}_j= \bigcup _{i=1}^{\mathfrak{o}-1} \left \{{e_{g^{(j)}_i}+ e_{g^{(j)}_{i+1}}}\right \} \cup \left \{{e_{g_{1}^{(j)}} + e_{g_{2}^{(j)}} + e_{(1-\chi _3)g_{1}^{(j)}} }\right \}. \end{align*}
In the above, we have used that for
![]() $\chi _1=1$
,
$\chi _1=1$
,
Note that the element
![]() $(1-\chi _3)g_1^{(j)}$
is distinct from
$(1-\chi _3)g_1^{(j)}$
is distinct from
![]() $g_1^{(j)}$
. It might be one of
$g_1^{(j)}$
. It might be one of
![]() $g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
$g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
.
We next argue that the union of the different
![]() $\mathcal{B}_j$
generates
$\mathcal{B}_j$
generates
![]() $\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation,
$\mathbb{Z}^{\mathbb{F}_q^\ast }$
. By linear transformation,
![]() $\mathcal{B}_j$
has the same span as
$\mathcal{B}_j$
has the same span as
Now, there are two cases.
-
1. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $(1-\chi _3)g_{1}^{(j)}$
is one of the elements
$(1-\chi _3)g_{1}^{(j)}$
is one of the elements
 $g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
. As in case 1, we can then subtract
$g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
. As in case 1, we can then subtract
 $e_{(1-\chi _3)g_1^{(j)}}$
from or add it to
$e_{(1-\chi _3)g_1^{(j)}}$
from or add it to
 $e_{g_1^{(j)}} \pm e_{(1-\chi _3)g_1^{(j)}}$
to isolate
$e_{g_1^{(j)}} \pm e_{(1-\chi _3)g_1^{(j)}}$
to isolate
 $e_{g_1^{(j)}}$
. After isolating
$e_{g_1^{(j)}}$
. After isolating
 $e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
$e_{g_1^{(j)}}$
, a straightforward linear transformation yields a set of
 $\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
$\mathfrak{o}$
distinct unit vectors whose non-zero components are given by
 $\mathfrak{O}_j$
. Thus, the union over all
$\mathfrak{O}_j$
. Thus, the union over all
 $\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
$\mathcal{B}_j$
constitutes a set of linearly independent elements that generates
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
. -
2. For all
 $j \in [(q-1)/\mathfrak{o}]$
,
$j \in [(q-1)/\mathfrak{o}]$
,
 $(1-\chi _3)g_{1}^{(j)}$
is none of the elements
$(1-\chi _3)g_{1}^{(j)}$
is none of the elements
 $g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
. In this case, consider the union
$g_2^{(j)}, \ldots, g_{\mathfrak{o}}^{(j)}$
. In this case, consider the union
 $\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}}\mathcal{B}_j$
, which has the same span asSince for each \begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} \pm e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{(1-\chi _3)g_{1}^{(j)}}}\right \}. \end{align*}
\begin{align*} \bigcup _{j=1}^{(q-1)/\mathfrak{o}} \left \{{e_{g^{(j)}_1} + e_{g_2^{(j)}}, e_{g^{(j)}_1} - e_{g_3^{(j)}}, e_{g^{(j)}_1} + e_{g_4^{(j)}}, \ldots, e_{g^{(j)}_1} \pm e_{g_{\mathfrak{o}}^{(j)}}}\right \} \cup \left \{{e_{(1-\chi _3)g_{1}^{(j)}}}\right \}. \end{align*}
 $j$
, the element
$j$
, the element
 $(1-\chi _3)g_1^{(j)}$
must be contained in some
$(1-\chi _3)g_1^{(j)}$
must be contained in some
 $\mathfrak{O}_{j'}$
for
$\mathfrak{O}_{j'}$
for
 $j\not =j'$
, as in case (1),
$j\not =j'$
, as in case (1),
 $e_{(1-\chi _3)g_{1}^{(j)}}$
can be used to isolate
$e_{(1-\chi _3)g_{1}^{(j)}}$
can be used to isolate
 $e_{g_1^{(j')}}$
. After isolating
$e_{g_1^{(j')}}$
. After isolating
 $e_{g_1^{(j')}}$
for all
$e_{g_1^{(j')}}$
for all
 $j'$
, these elements can be straightforwardly used to linearly transform the union over all
$j'$
, these elements can be straightforwardly used to linearly transform the union over all
 $\mathcal{B}_j$
into the standard basis
$\mathcal{B}_j$
into the standard basis
 $(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
$(e_{h})_{h \in \mathbb{F}_q^\ast }$
of
 $\mathbb{Z}^{\mathbb{F}_q^*}$
.
$\mathbb{Z}^{\mathbb{F}_q^*}$
.
In any case, set
![]() $\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
$\bigcup _{j=1}^{(q-1)/\mathfrak{o}} \mathcal{B}_j = \{\mathfrak{b}_1, \ldots, \mathfrak{b}_{q-1}\}$
.
7. Proof of Proposition 2.6
7.1 Overview
Recall that Proposition 2.6 concerns the model
![]() $\underline{\mathbb{A}}$
with fixed numbers of non-zero entries per column and row, where both
$\underline{\mathbb{A}}$
with fixed numbers of non-zero entries per column and row, where both
![]() $m$
and the degree sequences
$m$
and the degree sequences
![]() $(d_i^{(n)})_{1 \leq i \leq n}$
and
$(d_i^{(n)})_{1 \leq i \leq n}$
and
![]() $(k_i^{(m)})_{1 \leq i \leq m}$
are specified. For the sake of readability, throughout this section, we will omit the superscript from
$(k_i^{(m)})_{1 \leq i \leq m}$
are specified. For the sake of readability, throughout this section, we will omit the superscript from
![]() $d_i^{(n)}$
and
$d_i^{(n)}$
and
![]() $k_i^{(m)}$
. Let
$k_i^{(m)}$
. Let
![]() $\mathfrak{A}$
be the
$\mathfrak{A}$
be the
![]() $\sigma$
-algebra generated by the numbers
$\sigma$
-algebra generated by the numbers
![]() ${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of equations of degree
${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )$
of equations of degree
![]() $\ell \geq 3$
with coefficients
$\ell \geq 3$
with coefficients
![]() $\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
. Let
$\chi _1,\ldots,\chi _\ell \in \mathbb{F}_q^*$
. Let
![]() $\Delta =\sum _{i=1}^n d_i$
denote the total degree. As before, we let
$\Delta =\sum _{i=1}^n d_i$
denote the total degree. As before, we let
![]() $\underline{\boldsymbol{A}}$
be the random matrix arising from the pairing model in this setting.
$\underline{\boldsymbol{A}}$
be the random matrix arising from the pairing model in this setting.
The aim in this section is to bound the expected size of the kernel of
![]() $\underline{\boldsymbol{A}}$
on
$\underline{\boldsymbol{A}}$
on
![]() $\mathfrak{O}$
from (2.7), that is,
$\mathfrak{O}$
from (2.7), that is,
![]() $|\ker \underline{\boldsymbol{A}}|\cdot {\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}$
. This is related to Proposition 2.6 through the identities
$|\ker \underline{\boldsymbol{A}}|\cdot {\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}$
. This is related to Proposition 2.6 through the identities
![]() ${\boldsymbol{Z}}^2 = {\boldsymbol{Z}} \cdot |\ker \underline{\boldsymbol{A}}|$
and
${\boldsymbol{Z}}^2 = {\boldsymbol{Z}} \cdot |\ker \underline{\boldsymbol{A}}|$
and
![]() $\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2 \cdot {\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}] = \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]\mathbb{E}_{\mathfrak{A}}[|\ker \underline{\boldsymbol{A}} |\cdot {\mathbb{1}}\{ \underline{\boldsymbol{A}} \in \mathfrak{O}\}]$
. Let us first observe that it suffices to count ‘nearly equitable’ kernel vectors, in the following sense. For a vector
$\mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}^2 \cdot {\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}] = \mathbb{E}_{\mathfrak{A}}[{\boldsymbol{Z}}]\mathbb{E}_{\mathfrak{A}}[|\ker \underline{\boldsymbol{A}} |\cdot {\mathbb{1}}\{ \underline{\boldsymbol{A}} \in \mathfrak{O}\}]$
. Let us first observe that it suffices to count ‘nearly equitable’ kernel vectors, in the following sense. For a vector
![]() $\sigma \in \mathbb{F}_q^n$
and
$\sigma \in \mathbb{F}_q^n$
and
![]() $s\in \mathbb{F}_q$
define the empirical frequency
$s\in \mathbb{F}_q$
define the empirical frequency
and let
![]() $\rho _\sigma =(\rho _\sigma (s))_{s\in \mathbb{F}_q}$
. If
$\rho _\sigma =(\rho _\sigma (s))_{s\in \mathbb{F}_q}$
. If
![]() $\mathfrak{O}$
occurs, then
$\mathfrak{O}$
occurs, then
![]() $\rho _\sigma$
is nearly uniform for most kernel vectors. Formally, we have the following statement.
$\rho _\sigma$
is nearly uniform for most kernel vectors. Formally, we have the following statement.
Fact 7.1.
For any
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $n$
large enough, we have
$n$
large enough, we have
![]() ${{\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}}\cdot |\ker \underline{\boldsymbol{A}}|\leq (1+\varepsilon )\left |{\left \{{\sigma \in \ker \underline{\boldsymbol{A}} \;:\; \|\rho _\sigma -q^{-1}\Delta {\mathbb{1}}\|_1\lt \varepsilon \Delta }\right \}}\right |.$
${{\mathbb{1}}\{\underline{\boldsymbol{A}} \in \mathfrak{O}\}}\cdot |\ker \underline{\boldsymbol{A}}|\leq (1+\varepsilon )\left |{\left \{{\sigma \in \ker \underline{\boldsymbol{A}} \;:\; \|\rho _\sigma -q^{-1}\Delta {\mathbb{1}}\|_1\lt \varepsilon \Delta }\right \}}\right |.$
Proof. Observe that to prove the claim, it is enough to show that for
![]() $\underline{\boldsymbol{A}} \in \mathfrak{O}$
, w.h.p. for all
$\underline{\boldsymbol{A}} \in \mathfrak{O}$
, w.h.p. for all
![]() $s \in \mathbb{F}_q$
,
$s \in \mathbb{F}_q$
,
![]() $\sum _{i=1}^n d_i{\mathbb{1}}\left \{{{\boldsymbol{x}}_{\underline{\boldsymbol{A}},i}=s}\right \} - \Delta/q \lt \varepsilon \Delta$
. Choose
$\sum _{i=1}^n d_i{\mathbb{1}}\left \{{{\boldsymbol{x}}_{\underline{\boldsymbol{A}},i}=s}\right \} - \Delta/q \lt \varepsilon \Delta$
. Choose
![]() $\delta =\delta (\varepsilon,q)\gt 0$
small enough. Thanks to condition (P1),
$\delta =\delta (\varepsilon,q)\gt 0$
small enough. Thanks to condition (P1),
![]() $\Delta = \sum _{i=1}^n d_i = \Omega (n)$
. Moreover, (P3) ensures that the sequence
$\Delta = \sum _{i=1}^n d_i = \Omega (n)$
. Moreover, (P3) ensures that the sequence
![]() $({\boldsymbol{d}}_n)_n$
is uniformly integrable, such that
$({\boldsymbol{d}}_n)_n$
is uniformly integrable, such that
for a large constant
![]() $d^*$
and all
$d^*$
and all
![]() $n$
large enough. On the other hand, for any degree
$n$
large enough. On the other hand, for any degree
![]() $\ell \leq d^*$
, a random vector
$\ell \leq d^*$
, a random vector
![]() ${\boldsymbol{x}}_{\underline{\boldsymbol{A}}}\in \ker \underline{\boldsymbol{A}}$
satisfies
${\boldsymbol{x}}_{\underline{\boldsymbol{A}}}\in \ker \underline{\boldsymbol{A}}$
satisfies
 \begin{align} \sum _{s,t\in \mathbb{F}_q}\sum _{i,j=1}^n{\mathbb{1}}\{d_i=d_j=\ell \}\left |{{\mathbb{P}}\left \lbrack{{\boldsymbol{x}}_{\underline{\boldsymbol{A}},i}=s,\ {\boldsymbol{x}}_{\underline{\boldsymbol{A}},j}=t\mid \underline{\boldsymbol{A}}}\right \rbrack -q^{-2}}\right |=o(n^2)\quad \mbox{for } \underline{\boldsymbol{A}}\in \mathfrak{O}. \end{align}
\begin{align} \sum _{s,t\in \mathbb{F}_q}\sum _{i,j=1}^n{\mathbb{1}}\{d_i=d_j=\ell \}\left |{{\mathbb{P}}\left \lbrack{{\boldsymbol{x}}_{\underline{\boldsymbol{A}},i}=s,\ {\boldsymbol{x}}_{\underline{\boldsymbol{A}},j}=t\mid \underline{\boldsymbol{A}}}\right \rbrack -q^{-2}}\right |=o(n^2)\quad \mbox{for } \underline{\boldsymbol{A}}\in \mathfrak{O}. \end{align}
Again by (P1), for all
![]() $\ell \in{\text{supp}}({\boldsymbol{d}})$
,
$\ell \in{\text{supp}}({\boldsymbol{d}})$
,
![]() $\sum _{j=1}^n{\mathbb{1}}\{d_j=\ell \}=\Omega (n)$
and consequently (7.3) shows that
$\sum _{j=1}^n{\mathbb{1}}\{d_j=\ell \}=\Omega (n)$
and consequently (7.3) shows that
Combining (7.2) and (7.4) with the definition (7.1) of
![]() $\rho _\sigma$
completes the proof.
$\rho _\sigma$
completes the proof.
We proceed to contemplate different regimes of ‘nearly equitable’ frequency vectors and employ increasingly subtle estimates to bound their contributions. To this end, let
![]() $\mathfrak{P}_q$
be the set of all possible frequency vectors, that is,
$\mathfrak{P}_q$
be the set of all possible frequency vectors, that is,
Moreover, for
![]() $\varepsilon \gt 0$
let
$\varepsilon \gt 0$
let
In addition, we introduce
 \begin{align*} \mathcal{Z}_\rho &=\left |{\left \{{\sigma \in \ker \underline{\boldsymbol{A}}\;:\;\rho _\sigma =\rho }\right \}}\right |&&(\rho \in \mathfrak{P}_q),\\[5pt] \mathcal{Z}_\varepsilon &= \sum _{\rho \in \mathfrak{P}_q(\varepsilon )}\mathcal{Z}_\rho &&(\varepsilon \geq 0),\\[5pt] \mathcal{Z}_{\varepsilon,\varepsilon '} &= \mathcal{Z}_{\varepsilon '}-\mathcal{Z}_\varepsilon &&(\varepsilon,\varepsilon '\geq 0). \end{align*}
\begin{align*} \mathcal{Z}_\rho &=\left |{\left \{{\sigma \in \ker \underline{\boldsymbol{A}}\;:\;\rho _\sigma =\rho }\right \}}\right |&&(\rho \in \mathfrak{P}_q),\\[5pt] \mathcal{Z}_\varepsilon &= \sum _{\rho \in \mathfrak{P}_q(\varepsilon )}\mathcal{Z}_\rho &&(\varepsilon \geq 0),\\[5pt] \mathcal{Z}_{\varepsilon,\varepsilon '} &= \mathcal{Z}_{\varepsilon '}-\mathcal{Z}_\varepsilon &&(\varepsilon,\varepsilon '\geq 0). \end{align*}
The following lemma sharpens the
![]() $\varepsilon \Delta$
error bound from Fact 7.1 to
$\varepsilon \Delta$
error bound from Fact 7.1 to
![]() $\omega n^{-1/2}\Delta$
.
$\omega n^{-1/2}\Delta$
.
Lemma 7.2.
For any small enough
![]() $\varepsilon \gt 0$
, for large enough
$\varepsilon \gt 0$
, for large enough
![]() $\omega =\omega (\varepsilon )\gt 1$
we have
$\omega =\omega (\varepsilon )\gt 1$
we have
![]() $\mathbb{E}_{\mathfrak{A}}\left \lbrack{\mathcal{Z}_{\omega n^{-1/2},\varepsilon }}\right \rbrack \lt \varepsilon q^{n-m}.$
$\mathbb{E}_{\mathfrak{A}}\left \lbrack{\mathcal{Z}_{\omega n^{-1/2},\varepsilon }}\right \rbrack \lt \varepsilon q^{n-m}.$
The proof of Lemma 7.2, which can be found in Section 7.2, is based on an expansion to the second order of the optimisation problem (2.5) around the equitable solution. Similar arguments have previously been applied in the theory of random constraint satisfaction problems, particularly random
![]() $k$
-XORSAT (e.g. [Reference Achlioptas, Naor and Peres4, Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Dubois and Mandler21]).
$k$
-XORSAT (e.g. [Reference Achlioptas, Naor and Peres4, Reference Ayre, Coja-Oghlan, Gao and Müller6, Reference Dubois and Mandler21]).
For
![]() $\rho$
that are within
$\rho$
that are within
![]() $O(n^{-1/2}\Delta )$
of the equitable solution such relatively routine arguments do not suffice anymore. Indeed, by comparison to examples of random CSPs that have been studied previously, sometimes by way of the small sub-graph conditioning technique, a new challenge arises. Namely, due to the algebraic nature of our problem the conceivable empirical distributions
$O(n^{-1/2}\Delta )$
of the equitable solution such relatively routine arguments do not suffice anymore. Indeed, by comparison to examples of random CSPs that have been studied previously, sometimes by way of the small sub-graph conditioning technique, a new challenge arises. Namely, due to the algebraic nature of our problem the conceivable empirical distributions
![]() $\rho _{{\boldsymbol{x}}}$
given that
$\rho _{{\boldsymbol{x}}}$
given that
![]() ${\boldsymbol{x}}\in \ker \underline{\boldsymbol{A}}$
are confined to a proper sub-lattice of
${\boldsymbol{x}}\in \ker \underline{\boldsymbol{A}}$
are confined to a proper sub-lattice of
![]() $\mathbb{Z}^q$
. The same is true of
$\mathbb{Z}^q$
. The same is true of
![]() $\mathfrak{P}_q$
unless
$\mathfrak{P}_q$
unless
![]() $\mathfrak{d}=1$
. Hence, we need to work out how these lattices intersect. Moreover, for
$\mathfrak{d}=1$
. Hence, we need to work out how these lattices intersect. Moreover, for
![]() $\rho \in \mathfrak{P}_q$
we need to calculate the number of assignments
$\rho \in \mathfrak{P}_q$
we need to calculate the number of assignments
![]() $\sigma$
such that
$\sigma$
such that
![]() $\rho _\sigma =\rho$
as well as the probability that such an assignment satisfies all equations. Seizing upon Proposition 2.5 and local limit theorem-type techniques, we will deal with these challenges in Section 7.3, where we prove the following.
$\rho _\sigma =\rho$
as well as the probability that such an assignment satisfies all equations. Seizing upon Proposition 2.5 and local limit theorem-type techniques, we will deal with these challenges in Section 7.3, where we prove the following.
Lemma 7.3.
Assume that
![]() $\mathfrak{d}$
and
$\mathfrak{d}$
and
![]() $q$
are coprime. Then for any
$q$
are coprime. Then for any
![]() $\varepsilon \gt 0$
for large enough
$\varepsilon \gt 0$
for large enough
![]() $\omega =\omega (\varepsilon )\gt 1$
we have
$\omega =\omega (\varepsilon )\gt 1$
we have
![]() $\mathbb{E}_{\mathfrak{A}}[\mathcal{Z}_{\omega n^{-1/2}}]\leq (1+\varepsilon )q^{n-m}$
w.h.p.
$\mathbb{E}_{\mathfrak{A}}[\mathcal{Z}_{\omega n^{-1/2}}]\leq (1+\varepsilon )q^{n-m}$
w.h.p.
7.2 Proof of Lemma 7.2
As we just saw, on the one hand we need to count
![]() $\sigma \in \mathbb{F}_q^n$
such that
$\sigma \in \mathbb{F}_q^n$
such that
![]() $\rho _\sigma$
hits a particular attainable
$\rho _\sigma$
hits a particular attainable
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
. On the other hand, we need to estimate the probability that such a given
$\rho \in \mathfrak{P}_q(\varepsilon )$
. On the other hand, we need to estimate the probability that such a given
![]() $\sigma$
satisfies all equations. The first of these, the entropy term, increases as
$\sigma$
satisfies all equations. The first of these, the entropy term, increases as
![]() $\rho$
becomes more equitable. The second, the probability term, takes greater values for non-uniform
$\rho$
becomes more equitable. The second, the probability term, takes greater values for non-uniform
![]() $\rho$
. Roughly, the more zero entries
$\rho$
. Roughly, the more zero entries
![]() $\rho$
contains, the better. The thrust of the proofs of Lemmas 7.2 and 7.3 is to show that the drop in entropy is an order of magnitude stronger than the boost to the success probability.
$\rho$
contains, the better. The thrust of the proofs of Lemmas 7.2 and 7.3 is to show that the drop in entropy is an order of magnitude stronger than the boost to the success probability.
Toward the proof of Lemma 7.2 we can get away with relatively rough bounds, mostly disregarding constant factors. The first claim bounds the entropy term. Instead of counting assignments we will take a probabilistic viewpoint. Hence, let
![]() $\boldsymbol{\sigma }\in \mathbb{F}_q^n$
be a uniformly random assignment.
$\boldsymbol{\sigma }\in \mathbb{F}_q^n$
be a uniformly random assignment.
Claim 7.4.
There exists
![]() $C\gt 0$
such that w.h.p.
$C\gt 0$
such that w.h.p.
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\|\rho _{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}}\|_1\gt t\sqrt{\Delta }}\right \rbrack \leq C\exp\!(-t^2/C)$
for all
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\|\rho _{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}}\|_1\gt t\sqrt{\Delta }}\right \rbrack \leq C\exp\!(-t^2/C)$
for all
![]() $t\geq 1$
.
$t\geq 1$
.
Proof. This is an immediate consequence of (P3) and Azuma–Hoeffding.
Let us move on to the probability term. We proceed indirectly by way of Bayes’ rule. Hence, fix
![]() $\rho \in \mathfrak{P}_q$
and let
$\rho \in \mathfrak{P}_q$
and let
![]() $\boldsymbol{\xi }=(\boldsymbol{\xi }_{ij})_{i,j\geq 1}$
be an infinite array of
$\boldsymbol{\xi }=(\boldsymbol{\xi }_{ij})_{i,j\geq 1}$
be an infinite array of
![]() $\mathbb{F}_q$
-valued random variables with distribution
$\mathbb{F}_q$
-valued random variables with distribution
![]() $\Delta ^{-1}\rho$
, mutually independent and independent of all other randomness. Moreover, let
$\Delta ^{-1}\rho$
, mutually independent and independent of all other randomness. Moreover, let
 \begin{align} \mathfrak{R}(\rho )&=\bigcap _{s\in \mathbb{F}_q}\left \{{\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}=\rho (s)}\right \},& \mathfrak{S}&=\left \{{\forall i \in [m]\;:\; \sum _{j=1}^{k_i}\boldsymbol{\chi }_{ij}\boldsymbol{\xi }_{ij}=0}\right \}. \end{align}
\begin{align} \mathfrak{R}(\rho )&=\bigcap _{s\in \mathbb{F}_q}\left \{{\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}=\rho (s)}\right \},& \mathfrak{S}&=\left \{{\forall i \in [m]\;:\; \sum _{j=1}^{k_i}\boldsymbol{\chi }_{ij}\boldsymbol{\xi }_{ij}=0}\right \}. \end{align}
In words,
![]() $\mathfrak{R}(\rho )$
is the event that the empirical distribution induced by the random vector
$\mathfrak{R}(\rho )$
is the event that the empirical distribution induced by the random vector
![]() $\boldsymbol{\xi }_{ij}$
, truncated at
$\boldsymbol{\xi }_{ij}$
, truncated at
![]() $i=m$
and
$i=m$
and
![]() $j=k_i$
for every
$j=k_i$
for every
![]() $i$
, works out to be
$i$
, works out to be
![]() $\rho \in \mathfrak{P}_q$
. Furthermore,
$\rho \in \mathfrak{P}_q$
. Furthermore,
![]() $\mathfrak{S}$
is the event that all
$\mathfrak{S}$
is the event that all
![]() $m$
checks are satisfied if we substitute the independent values
$m$
checks are satisfied if we substitute the independent values
![]() $\boldsymbol{\xi }_{ij}$
for the variables.
$\boldsymbol{\xi }_{ij}$
for the variables.
Crucially,
![]() $\mathfrak{S}$
ignores that the various equations share variables, or conversely that variables may appear in several distinct checks. Hence, the unconditional event
$\mathfrak{S}$
ignores that the various equations share variables, or conversely that variables may appear in several distinct checks. Hence, the unconditional event
![]() $\mathfrak{S}$
effectively just deals with a linear system whose Tanner graph consists of
$\mathfrak{S}$
effectively just deals with a linear system whose Tanner graph consists of
![]() $m$
checks with degrees
$m$
checks with degrees
![]() $k_1,\ldots,k_{m}$
and
$k_1,\ldots,k_{m}$
and
![]() $\sum _{i=1}^{m}k_i$
variable nodes of degree one each. However, the conditional probability
$\sum _{i=1}^{m}k_i$
variable nodes of degree one each. However, the conditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \mathfrak{R}(\rho )}\right \rbrack$
equals the probability that a random assignment
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \mathfrak{R}(\rho )}\right \rbrack$
equals the probability that a random assignment
![]() $\boldsymbol{\sigma }$
lies in the kernel of
$\boldsymbol{\sigma }$
lies in the kernel of
![]() $\underline{\boldsymbol{A}}$
given that
$\underline{\boldsymbol{A}}$
given that
![]() $\rho _{\boldsymbol{\sigma }}=\rho$
:
$\rho _{\boldsymbol{\sigma }}=\rho$
:
Claim 7.5.
With the previous notation, for any
![]() $\rho \in \mathfrak{P}_q$
,
$\rho \in \mathfrak{P}_q$
,
Proof. We relate both probabilities in (7.6) to the same random experiment. For this, let
![]() $\rho \in \mathfrak{P}_q$
be an empirical distribution that is compatible with the fixed vertex degrees, and additionally fix non-zero coefficients
$\rho \in \mathfrak{P}_q$
be an empirical distribution that is compatible with the fixed vertex degrees, and additionally fix non-zero coefficients
![]() $(\boldsymbol{\chi }_1, \ldots, \boldsymbol{\chi }_{k_\ell })$
for every equation. Thus, we consider the linear system as fixed.
$(\boldsymbol{\chi }_1, \ldots, \boldsymbol{\chi }_{k_\ell })$
for every equation. Thus, we consider the linear system as fixed.
We first take a look at the left hand side of (7.6): Conditionally on the empirical distribution of the variables
![]() $(\boldsymbol{\xi }_{11}, \ldots, \boldsymbol{\xi }_{1 k_1}, \boldsymbol{\xi }_{21}, \ldots, \boldsymbol{\xi }_{m k_{m}})$
being
$(\boldsymbol{\xi }_{11}, \ldots, \boldsymbol{\xi }_{1 k_1}, \boldsymbol{\xi }_{21}, \ldots, \boldsymbol{\xi }_{m k_{m}})$
being
![]() $\rho$
, by exchangeability, every possible assignment of values to the
$\rho$
, by exchangeability, every possible assignment of values to the
![]() $\Delta$
positions in the linear system has the same probability
$\Delta$
positions in the linear system has the same probability
![]() $\binom{\Delta }{\rho }^{-1}$
. The left hand side of (7.6) is thus equal to the number of all satisfying assignments with
$\binom{\Delta }{\rho }^{-1}$
. The left hand side of (7.6) is thus equal to the number of all satisfying assignments with
![]() $\rho (s)$
$\rho (s)$
![]() $s$
-entries for each
$s$
-entries for each
![]() $s \in \mathbb{F}_q$
divided by
$s \in \mathbb{F}_q$
divided by
![]() $\binom{\Delta }{\rho }$
.
$\binom{\Delta }{\rho }$
.
On the other hand, and turning to the right-hand side of (7.6), in the pairing model, variable clones are matched to check clones in a uniformly random manner. In such a uniform matching, for any fixed assignment
![]() $\sigma$
with empirical distribution
$\sigma$
with empirical distribution
![]() $\rho$
, the probability to end up with a specific assignment of values to the
$\rho$
, the probability to end up with a specific assignment of values to the
![]() $\Delta$
positions in the linear system has probability
$\Delta$
positions in the linear system has probability
![]() $\binom{\Delta }{\rho }^{-1}$
. The right-hand side of (7.6) is thus equal to the number of all satisfying assignments with
$\binom{\Delta }{\rho }^{-1}$
. The right-hand side of (7.6) is thus equal to the number of all satisfying assignments with
![]() $\rho (s)$
$\rho (s)$
![]() $s$
-entries for each
$s$
-entries for each
![]() $s \in \mathbb{F}_q$
, to positions in the fixed linear system, divided by
$s \in \mathbb{F}_q$
, to positions in the fixed linear system, divided by
![]() $\binom{\Delta }{\rho }$
.
$\binom{\Delta }{\rho }$
.
We are going to see momentarily that the unconditional probabilities of
![]() $\mathfrak{R}(\rho )$
and
$\mathfrak{R}(\rho )$
and
![]() $\mathfrak{S}$
are easy to calculate. In addition, we will be able to calculate the conditional probability
$\mathfrak{S}$
are easy to calculate. In addition, we will be able to calculate the conditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \mathfrak{R}(\rho )}\right \rbrack$
by way of the local limit theorem for sums of independent random variables. Finally, Lemma 7.2 will follow from these estimates via Bayes’ rule.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \mathfrak{R}(\rho )}\right \rbrack$
by way of the local limit theorem for sums of independent random variables. Finally, Lemma 7.2 will follow from these estimates via Bayes’ rule.
Claim 7.6.
For any
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $C=C(\varepsilon )\gt 0$
such that for all
$C=C(\varepsilon )\gt 0$
such that for all
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
,
$\rho \in \mathfrak{P}_q(\varepsilon )$
,
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}}\right \rbrack \leq q^{m(C\sum _{s\in \mathbb{F}_q}|\Delta ^{-1}\rho (s)-1/q|^3-1+\varepsilon ^3)}$
.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}}\right \rbrack \leq q^{m(C\sum _{s\in \mathbb{F}_q}|\Delta ^{-1}\rho (s)-1/q|^3-1+\varepsilon ^3)}$
.
Proof. For any
![]() $\rho \in \mathfrak{P}_q$
,
$\rho \in \mathfrak{P}_q$
,
![]() $h\geq 3$
and any
$h\geq 3$
and any
![]() $\chi _1,\ldots,\chi _h\in{\text{supp}}\boldsymbol{\chi }$
we aim to calculate
$\chi _1,\ldots,\chi _h\in{\text{supp}}\boldsymbol{\chi }$
we aim to calculate
 \begin{align*} P_h&=\log \sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0}\right \}\prod_{i=1}^h\frac{\rho (\sigma _i)}{\Delta }. \end{align*}
\begin{align*} P_h&=\log \sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0}\right \}\prod_{i=1}^h\frac{\rho (\sigma _i)}{\Delta }. \end{align*}
With this notation,
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}}\right \rbrack =\prod_{i=1}^m e^{P_{k_i}}$
. We regard
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}}\right \rbrack =\prod_{i=1}^m e^{P_{k_i}}$
. We regard
![]() $P_h$
as a function of the variables
$P_h$
as a function of the variables
![]() $(\rho (s))_{s \in \mathbb{F}_q}$
and will use Taylor’s theorem to expand it around the constant vector
$(\rho (s))_{s \in \mathbb{F}_q}$
and will use Taylor’s theorem to expand it around the constant vector
![]() $\bar \rho = q^{-1}\Delta {\mathbb{1}}$
:
$\bar \rho = q^{-1}\Delta {\mathbb{1}}$
:
for an appropriate error term
 \begin{align*} R_{\bar \rho,3}(\rho ) = \frac{1}{6}\sum _{s, s', s'' \in \mathbb{F}_q}\frac{\partial ^3 P_h}{\partial \rho (s)\partial \rho (s')\partial \rho (s'')}(z) \left ({\rho (s)-\frac{\Delta }{q}}\right ) \left ({\rho (s')-\frac{\Delta }{q}}\right )\left ({\rho (s'')-\frac{\Delta }{q}}\right ), \end{align*}
\begin{align*} R_{\bar \rho,3}(\rho ) = \frac{1}{6}\sum _{s, s', s'' \in \mathbb{F}_q}\frac{\partial ^3 P_h}{\partial \rho (s)\partial \rho (s')\partial \rho (s'')}(z) \left ({\rho (s)-\frac{\Delta }{q}}\right ) \left ({\rho (s')-\frac{\Delta }{q}}\right )\left ({\rho (s'')-\frac{\Delta }{q}}\right ), \end{align*}
where
![]() $z$
is some point
$z$
is some point
![]() $z$
on the segment from
$z$
on the segment from
![]() $\bar \rho$
to
$\bar \rho$
to
![]() $\rho$
. Firstly,
$\rho$
. Firstly,
![]() $P_h(\bar \rho ) = - \log q$
. The derivatives of
$P_h(\bar \rho ) = - \log q$
. The derivatives of
![]() $P_h$
work out to be
$P_h$
work out to be
 \begin{align*} \frac{\partial P_h}{\partial \rho (s)}&=\frac{\sum _{j=1}^h\sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0,\,\sigma _j=s}\right \}\prod_{i\neq j}\frac{\rho (\sigma _i)}{\Delta }}{\Delta \text{e}^{P_h}}\qquad (s\in \mathbb{F}_q),\\[5pt] \frac{\partial ^2 P_h}{\partial \rho (s)\partial \rho (s')}&=\frac{\sum _{j\not =j'}\sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0,\,\sigma _j=s,\sigma _{j'}=s'}\right \}\prod_{i\neq j,j'}\frac{\rho (\sigma _i)}{\Delta }}{\Delta ^2 \text{e}^{P_h}}\\[5pt] &\quad -\frac{\partial P_h}{\partial \rho (s)}\frac{\partial P_h}{\partial \rho (s')}\quad (s,s'\in \mathbb{F}_q). \end{align*}
\begin{align*} \frac{\partial P_h}{\partial \rho (s)}&=\frac{\sum _{j=1}^h\sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0,\,\sigma _j=s}\right \}\prod_{i\neq j}\frac{\rho (\sigma _i)}{\Delta }}{\Delta \text{e}^{P_h}}\qquad (s\in \mathbb{F}_q),\\[5pt] \frac{\partial ^2 P_h}{\partial \rho (s)\partial \rho (s')}&=\frac{\sum _{j\not =j'}\sum _{\sigma \in \mathbb{F}_q^h}{\mathbb{1}}\left \{{\sum _{i=1}^h\chi _i\sigma _i=0,\,\sigma _j=s,\sigma _{j'}=s'}\right \}\prod_{i\neq j,j'}\frac{\rho (\sigma _i)}{\Delta }}{\Delta ^2 \text{e}^{P_h}}\\[5pt] &\quad -\frac{\partial P_h}{\partial \rho (s)}\frac{\partial P_h}{\partial \rho (s')}\quad (s,s'\in \mathbb{F}_q). \end{align*}
Evaluating the derivatives at the equitable
![]() $\bar \rho =q^{-1}\Delta {\mathbb{1}}$
we obtain for any
$\bar \rho =q^{-1}\Delta {\mathbb{1}}$
we obtain for any
![]() $h\geq 3$
,
$h\geq 3$
,
 \begin{align*} \frac{\partial P_h}{\partial \rho (s)}\bigg |_{\bar \rho }&=\frac{hq^{-1}}{\Delta q^{-1}}=\frac{h}{\Delta },\\[5pt] \frac{\partial ^2 P_h}{\partial \rho (s)\partial \rho (s')}\bigg |_{\bar \rho }&=\frac{h(h-1)q^{-1}}{\Delta ^2 q^{-1}}-\frac{h^2}{\Delta ^2}=-\frac{h}{\Delta ^2},&&(s, s' \in \mathbb{F}_q). \end{align*}
\begin{align*} \frac{\partial P_h}{\partial \rho (s)}\bigg |_{\bar \rho }&=\frac{hq^{-1}}{\Delta q^{-1}}=\frac{h}{\Delta },\\[5pt] \frac{\partial ^2 P_h}{\partial \rho (s)\partial \rho (s')}\bigg |_{\bar \rho }&=\frac{h(h-1)q^{-1}}{\Delta ^2 q^{-1}}-\frac{h^2}{\Delta ^2}=-\frac{h}{\Delta ^2},&&(s, s' \in \mathbb{F}_q). \end{align*}
Hence, the Jacobi matrix and the Hessian work out to be
For all
![]() $h \leq h^\ast$
and
$h \leq h^\ast$
and
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
, the third partial derivatives are clearly uniformly bounded, that is, there is a constant
$\rho \in \mathfrak{P}_q(\varepsilon )$
, the third partial derivatives are clearly uniformly bounded, that is, there is a constant
![]() $C(\varepsilon, h^\ast )$
such that
$C(\varepsilon, h^\ast )$
such that
Finally, for any
![]() $\varepsilon \gt 0$
, because of assumptions (P1) and (P3), we can choose
$\varepsilon \gt 0$
, because of assumptions (P1) and (P3), we can choose
![]() $h^\ast$
large enough such that for
$h^\ast$
large enough such that for
![]() $n$
large enough, there are at most
$n$
large enough, there are at most
![]() $\varepsilon ^3 m$
equations with more than
$\varepsilon ^3 m$
equations with more than
![]() $h^\ast$
variables. For these, we trivially bound
$h^\ast$
variables. For these, we trivially bound
![]() $e^{P_h} \leq 1$
. For the remaining equations of uniformly bounded degree, we use the previously described approach based on the Taylor expansion: Since
$e^{P_h} \leq 1$
. For the remaining equations of uniformly bounded degree, we use the previously described approach based on the Taylor expansion: Since
![]() $\rho -\bar \rho \perp {\mathbb{1}}_q$
, (7.7), (7.8) and (7.9) imply the assertion.
$\rho -\bar \rho \perp {\mathbb{1}}_q$
, (7.7), (7.8) and (7.9) imply the assertion.
Claim 7.7.
For any
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $C=C(\varepsilon )\gt 0$
such that for all
$C=C(\varepsilon )\gt 0$
such that for all
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
,
$\rho \in \mathfrak{P}_q(\varepsilon )$
,
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack \geq C(\varepsilon ) \cdot n^{(1-q)/2}$
.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack \geq C(\varepsilon ) \cdot n^{(1-q)/2}$
.
Proof. Since the
![]() $\boldsymbol{\xi }_{ij}$
are mutually independent, the probability of
$\boldsymbol{\xi }_{ij}$
are mutually independent, the probability of
![]() $\mathfrak{R}(\rho )$
given
$\mathfrak{R}(\rho )$
given
![]() $\mathfrak{A}$
is nothing but
$\mathfrak{A}$
is nothing but
 \begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{(\rho (s))_{s\in \mathbb{F}_q}}\prod_{s\in \mathbb{F}_q}\left ({\frac{\rho (s)}{\Delta }}\right )^{\rho (s)}. \end{align*}
\begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{(\rho (s))_{s\in \mathbb{F}_q}}\prod_{s\in \mathbb{F}_q}\left ({\frac{\rho (s)}{\Delta }}\right )^{\rho (s)}. \end{align*}
The claim therefore follows from Stirling’s formula, together with assumption (P1).
Claim 7.8.
For all
![]() $\varepsilon \gt 0$
small enough and for all
$\varepsilon \gt 0$
small enough and for all
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
,
$\rho \in \mathfrak{P}_q(\varepsilon )$
,
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )\mid \mathfrak{S}}\right \rbrack = O(n^{(1-q)/2})$
.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )\mid \mathfrak{S}}\right \rbrack = O(n^{(1-q)/2})$
.
Proof. The claim follows from the local limit theorem for sums of independent random variables (e.g. [Reference Davis and McDonald18]). To elaborate, even once we condition on the event
![]() $\mathfrak{S}$
the random vectors
$\mathfrak{S}$
the random vectors
![]() $(\boldsymbol{\xi }_{ij})_{j\in [k_i]}$
,
$(\boldsymbol{\xi }_{ij})_{j\in [k_i]}$
,
![]() $1\leq i\leq m$
, remain independent for different
$1\leq i\leq m$
, remain independent for different
![]() $i\in [m]$
due to the independence of the
$i\in [m]$
due to the independence of the
![]() $(\boldsymbol{\xi }_{ij})_{i,j}$
. Indeed,
$(\boldsymbol{\xi }_{ij})_{i,j}$
. Indeed,
![]() $\mathfrak{S}$
only asks that each check be satisfied separately, without inducing dependencies among different checks. Thus, the vector
$\mathfrak{S}$
only asks that each check be satisfied separately, without inducing dependencies among different checks. Thus, the vector
 \begin{align*} \left ({\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}}\right )_{s\in \mathbb{F}_q}\qquad \mbox{given }\mathfrak{S} \end{align*}
\begin{align*} \left ({\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}}\right )_{s\in \mathbb{F}_q}\qquad \mbox{given }\mathfrak{S} \end{align*}
is a sum of
![]() $m$
independent random vectors. We first argue that
$m$
independent random vectors. We first argue that
![]() $(\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\})_{s\in \mathbb{F}_q^\ast }$
given
$(\sum _{i=1}^{m}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\})_{s\in \mathbb{F}_q^\ast }$
given
![]() $\mathfrak{S}$
satisfies a central limit theorem (note that we removed one coordinate from each vector). For this, let
$\mathfrak{S}$
satisfies a central limit theorem (note that we removed one coordinate from each vector). For this, let
![]() $\mathcal{C} \in{\mathbb{R}}^{\mathbb{F}_q^\ast \times \mathbb{F}_q^\ast }$
be defined by setting
$\mathcal{C} \in{\mathbb{R}}^{\mathbb{F}_q^\ast \times \mathbb{F}_q^\ast }$
be defined by setting
![]() $\mathcal{C}(s,s') = {\mathbb{1}}\{s=s'\}\frac{1}{q} - \frac{1}{q^2}$
. Then, thanks to the conditioning, for
$\mathcal{C}(s,s') = {\mathbb{1}}\{s=s'\}\frac{1}{q} - \frac{1}{q^2}$
. Then, thanks to the conditioning, for
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
, for all
$\rho \in \mathfrak{P}_q(\varepsilon )$
, for all
![]() $n, i$
, all entries of
$n, i$
, all entries of
![]() $C_i = \text{Cov}((\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\})_{s\in \mathbb{F}_q^\ast }|\mathfrak{S})$
will have distance at most
$C_i = \text{Cov}((\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\})_{s\in \mathbb{F}_q^\ast }|\mathfrak{S})$
will have distance at most
![]() $\delta$
from the corresponding entries of the matrix
$\delta$
from the corresponding entries of the matrix
![]() $k_i\cdot \mathcal{C}$
, where
$k_i\cdot \mathcal{C}$
, where
![]() $\delta = \delta (\varepsilon )$
and can be made arbitrarily small by choosing
$\delta = \delta (\varepsilon )$
and can be made arbitrarily small by choosing
![]() $\varepsilon$
smaller. In particular, for
$\varepsilon$
smaller. In particular, for
![]() $\varepsilon$
small enough, all covariance matrices
$\varepsilon$
small enough, all covariance matrices
![]() $C_i$
are positive definite.
$C_i$
are positive definite.
By the Lindeberg-Feller CLT, the standardised sequence
![]() $((\sum _{i=1}^m C_i)^{-1/2}\sum _{i=1}^{m}\sum _{j=1}^{k_i}({\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\} - \rho (s)/\Delta ))_{s\in \mathbb{F}_q^\ast }$
given
$((\sum _{i=1}^m C_i)^{-1/2}\sum _{i=1}^{m}\sum _{j=1}^{k_i}({\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\} - \rho (s)/\Delta ))_{s\in \mathbb{F}_q^\ast }$
given
![]() $\mathfrak{S}$
converges in distribution towards a multivariate standard Gaussian random variable if for every
$\mathfrak{S}$
converges in distribution towards a multivariate standard Gaussian random variable if for every
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
 \begin{align}& \sum _{i=1}^{m} \mathbb{E} \nonumber \\[5pt] &\left \lbrack{\left \|\left ({\sum _{i=1}^m C_i}\!\right )^{-1/2} \!\left ({\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} - \frac{k_i\rho (s)}{\Delta }}\!\right )_{s\in \mathbb{F}_q^\ast }\right \|_2^2{\mathbb{1}}\left \{{\left \|\left ({\sum _{i=1}^m C_i}\!\right )^{-1/2}\!\left ({\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} -\frac{k_i\rho (s)}{\Delta } }\!\right )_{s\in \mathbb{F}_q^\ast }\right \|_2\gt \delta }\right \}\Big \vert \mathfrak{S}\!}\right \rbrack \longrightarrow 0. \end{align}
\begin{align}& \sum _{i=1}^{m} \mathbb{E} \nonumber \\[5pt] &\left \lbrack{\left \|\left ({\sum _{i=1}^m C_i}\!\right )^{-1/2} \!\left ({\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} - \frac{k_i\rho (s)}{\Delta }}\!\right )_{s\in \mathbb{F}_q^\ast }\right \|_2^2{\mathbb{1}}\left \{{\left \|\left ({\sum _{i=1}^m C_i}\!\right )^{-1/2}\!\left ({\sum _{j=1}^{k_i}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} -\frac{k_i\rho (s)}{\Delta } }\!\right )_{s\in \mathbb{F}_q^\ast }\right \|_2\gt \delta }\right \}\Big \vert \mathfrak{S}\!}\right \rbrack \longrightarrow 0. \end{align}
To show (7.10), it is sufficient to show that for every
![]() $\delta '\gt 0$
,
$\delta '\gt 0$
,
However, since
![]() $m=\Theta (n)$
, this follows from the dominated convergence theorem via assumption (P3). Thus, the Lindeberg-Feller CLT applies. Moreover, since
$m=\Theta (n)$
, this follows from the dominated convergence theorem via assumption (P3). Thus, the Lindeberg-Feller CLT applies. Moreover, since
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
,
$\rho \in \mathfrak{P}_q(\varepsilon )$
,
![]() ${\mathbb{P}}\left ({\boldsymbol{\xi }_{ij}=s}\right ) \in (1/q-\varepsilon, 1/q+\varepsilon )$
for all
${\mathbb{P}}\left ({\boldsymbol{\xi }_{ij}=s}\right ) \in (1/q-\varepsilon, 1/q+\varepsilon )$
for all
![]() $s \in \mathbb{F}_q$
, so also the second condition of [Reference Davis and McDonald18, Theorem 2.1] is satisfied: The local limit theorem therefore implies that the probability of the most likely outcome of this random vector is of order
$s \in \mathbb{F}_q$
, so also the second condition of [Reference Davis and McDonald18, Theorem 2.1] is satisfied: The local limit theorem therefore implies that the probability of the most likely outcome of this random vector is of order
![]() $n^{(1-q)/2}$
; in symbols,
$n^{(1-q)/2}$
; in symbols,
The assertion is an immediate consequence of (7.11).
Proof of Lemma
7.2. Fix
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
such that
$\rho \in \mathfrak{P}_q(\varepsilon )$
such that
![]() $\omega \sqrt{\Delta }\leq \sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q|\lt \varepsilon \Delta$
. Combining Claims 7.6–7.8 with Bayes’ rule, we conclude that
$\omega \sqrt{\Delta }\leq \sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q|\lt \varepsilon \Delta$
. Combining Claims 7.6–7.8 with Bayes’ rule, we conclude that
Consequently, (7.6) and (7.12) imply that
Hence, combining Claim 7.4 with (7.13) and Lemma 7.17 and using the bound
![]() $\sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q|\lt \varepsilon \Delta$
, we obtain
$\sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q|\lt \varepsilon \Delta$
, we obtain
 \begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\boldsymbol{\sigma }\in \ker \underline{\boldsymbol{A}},\,\rho _{\boldsymbol{\sigma }}=\rho }\right \rbrack &=q^{m(\varepsilon ^3 + O(\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^3)-(\Omega (\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2)-1)+O(1)}\nonumber \\[5pt] & =q^{m(-1-\Omega (\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2)+O(1)}. \end{align}
\begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\boldsymbol{\sigma }\in \ker \underline{\boldsymbol{A}},\,\rho _{\boldsymbol{\sigma }}=\rho }\right \rbrack &=q^{m(\varepsilon ^3 + O(\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^3)-(\Omega (\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2)-1)+O(1)}\nonumber \\[5pt] & =q^{m(-1-\Omega (\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2)+O(1)}. \end{align}
Multiplying (7.14) with
![]() $q^n$
and summing on
$q^n$
and summing on
![]() $\rho \in \mathfrak{P}_q(\varepsilon )$
such that
$\rho \in \mathfrak{P}_q(\varepsilon )$
such that
![]() $\omega n^{-1/2} \Delta \leq \sum _{s\in \mathbb{F}_q}|\rho (s)- \Delta/q|$
, we finally obtain
$\omega n^{-1/2} \Delta \leq \sum _{s\in \mathbb{F}_q}|\rho (s)- \Delta/q|$
, we finally obtain
 \begin{align*}& \mathbb{E}_{\mathfrak{A}}\left \lbrack{\mathcal{Z}_{\omega n^{-1/2},\varepsilon }}\right \rbrack \\[5pt] & =q^{n-m+O(1)}\sum _{\substack{\rho \in \mathfrak{P}_q\\ \omega n^{-1/2} \Delta \leq \sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q| \lt \varepsilon \Delta }}\exp\!\left ({-\Omega \left ({n\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2}\right )}\right ) \lt \varepsilon q^{n-m}, \end{align*}
\begin{align*}& \mathbb{E}_{\mathfrak{A}}\left \lbrack{\mathcal{Z}_{\omega n^{-1/2},\varepsilon }}\right \rbrack \\[5pt] & =q^{n-m+O(1)}\sum _{\substack{\rho \in \mathfrak{P}_q\\ \omega n^{-1/2} \Delta \leq \sum _{s\in \mathbb{F}_q}|\rho (s)-\Delta/q| \lt \varepsilon \Delta }}\exp\!\left ({-\Omega \left ({n\sum _{s\in \mathbb{F}_q}|\rho (s)/\Delta -1/q|^2}\right )}\right ) \lt \varepsilon q^{n-m}, \end{align*}
provided
![]() $\omega =\omega (\varepsilon )\gt 0$
is chosen large enough.
$\omega =\omega (\varepsilon )\gt 0$
is chosen large enough.
7.3 Proof of Lemma 7.3
By comparison to the proof of Lemma 7.2, the main difference here is that we need to be more precise. Specifically, while in Claims 7.7 and 7.8 we got away with disregarding constant factors, here we need to be accurate up to a multiplicative
![]() $1+o(1)$
. Working out the probability term turns out to be delicate. As in Section 7.2, we introduce auxiliary
$1+o(1)$
. Working out the probability term turns out to be delicate. As in Section 7.2, we introduce auxiliary
![]() $\mathbb{F}_q$
-valued random variables
$\mathbb{F}_q$
-valued random variables
![]() $\boldsymbol{\xi }=(\boldsymbol{\xi }_{ij})_{i,j\geq 1}$
. These random variables are mutually independent as well as independent of all other randomness. But this time all
$\boldsymbol{\xi }=(\boldsymbol{\xi }_{ij})_{i,j\geq 1}$
. These random variables are mutually independent as well as independent of all other randomness. But this time all
![]() $\boldsymbol{\xi }_{ij}$
are uniform on
$\boldsymbol{\xi }_{ij}$
are uniform on
![]() $\mathbb{F}_q$
. Let
$\mathbb{F}_q$
. Let
![]() $\mathfrak{R}(\rho )$
and
$\mathfrak{R}(\rho )$
and
![]() $\mathfrak{S}$
be the events from (7.5).
$\mathfrak{S}$
be the events from (7.5).
Similarly as in Section 7.2 we will ultimately apply Bayes’ rule to compute the probability of
![]() $\mathfrak{S}$
given
$\mathfrak{S}$
given
![]() $\mathfrak{R}(\rho )$
and hence the conditional mean of
$\mathfrak{R}(\rho )$
and hence the conditional mean of
![]() $\mathcal{Z}_\rho$
. The individual probability of
$\mathcal{Z}_\rho$
. The individual probability of
![]() $\mathfrak{R}(\rho )$
is easy to compute.
$\mathfrak{R}(\rho )$
is easy to compute.
Claim 7.9.
For any
![]() $\rho \in \mathfrak{P}_q$
we have
$\rho \in \mathfrak{P}_q$
we have
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{\rho }q^{-\Delta }$
.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{\rho }q^{-\Delta }$
.
Proof. This is similar to the proof of Claim 7.7. As the
![]() $\boldsymbol{\xi }_{ij}$
are uniformly distributed and independent, we obtain
$\boldsymbol{\xi }_{ij}$
are uniformly distributed and independent, we obtain
 \begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{(\rho (s))_{s\in \mathbb{F}_q}}{\prod_{s\in \mathbb{F}_q}q^{-\rho (s)}}=\binom{\Delta }{\rho }q^{-\Delta }, \end{align*}
\begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{R}(\rho )}\right \rbrack =\binom{\Delta }{(\rho (s))_{s\in \mathbb{F}_q}}{\prod_{s\in \mathbb{F}_q}q^{-\rho (s)}}=\binom{\Delta }{\rho }q^{-\Delta }, \end{align*}
as claimed.
As a next step we calculate the conditional probability of
![]() $\mathfrak{S}$
given
$\mathfrak{S}$
given
![]() $\mathfrak{R}(\rho )$
. Similar to (7.1), for
$\mathfrak{R}(\rho )$
. Similar to (7.1), for
![]() $s\in \mathbb{F}_q$
define the empirical frequency
$s\in \mathbb{F}_q$
define the empirical frequency
 \begin{align} \boldsymbol{\rho }(s)=\sum _{i=1}^{ m}\sum _{j=1}^{ k_i} {\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} \end{align}
\begin{align} \boldsymbol{\rho }(s)=\sum _{i=1}^{ m}\sum _{j=1}^{ k_i} {\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \} \end{align}
and let
![]() $\boldsymbol{\rho }=(\boldsymbol{\rho }(s))_{s\in \mathbb{F}_q}$
as well as
$\boldsymbol{\rho }=(\boldsymbol{\rho }(s))_{s\in \mathbb{F}_q}$
as well as
![]() $\hat{\boldsymbol{\rho }}=(\boldsymbol{\rho }(s))_{s\in \mathbb{F}_q^{\ast }}$
. Of course, Proposition 2.5 implies that for some
$\hat{\boldsymbol{\rho }}=(\boldsymbol{\rho }(s))_{s\in \mathbb{F}_q^{\ast }}$
. Of course, Proposition 2.5 implies that for some
![]() $\rho \in \mathfrak{P}_q$
the event
$\rho \in \mathfrak{P}_q$
the event
![]() $\mathfrak{S}$
may be impossible given
$\mathfrak{S}$
may be impossible given
![]() $\mathfrak{R}(\rho )$
. Hence, to characterise the distributions
$\mathfrak{R}(\rho )$
. Hence, to characterise the distributions
![]() $\rho$
for which
$\rho$
for which
![]() $\mathfrak{S}$
can occur at all, we let
$\mathfrak{S}$
can occur at all, we let
Thus,
![]() $\mathfrak{L}$
contains all conceivable outcomes of truncated frequency vectors. Moreover,
$\mathfrak{L}$
contains all conceivable outcomes of truncated frequency vectors. Moreover,
![]() $\mathfrak{L}_0$
comprises those frequency vectors that can occur given
$\mathfrak{L}_0$
comprises those frequency vectors that can occur given
![]() $\mathfrak{S}$
, and
$\mathfrak{S}$
, and
![]() $\mathfrak{L}_*$
those that can result from random assignments
$\mathfrak{L}_*$
those that can result from random assignments
![]() $\boldsymbol{\sigma }$
to the variables. Hence,
$\boldsymbol{\sigma }$
to the variables. Hence,
![]() $\mathfrak{L}_0$
is a finite subset of the
$\mathfrak{L}_0$
is a finite subset of the
![]() $\mathbb{Z}$
-module generated by those sets
$\mathbb{Z}$
-module generated by those sets
![]() $\mathcal{S}_q(\chi _1,\ldots,\chi _\ell )$
from (2.15) with
$\mathcal{S}_q(\chi _1,\ldots,\chi _\ell )$
from (2.15) with
![]() ${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )\gt 0$
. The following lemma shows that actually the conditional probability
${\boldsymbol{m}}(\chi _1,\ldots,\chi _\ell )\gt 0$
. The following lemma shows that actually the conditional probability
![]() $\mathfrak{S}$
given
$\mathfrak{S}$
given
![]() $\mathfrak{R}(\rho )$
is asymptotically the same for all
$\mathfrak{R}(\rho )$
is asymptotically the same for all
![]() $\rho \in \mathfrak{L}_0$
, that is, for all conceivably satisfying
$\rho \in \mathfrak{L}_0$
, that is, for all conceivably satisfying
![]() $\rho$
that are nearly equitable.
$\rho$
that are nearly equitable.
Lemma 7.10.
W.h.p. uniformly for all
![]() $r \in \mathfrak{L}_0$
we have
$r \in \mathfrak{L}_0$
we have
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \hat{\boldsymbol{\rho }}=r}\right \rbrack \sim q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}-m}$
.
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{S}\mid \hat{\boldsymbol{\rho }}=r}\right \rbrack \sim q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}-m}$
.
We complement Lemma 7.10 by the following estimate of the probability that a uniformly random assignment
![]() $\boldsymbol{\sigma }\in \mathbb{F}_q^n$
hits the set
$\boldsymbol{\sigma }\in \mathbb{F}_q^n$
hits the set
![]() $\mathfrak{L}_0$
in the first place.
$\mathfrak{L}_0$
in the first place.
Lemma 7.11.
Assume that
![]() $\mathfrak{d}$
and
$\mathfrak{d}$
and
![]() $q$
are coprime. Then w.h.p.,
$q$
are coprime. Then w.h.p.,
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0}\right \rbrack \leq (1+o(1))q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}.$
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0}\right \rbrack \leq (1+o(1))q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}.$
We prove Lemmas 7.10 and 7.11 in Sections 7.4 and 7.5, respectively.
Proof of Lemma
7.3. Formula (7.6) extends to the present auxiliary probability space with uniformly distributed and independent
![]() $\boldsymbol{\xi }_{ij}$
(for precisely the same reasons given in Section 7.2). Hence, (7.6), (7.16) and (7.17) show that
$\boldsymbol{\xi }_{ij}$
(for precisely the same reasons given in Section 7.2). Hence, (7.6), (7.16) and (7.17) show that
Finally, combining (7.19) with Lemma 7.10 and Lemma 7.11, we obtain
 \begin{align*} \mathbb{E}_{\mathfrak{A}}[\mathcal{Z}_{\omega n^{-1/2}}]&\leq (1+o(1))q^{{\mathbb{1}}\left \{{|{\text{supp}}\boldsymbol{\chi }|=1}\right \}- m}\sum _{\sigma \in \mathbb{F}_q^n}{\mathbb{1}}\left \{{\hat{\rho }_\sigma \in \mathfrak{L}_0}\right \}\\[5pt] &=(1+o(1))q^{n-m+{\mathbb{1}}\left \{{|{\text{supp}}\boldsymbol{\chi }|=1}\right \}}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0}\right \rbrack \leq (1+o(1))q^{n-m}, \end{align*}
\begin{align*} \mathbb{E}_{\mathfrak{A}}[\mathcal{Z}_{\omega n^{-1/2}}]&\leq (1+o(1))q^{{\mathbb{1}}\left \{{|{\text{supp}}\boldsymbol{\chi }|=1}\right \}- m}\sum _{\sigma \in \mathbb{F}_q^n}{\mathbb{1}}\left \{{\hat{\rho }_\sigma \in \mathfrak{L}_0}\right \}\\[5pt] &=(1+o(1))q^{n-m+{\mathbb{1}}\left \{{|{\text{supp}}\boldsymbol{\chi }|=1}\right \}}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0}\right \rbrack \leq (1+o(1))q^{n-m}, \end{align*}
as desired.
7.4 Proof of Lemma 7.10
Given
![]() $\omega \gt 0$
(from (7.16)) we choose
$\omega \gt 0$
(from (7.16)) we choose
![]() $\varepsilon _0=\varepsilon _0(\omega,q)$
sufficiently small and let
$\varepsilon _0=\varepsilon _0(\omega,q)$
sufficiently small and let
![]() $0\lt \varepsilon \lt \varepsilon _0$
. Moreover, recall that the degree sequences
$0\lt \varepsilon \lt \varepsilon _0$
. Moreover, recall that the degree sequences
![]() $(d_1,\ldots,d_n)$
and
$(d_1,\ldots,d_n)$
and
![]() $(k_1,\ldots,k_m)$
satisfy properties (P1)-(P3). The proof hinges on a careful analysis of the conditional distribution of
$(k_1,\ldots,k_m)$
satisfy properties (P1)-(P3). The proof hinges on a careful analysis of the conditional distribution of
![]() $\hat{\boldsymbol{\rho }}$
given
$\hat{\boldsymbol{\rho }}$
given
![]() $\mathfrak{S}$
. We begin by observing that the vector
$\mathfrak{S}$
. We begin by observing that the vector
![]() $\hat{\boldsymbol{\rho }}$
is asymptotically normal given
$\hat{\boldsymbol{\rho }}$
is asymptotically normal given
![]() $\mathfrak{S}$
. Let
$\mathfrak{S}$
. Let
![]() ${\boldsymbol{I}}_{(q-1) \times (q-1)}$
the
${\boldsymbol{I}}_{(q-1) \times (q-1)}$
the
![]() $(q-1)\times (q-1)$
-identity matrix and let
$(q-1)\times (q-1)$
-identity matrix and let
![]() ${\boldsymbol{N}}\in{\mathbb{R}}^{\mathbb{F}_q^*}$
be a Gaussian vector with zero mean and covariance matrix
${\boldsymbol{N}}\in{\mathbb{R}}^{\mathbb{F}_q^*}$
be a Gaussian vector with zero mean and covariance matrix
Claim 7.12.
There exists a function
![]() $\alpha =\alpha (n,q)=o(1)$
such that for all axis-aligned cubes
$\alpha =\alpha (n,q)=o(1)$
such that for all axis-aligned cubes
![]() $U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
$U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
Proof. The conditional mean of
![]() $\hat{\boldsymbol{\rho }}$
given
$\hat{\boldsymbol{\rho }}$
given
![]() $\mathfrak{S}$
is uniform. To see this, consider any
$\mathfrak{S}$
is uniform. To see this, consider any
![]() $i\in [m]$
and
$i\in [m]$
and
![]() $h\in [k_i]$
. We claim that for any vector
$h\in [k_i]$
. We claim that for any vector
![]() $(\tau _j)_{j\in [k_i]\setminus \{h\}}$
,
$(\tau _j)_{j\in [k_i]\setminus \{h\}}$
,
Indeed, for any such vector
![]() $(\tau _j)_{j\in [k_i]\setminus \{h\}}$
there is exactly one value
$(\tau _j)_{j\in [k_i]\setminus \{h\}}$
there is exactly one value
![]() $\boldsymbol{\xi }_{ih}$
that will satisfy the equation, namely
$\boldsymbol{\xi }_{ih}$
that will satisfy the equation, namely
Hence, given
![]() $\mathfrak{S}$
the events
$\mathfrak{S}$
the events
![]() $\{\forall j\in [k_i]\setminus \{h\}\;:\;\boldsymbol{\xi }_{ij}=\tau _j\}$
are equally likely for all
$\{\forall j\in [k_i]\setminus \{h\}\;:\;\boldsymbol{\xi }_{ij}=\tau _j\}$
are equally likely for all
![]() $\tau$
, which implies (7.21). Furthermore, together with the definition (7.15) of
$\tau$
, which implies (7.21). Furthermore, together with the definition (7.15) of
![]() $\boldsymbol{\rho }$
, (7.21) readily implies that
$\boldsymbol{\rho }$
, (7.21) readily implies that
![]() ${\mathbb{E}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}|\mathfrak{S}}\right \rbrack }=q^{-1}\Delta {\mathbb{1}}$
. Similarly, (7.21) also shows that
${\mathbb{E}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}|\mathfrak{S}}\right \rbrack }=q^{-1}\Delta {\mathbb{1}}$
. Similarly, (7.21) also shows that
![]() $\Delta ^{-1/2}\hat{\boldsymbol{\rho }}$
has covariance matrix
$\Delta ^{-1/2}\hat{\boldsymbol{\rho }}$
has covariance matrix
![]() $\mathcal{C}$
given
$\mathcal{C}$
given
![]() $\mathfrak{S}$
.
$\mathfrak{S}$
.
Finally, we are left to prove the desired uniform convergence to the normal distribution. To this end we employ the multivariate Berry-Esseen theorem (e.g. [Reference Raič45]). Specifically, given a small
![]() $\alpha \gt 0$
choose
$\alpha \gt 0$
choose
![]() $K=K(q,\alpha )\gt 0$
and
$K=K(q,\alpha )\gt 0$
and
![]() $m_0=m_0(K)$
,
$m_0=m_0(K)$
,
![]() $n_0=n_0(K,m_0)$
sufficiently large. Assuming
$n_0=n_0(K,m_0)$
sufficiently large. Assuming
![]() $n\gt n_0$
, since
$n\gt n_0$
, since
![]() $m = \Theta (n)$
, we can ensure that
$m = \Theta (n)$
, we can ensure that
![]() $m\gt m_0$
. Also let
$m\gt m_0$
. Also let
 \begin{align*} k_i'&={\mathbb{1}}\{k_i\leq K\}k_i,&k_i''&=k_i-k_i',\\[5pt] \hat{\boldsymbol{\rho }}'(s)&=\sum _{1\leq i\leq m: k_i\leq K}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\},& \hat{\boldsymbol{\rho }}''(s)&=\sum _{1\leq i\leq m: k_i\gt K}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\},\\[5pt] \Delta '&=\sum _{i=1}^{m}k_i',&\Delta ''&=\sum _{i=1}^{m}k_i''. \end{align*}
\begin{align*} k_i'&={\mathbb{1}}\{k_i\leq K\}k_i,&k_i''&=k_i-k_i',\\[5pt] \hat{\boldsymbol{\rho }}'(s)&=\sum _{1\leq i\leq m: k_i\leq K}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\},& \hat{\boldsymbol{\rho }}''(s)&=\sum _{1\leq i\leq m: k_i\gt K}\sum _{j=1}^{k_i}{\mathbb{1}}\{\boldsymbol{\xi }_{ij}=s\},\\[5pt] \Delta '&=\sum _{i=1}^{m}k_i',&\Delta ''&=\sum _{i=1}^{m}k_i''. \end{align*}
Now again, assumption (P3) implies that the sequence
![]() $({\boldsymbol{k}}_n)_n$
is uniformly integrable, such that for large enough
$({\boldsymbol{k}}_n)_n$
is uniformly integrable, such that for large enough
![]() $n$
,
$n$
,
Moreover, by the same reasoning as in the previous paragraph the random vectors
![]() $\hat{\boldsymbol{\rho }}'$
and
$\hat{\boldsymbol{\rho }}'$
and
![]() $\hat{\boldsymbol{\rho }}''$
have means
$\hat{\boldsymbol{\rho }}''$
have means
![]() $q^{-1}\Delta '$
and
$q^{-1}\Delta '$
and
![]() $q^{-1}\Delta ''$
and covariances
$q^{-1}\Delta ''$
and covariances
![]() $\Delta '\mathcal{C}$
and
$\Delta '\mathcal{C}$
and
![]() $\Delta ''\mathcal{C}$
, respectively. Thus, (7.22) and Chebyshev’s inequality show that
$\Delta ''\mathcal{C}$
, respectively. Thus, (7.22) and Chebyshev’s inequality show that
Further, the Berry–Esseen theorem shows that
Here,
![]() $O(\!\cdot\!)$
refers to an
$O(\!\cdot\!)$
refers to an
![]() $n$
- and
$n$
- and
![]() $K$
-independent factor. Combining (7.24) and (7.23), we see that
$K$
-independent factor. Combining (7.24) and (7.23), we see that
The assertion follows from (7.25) by taking
![]() $\alpha \to 0$
slowly as
$\alpha \to 0$
slowly as
![]() $n\to \infty$
. For example, it is possible to choose
$n\to \infty$
. For example, it is possible to choose
![]() $\alpha = \log ^{-1} n$
and
$\alpha = \log ^{-1} n$
and
![]() $K=\Theta \left ({n^{1/4}}\right )$
thanks to assumption (P3).
$K=\Theta \left ({n^{1/4}}\right )$
thanks to assumption (P3).
The following claim states that the normal approximation from Claim 7.12 also holds for the unconditional random vector
![]() $\hat{\boldsymbol{\rho }}$
.
$\hat{\boldsymbol{\rho }}$
.
Claim 7.13.
There exists a function
![]() $\alpha =\alpha (n,q)=o(1)$
such that for all convex sets
$\alpha =\alpha (n,q)=o(1)$
such that for all convex sets
![]() $U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
$U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
Proof. This is an immediate consequence of Claim 7.9 and Stirling’s formula.
Let
![]() $k_0=\min{\text{supp}} ({\boldsymbol{k}})$
. In the case that
$k_0=\min{\text{supp}} ({\boldsymbol{k}})$
. In the case that
![]() $|{\text{supp}}\boldsymbol{\chi }|=1$
we set
$|{\text{supp}}\boldsymbol{\chi }|=1$
we set
![]() $\chi _1=\cdots =\chi _{k_0}$
to the single element of
$\chi _1=\cdots =\chi _{k_0}$
to the single element of
![]() ${\text{supp}}\boldsymbol{\chi }$
. Moreover, in the case that
${\text{supp}}\boldsymbol{\chi }$
. Moreover, in the case that
![]() $|{\text{supp}}\boldsymbol{\chi }|\gt 1$
we pick and fix any
$|{\text{supp}}\boldsymbol{\chi }|\gt 1$
we pick and fix any
![]() $\chi _1,\ldots,\chi _{k_0}\in{\text{supp}}\boldsymbol{\chi }$
such that
$\chi _1,\ldots,\chi _{k_0}\in{\text{supp}}\boldsymbol{\chi }$
such that
![]() $|\{\chi _1,\ldots,\chi _{k_0}\}|\gt 1$
. Let
$|\{\chi _1,\ldots,\chi _{k_0}\}|\gt 1$
. Let
![]() $\mathfrak{I}_0$
be the set of all
$\mathfrak{I}_0$
be the set of all
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $k_i=k_0$
and
$k_i=k_0$
and
![]() $\boldsymbol{\chi }_{ij}=\chi _j$
for
$\boldsymbol{\chi }_{ij}=\chi _j$
for
![]() $j=1,\ldots,k_0$
and let
$j=1,\ldots,k_0$
and let
![]() $\mathfrak{I}_1=[m]\setminus \mathfrak{I}_0$
. Then
$\mathfrak{I}_1=[m]\setminus \mathfrak{I}_0$
. Then
![]() $|\mathfrak{I}_0|=\Theta (n)$
w.h.p. Further, set
$|\mathfrak{I}_0|=\Theta (n)$
w.h.p. Further, set
Then
![]() $\hat{\boldsymbol{\rho }}={\boldsymbol{r}}_0+{\boldsymbol{r}}_1$
.
$\hat{\boldsymbol{\rho }}={\boldsymbol{r}}_0+{\boldsymbol{r}}_1$
.
Because the vectors
![]() $\boldsymbol{\xi }_i=(\boldsymbol{\xi }_{i,1},\ldots,\boldsymbol{\xi }_{i,k_i})$
are mutually independent, so are
$\boldsymbol{\xi }_i=(\boldsymbol{\xi }_{i,1},\ldots,\boldsymbol{\xi }_{i,k_i})$
are mutually independent, so are
![]() ${\boldsymbol{r}}_0=({\boldsymbol{r}}_0(s))_{s\in \mathbb{F}_q^*}$
and
${\boldsymbol{r}}_0=({\boldsymbol{r}}_0(s))_{s\in \mathbb{F}_q^*}$
and
![]() ${\boldsymbol{r}}_1=({\boldsymbol{r}}_1(s))_{s\in \mathbb{F}_q^*}$
. To analyse
${\boldsymbol{r}}_1=({\boldsymbol{r}}_1(s))_{s\in \mathbb{F}_q^*}$
. To analyse
![]() ${\boldsymbol{r}}_0$
precisely, let
${\boldsymbol{r}}_0$
precisely, let
 \begin{align*} \mathcal{S}_0&=\left \{{\sigma \in \mathbb{F}_q^{k_0}\;:\;\sum _{i=1}^{k_0}\chi _i\sigma _i=0}\right \}. \end{align*}
\begin{align*} \mathcal{S}_0&=\left \{{\sigma \in \mathbb{F}_q^{k_0}\;:\;\sum _{i=1}^{k_0}\chi _i\sigma _i=0}\right \}. \end{align*}
Moreover, for
![]() $\sigma \in \mathcal{S}_0$
let
$\sigma \in \mathcal{S}_0$
let
![]() ${\boldsymbol{R}}_\sigma$
be the number of indices
${\boldsymbol{R}}_\sigma$
be the number of indices
![]() $i\in \mathfrak{I}_0$
such that
$i\in \mathfrak{I}_0$
such that
![]() $\boldsymbol{\xi }_i=\sigma$
. Then conditionally on
$\boldsymbol{\xi }_i=\sigma$
. Then conditionally on
![]() $\mathfrak{S}$
, we have
$\mathfrak{S}$
, we have
 \begin{align*} {\boldsymbol{r}}_0(s)&=\sum _{i\in \mathfrak{I}_0}\sum _{j\in [k_i]}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}=\sum _{\sigma \in \mathcal{S}_0}\sum _{j=1}^{k_0}{\mathbb{1}}\left \{{\sigma _j=s}\right \}{\boldsymbol{R}}_\sigma \qquad \mbox{given }\mathfrak{S}, \end{align*}
\begin{align*} {\boldsymbol{r}}_0(s)&=\sum _{i\in \mathfrak{I}_0}\sum _{j\in [k_i]}{\mathbb{1}}\left \{{\boldsymbol{\xi }_{ij}=s}\right \}=\sum _{\sigma \in \mathcal{S}_0}\sum _{j=1}^{k_0}{\mathbb{1}}\left \{{\sigma _j=s}\right \}{\boldsymbol{R}}_\sigma \qquad \mbox{given }\mathfrak{S}, \end{align*}
which reduces our task to the investigation of
![]() ${\boldsymbol{R}}=({\boldsymbol{R}}_\sigma )_{\sigma \in \mathcal{S}_0}$
.
${\boldsymbol{R}}=({\boldsymbol{R}}_\sigma )_{\sigma \in \mathcal{S}_0}$
.
This is not too difficult because given
![]() $\mathfrak{S}$
the random vector
$\mathfrak{S}$
the random vector
![]() ${\boldsymbol{R}}$
has a multinomial distribution with parameter
${\boldsymbol{R}}$
has a multinomial distribution with parameter
![]() $|\mathfrak{I}_0|$
and uniform probabilities
$|\mathfrak{I}_0|$
and uniform probabilities
![]() $|\mathcal{S}_0|^{-1}$
. In effect, the individual entries
$|\mathcal{S}_0|^{-1}$
. In effect, the individual entries
![]() ${\boldsymbol{R}}(\sigma )$
,
${\boldsymbol{R}}(\sigma )$
,
![]() $\sigma \in \mathfrak{S}_0$
, will typically differ by only a few standard deviations, that is, their typical difference will be of order
$\sigma \in \mathfrak{S}_0$
, will typically differ by only a few standard deviations, that is, their typical difference will be of order
![]() $O(\sqrt{\Delta })$
. We require a precise quantitative version of this statement.
$O(\sqrt{\Delta })$
. We require a precise quantitative version of this statement.
Recalling the sets from (7.16) to (7.18), for
![]() $r_*\in \mathfrak{L}_0$
and
$r_*\in \mathfrak{L}_0$
and
![]() $0\lt \varepsilon \lt \varepsilon _0$
we let
$0\lt \varepsilon \lt \varepsilon _0$
we let
Furthermore, we say that
![]() ${\boldsymbol{R}}$
is
${\boldsymbol{R}}$
is
![]() $t$
-tame if
$t$
-tame if
![]() $|{\boldsymbol{R}}_\sigma -|\mathcal{S}_0|^{-1}|\mathfrak{I}_0||\leq t\sqrt{\Delta }$
for all
$|{\boldsymbol{R}}_\sigma -|\mathcal{S}_0|^{-1}|\mathfrak{I}_0||\leq t\sqrt{\Delta }$
for all
![]() $\sigma \in \mathcal{S}_0$
. Let
$\sigma \in \mathcal{S}_0$
. Let
![]() $\mathfrak{T}(t)$
be the event that
$\mathfrak{T}(t)$
be the event that
![]() ${\boldsymbol{R}}$
is
${\boldsymbol{R}}$
is
![]() $t$
-tame.
$t$
-tame.
Lemma 7.14.
W.h.p. for every
![]() $r_*\in \mathfrak{L}_0$
there exists
$r_*\in \mathfrak{L}_0$
there exists
![]() $r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
such that
$r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
such that
Proof. Recall that the event
![]() $\{{\hat{\boldsymbol{\rho }}}=r\}$
is the same as
$\{{\hat{\boldsymbol{\rho }}}=r\}$
is the same as
![]() $\mathfrak{R}(r')$
with
$\mathfrak{R}(r')$
with
![]() $r'(s)=r(s)$
for
$r'(s)=r(s)$
for
![]() $s\in \mathbb{F}_q^*$
and
$s\in \mathbb{F}_q^*$
and
![]() $r'(0) = \Delta -\| r\|_1$
. As a first step we observe that
$r'(0) = \Delta -\| r\|_1$
. As a first step we observe that
![]() ${\boldsymbol{R}}$
given
${\boldsymbol{R}}$
given
![]() $\mathfrak{S}$
is reasonably tame with a reasonably high probability. More precisely, since
$\mathfrak{S}$
is reasonably tame with a reasonably high probability. More precisely, since
![]() ${\boldsymbol{R}}$
has a multinomial distribution given
${\boldsymbol{R}}$
has a multinomial distribution given
![]() $\mathfrak{A}$
and
$\mathfrak{A}$
and
![]() $\mathfrak{S}$
, the Chernoff bound shows that w.h.p.
$\mathfrak{S}$
, the Chernoff bound shows that w.h.p.
Further, Claim 7.12 implies that
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack \geq \Omega _\varepsilon (\varepsilon ^{q-1})\geq \varepsilon ^q$
w.h.p., provided
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack \geq \Omega _\varepsilon (\varepsilon ^{q-1})\geq \varepsilon ^q$
w.h.p., provided
![]() $\varepsilon \lt \varepsilon _0=\varepsilon _0(\omega )$
is small enough. Combining this estimate with (7.27) and Bayes’ formula, we conclude that w.h.p. for every
$\varepsilon \lt \varepsilon _0=\varepsilon _0(\omega )$
is small enough. Combining this estimate with (7.27) and Bayes’ formula, we conclude that w.h.p. for every
![]() $r_*\in \mathfrak{L}_0$
,
$r_*\in \mathfrak{L}_0$
,
To complete the proof, assume that there does not exist
![]() $r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
that satisfies (7.26). Then for every
$r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
that satisfies (7.26). Then for every
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
we either have
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
we either have
Let
![]() $\mathfrak{X}_0$
be the set of all
$\mathfrak{X}_0$
be the set of all
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
for which (7.29) holds, and let
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
for which (7.29) holds, and let
![]() $\mathfrak{X}_1=\mathfrak{L}_0(r_*,\varepsilon )\setminus \mathfrak{X}_0$
. Then (7.29)–(7.30) yield
$\mathfrak{X}_1=\mathfrak{L}_0(r_*,\varepsilon )\setminus \mathfrak{X}_0$
. Then (7.29)–(7.30) yield
 \begin{align*} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \mathfrak{S},\ \hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack \\[5pt] &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_0\mid \mathfrak{S}}\right \rbrack +\sum _{r\in \mathfrak{X}_1}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \mathfrak{S},\,\hat{\boldsymbol{\rho }}=r}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack }\\[5pt] &\lt \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_0\mid \mathfrak{S}}\right \rbrack +(1-\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_1\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack } \lt 1-\varepsilon ^4, \end{align*}
\begin{align*} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \mathfrak{S},\ \hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack \\[5pt] &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_0\mid \mathfrak{S}}\right \rbrack +\sum _{r\in \mathfrak{X}_1}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \mathfrak{S},\,\hat{\boldsymbol{\rho }}=r}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack }\\[5pt] &\lt \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_0\mid \mathfrak{S}}\right \rbrack +(1-\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{X}_1\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r_*,\varepsilon )\mid \mathfrak{S}}\right \rbrack } \lt 1-\varepsilon ^4, \end{align*}
provided that
![]() $1-\varepsilon ^4\gt \frac{1}{2}$
, in contradiction to (7.28).
$1-\varepsilon ^4\gt \frac{1}{2}$
, in contradiction to (7.28).
Let
![]() $\mathfrak{M}=\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
and let
$\mathfrak{M}=\mathfrak{M}_q(\chi _1,\ldots,\chi _{k_0})$
and let
![]() $\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
be the basis of
$\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
be the basis of
![]() $\mathfrak{M}$
supplied by Proposition 2.5. Let us fix vectors
$\mathfrak{M}$
supplied by Proposition 2.5. Let us fix vectors
![]() $\tau ^{(1)},\ldots,\tau ^{(q-1)}\in \mathcal{S}_0$
whose frequency vectors as defined in (2.16) coincide with
$\tau ^{(1)},\ldots,\tau ^{(q-1)}\in \mathcal{S}_0$
whose frequency vectors as defined in (2.16) coincide with
![]() $\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
, that is,
$\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
, that is,
Also let
![]() $\mathfrak{T}(r,t)$
be the event that
$\mathfrak{T}(r,t)$
be the event that
![]() $\hat{\boldsymbol{\rho }}=r$
and that
$\hat{\boldsymbol{\rho }}=r$
and that
![]() ${\boldsymbol{R}}$
is
${\boldsymbol{R}}$
is
![]() $t$
-tame. The following lemma summarises the key step of the proof of Lemma 7.10.
$t$
-tame. The following lemma summarises the key step of the proof of Lemma 7.10.
Lemma 7.15.
W.h.p. for any
![]() $r_*\in \mathfrak{L}_0$
, any
$r_*\in \mathfrak{L}_0$
, any
![]() $1\leq t\leq \log n$
and any
$1\leq t\leq \log n$
and any
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
there exists a one-to-one map
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
there exists a one-to-one map
![]() $\psi \;:\;\mathfrak{T}(r,t)\to \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
such that for all
$\psi \;:\;\mathfrak{T}(r,t)\to \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
such that for all
![]() $(R,r_1)\in \mathfrak{T}(r,t)$
we have
$(R,r_1)\in \mathfrak{T}(r,t)$
we have
Proof. Since
![]() $r,r'\in \mathfrak{M}$
, we have
$r,r'\in \mathfrak{M}$
, we have
![]() $r-r'\in \mathfrak{M}$
w.h.p. Indeed, if
$r-r'\in \mathfrak{M}$
w.h.p. Indeed, if
![]() ${\text{supp}}\boldsymbol{\chi }\gt 1$
, then Proposition 2.5 shows that
${\text{supp}}\boldsymbol{\chi }\gt 1$
, then Proposition 2.5 shows that
![]() $\mathfrak{M}=\mathbb{Z}^{\mathbb{F}_q^*}$
w.h.p. Moreover, if
$\mathfrak{M}=\mathbb{Z}^{\mathbb{F}_q^*}$
w.h.p. Moreover, if
![]() ${\text{supp}}\boldsymbol{\chi }=1$
, then
${\text{supp}}\boldsymbol{\chi }=1$
, then
![]() $\mathfrak{M}$
is a proper subset of the integer lattice
$\mathfrak{M}$
is a proper subset of the integer lattice
![]() $\mathbb{Z}^{\mathbb{F}_q^*}$
. Nonetheless, Proposition 2.5 shows that the modules
$\mathbb{Z}^{\mathbb{F}_q^*}$
. Nonetheless, Proposition 2.5 shows that the modules
coincide for all
![]() $\ell \geq 3$
, and therefore
$\ell \geq 3$
, and therefore
![]() $\mathfrak{M}$
coincides with the
$\mathfrak{M}$
coincides with the
![]() $\mathbb{Z}$
-module generated by
$\mathbb{Z}$
-module generated by
![]() $\mathfrak{L}_0$
. Hence, in either case there is a unique representation
$\mathfrak{L}_0$
. Hence, in either case there is a unique representation
 \begin{align} {r'-r}&=\sum _{i=1}^{q-1}\lambda _i\mathfrak{b}_i&&(\lambda _i\in \mathbb{Z}) \end{align}
\begin{align} {r'-r}&=\sum _{i=1}^{q-1}\lambda _i\mathfrak{b}_i&&(\lambda _i\in \mathbb{Z}) \end{align}
in terms of the basis vectors. Because
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
and
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
and
 \begin{align*} \begin{pmatrix}\lambda _1\\[5pt] \vdots \\[5pt] \lambda _{q-1}\end{pmatrix}=\left ({\mathfrak{b}_1\ \cdots \ \mathfrak{b}_{q-1}}\right )^{-1}(r-r'), \end{align*}
\begin{align*} \begin{pmatrix}\lambda _1\\[5pt] \vdots \\[5pt] \lambda _{q-1}\end{pmatrix}=\left ({\mathfrak{b}_1\ \cdots \ \mathfrak{b}_{q-1}}\right )^{-1}(r-r'), \end{align*}
the coefficients satisfy
Now let
![]() $\lambda _0=-\sum _{i=1}^{q-1}\lambda _i$
, obtain the vector
$\lambda _0=-\sum _{i=1}^{q-1}\lambda _i$
, obtain the vector
![]() $R'$
from
$R'$
from
![]() $R$
by amending the entry
$R$
by amending the entry
![]() $R'_{\!\!0}$
corresponding to the zero solution
$R'_{\!\!0}$
corresponding to the zero solution
![]() $0\in \mathcal{S}_0$
to
$0\in \mathcal{S}_0$
to
 \begin{align*} R'_0 =R_0+\lambda _0,\qquad R_{\tau ^{(i)}}'=R_{\tau ^{(i)}}+\lambda _i \quad &\mbox{for all }i \in [q-1] \qquad \mbox{and} \qquad R_{\sigma }'=R_{\sigma } \\[5pt] &\mbox{for all }\sigma \not \in \{0,\tau ^{(1)},\ldots,\tau ^{(q-1)}\}. \end{align*}
\begin{align*} R'_0 =R_0+\lambda _0,\qquad R_{\tau ^{(i)}}'=R_{\tau ^{(i)}}+\lambda _i \quad &\mbox{for all }i \in [q-1] \qquad \mbox{and} \qquad R_{\sigma }'=R_{\sigma } \\[5pt] &\mbox{for all }\sigma \not \in \{0,\tau ^{(1)},\ldots,\tau ^{(q-1)}\}. \end{align*}
Further, define
![]() $\psi (R,r_1)=(R',r_1)$
. Then
$\psi (R,r_1)=(R',r_1)$
. Then
![]() ${\psi (R,r_1)}\in \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
due to (7.32) and (7.33). Moreover, Stirling’s formula and the mean value theorem show that
${\psi (R,r_1)}\in \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
due to (7.32) and (7.33). Moreover, Stirling’s formula and the mean value theorem show that
 \begin{align} \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{R}},{\boldsymbol{r}}_1)=(R,r_1)\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{R}},{\boldsymbol{r}}_1)=\psi (R,r_1)\mid \mathfrak{S}}\right \rbrack }&=\binom{|\mathfrak{I}_0|}{{R}}\binom{|\mathfrak{I}_0|}{{R'}}^{-1}=\exp\!\left \lbrack{\sum _{\sigma \in \mathcal{S}_0}O_\varepsilon \left ({R_\sigma \log R_\sigma -R'_\sigma \log R'_\sigma }\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}\left |{\int _{R'_\sigma/|\mathfrak{I}_0|}^{R_\sigma/|\mathfrak{I}_0|}\log z{\text{d}} z}\right |}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}\left ({\frac{R_\sigma }{|\mathfrak{I}_0|}-\frac{R'_\sigma }{|\mathfrak{I}_0|}}\right )\log \left ({\frac 1q+O_\varepsilon \left ({\frac{\omega +t}{\sqrt{\Delta }}}\right )}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}O_\varepsilon \left ({\frac{\omega +t}{\sqrt{\Delta }}\left ({\frac{R_\sigma }{|\mathfrak{I}_0|}-\frac{R'_\sigma }{|\mathfrak{I}_0|}}\right )}\right )}\right \rbrack . \end{align}
\begin{align} \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{R}},{\boldsymbol{r}}_1)=(R,r_1)\mid \mathfrak{S}}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{R}},{\boldsymbol{r}}_1)=\psi (R,r_1)\mid \mathfrak{S}}\right \rbrack }&=\binom{|\mathfrak{I}_0|}{{R}}\binom{|\mathfrak{I}_0|}{{R'}}^{-1}=\exp\!\left \lbrack{\sum _{\sigma \in \mathcal{S}_0}O_\varepsilon \left ({R_\sigma \log R_\sigma -R'_\sigma \log R'_\sigma }\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}\left |{\int _{R'_\sigma/|\mathfrak{I}_0|}^{R_\sigma/|\mathfrak{I}_0|}\log z{\text{d}} z}\right |}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}\left ({\frac{R_\sigma }{|\mathfrak{I}_0|}-\frac{R'_\sigma }{|\mathfrak{I}_0|}}\right )\log \left ({\frac 1q+O_\varepsilon \left ({\frac{\omega +t}{\sqrt{\Delta }}}\right )}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{O_\varepsilon (|\mathfrak{I}_0|)\sum _{\sigma \in \mathcal{S}_0}O_\varepsilon \left ({\frac{\omega +t}{\sqrt{\Delta }}\left ({\frac{R_\sigma }{|\mathfrak{I}_0|}-\frac{R'_\sigma }{|\mathfrak{I}_0|}}\right )}\right )}\right \rbrack . \end{align}
Since
![]() $|\mathfrak{I}_0|=\Theta _\varepsilon (\Delta )=\Theta _\varepsilon (n)$
w.h.p., (7.34) implies (7.31). Finally,
$|\mathfrak{I}_0|=\Theta _\varepsilon (\Delta )=\Theta _\varepsilon (n)$
w.h.p., (7.34) implies (7.31). Finally,
![]() $\psi$
is one to one because each vector has a unique representation with respect to the basis
$\psi$
is one to one because each vector has a unique representation with respect to the basis
![]() $(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
.
$(\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1})$
.
Roughly speaking, Lemma 7.15 shows that any two tame
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
close to a conceivable
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
close to a conceivable
![]() $r_*\in \mathfrak{L}_0$
are about equally likely. However, the map
$r_*\in \mathfrak{L}_0$
are about equally likely. However, the map
![]() $\psi$
produces solutions that are a little less tame than the ones we start from. The following corollary, which combines Lemmas 7.14 and 7.15, remedies this issue.
$\psi$
produces solutions that are a little less tame than the ones we start from. The following corollary, which combines Lemmas 7.14 and 7.15, remedies this issue.
Corollary 7.16.
W.h.p. for all
![]() $r_*\in \mathfrak{L}_0$
and all
$r_*\in \mathfrak{L}_0$
and all
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
we have
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
we have
Proof. Let
![]() $r^*$
be the vector supplied by Lemma 7.14. Applying Lemma 7.15 to
$r^*$
be the vector supplied by Lemma 7.14. Applying Lemma 7.15 to
![]() $r^*$
and
$r^*$
and
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
, we see that w.h.p.
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
, we see that w.h.p.
 \begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack &\geq \left ({1+O_\varepsilon \left ({\varepsilon \log \varepsilon }\right )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-\log \varepsilon )\mid \mathfrak{S}}\right \rbrack\nonumber \\[5pt] &\geq \frac 1{3|\mathfrak{L}_0(r_*,\varepsilon )|}\qquad \mbox{for all }r\in \mathfrak{L}_0(r_*,\varepsilon ). \end{align}
\begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack &\geq \left ({1+O_\varepsilon \left ({\varepsilon \log \varepsilon }\right )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-\log \varepsilon )\mid \mathfrak{S}}\right \rbrack\nonumber \\[5pt] &\geq \frac 1{3|\mathfrak{L}_0(r_*,\varepsilon )|}\qquad \mbox{for all }r\in \mathfrak{L}_0(r_*,\varepsilon ). \end{align}
In addition, we claim that w.h.p.
Indeed, applying Lemma 7.15 twice to
![]() $r$
and
$r$
and
![]() $r^*$
and invoking (7.26), we see that w.h.p.
$r^*$
and invoking (7.26), we see that w.h.p.
 \begin{align} \nonumber{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack &\geq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\mid \mathfrak{S}}\right \rbrack \nonumber \\[5pt] &\geq \left ({1-O_\varepsilon (\varepsilon \log \varepsilon )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r^*\mid \mathfrak{S}}\right \rbrack, \end{align}
\begin{align} \nonumber{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack &\geq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\mid \mathfrak{S}}\right \rbrack \nonumber \\[5pt] &\geq \left ({1-O_\varepsilon (\varepsilon \log \varepsilon )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r^*\mid \mathfrak{S}}\right \rbrack, \end{align}
 \begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-4\log \varepsilon )\setminus \mathfrak{T}(r,-3\log \varepsilon )\mid \mathfrak{S}}\right \rbrack \nonumber \\[5pt] &\leq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\setminus \mathfrak{T}(r^*,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack O_\varepsilon (\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r^*\mid \mathfrak{S}}\right \rbrack . \end{align}
\begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-4\log \varepsilon )\setminus \mathfrak{T}(r,-3\log \varepsilon )\mid \mathfrak{S}}\right \rbrack \nonumber \\[5pt] &\leq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\setminus \mathfrak{T}(r^*,-2\log \varepsilon )\mid \mathfrak{S}}\right \rbrack O_\varepsilon (\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r^*\mid \mathfrak{S}}\right \rbrack . \end{align}
Combining (7.37) and (7.38) yields (7.36).
Finally, (7.26), (7.35) and (7.36) show that w.h.p.
 \begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\boldsymbol{\rho }}=r,\,\mathfrak{S}}\right \rbrack \geq 1-\sqrt \varepsilon,\nonumber \\[5pt] &{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\boldsymbol{\rho }}=r',\,\mathfrak{S}}\right \rbrack \geq 1-\sqrt \varepsilon \qquad \mbox{for all }r,r'\in \mathfrak{L}_0(r_*,\varepsilon ), \end{align}
\begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\boldsymbol{\rho }}=r,\,\mathfrak{S}}\right \rbrack \geq 1-\sqrt \varepsilon,\nonumber \\[5pt] &{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\boldsymbol{\rho }}=r',\,\mathfrak{S}}\right \rbrack \geq 1-\sqrt \varepsilon \qquad \mbox{for all }r,r'\in \mathfrak{L}_0(r_*,\varepsilon ), \end{align}
Proof of Lemma
7.10. We are going to show that the conditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack$
of hitting some particular
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack$
of hitting some particular
![]() $r\in \mathfrak{L}_0$
coincides with the unconditional probability
$r\in \mathfrak{L}_0$
coincides with the unconditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r}\right \rbrack$
up to a factor of
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r}\right \rbrack$
up to a factor of
![]() $(1+o_\varepsilon (1)) q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}$
. Then the assertion follows from Bayes’ formula.
$(1+o_\varepsilon (1)) q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}$
. Then the assertion follows from Bayes’ formula.
The unconditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r}\right \rbrack$
is given precisely by Claim 7.9. Hence, recalling the
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r}\right \rbrack$
is given precisely by Claim 7.9. Hence, recalling the
![]() $(q-1)\times (q-1)$
-matrix
$(q-1)\times (q-1)$
-matrix
![]() $\mathcal{C}=q^{-1}{\boldsymbol{I}}_{(q-1) \times (q-1)}-q^{-2}{\mathbb{1}}_{(q-1)\times (q-1)}$
from (7.20) and applying Stirling’s formula, we obtain
$\mathcal{C}=q^{-1}{\boldsymbol{I}}_{(q-1) \times (q-1)}-q^{-2}{\mathbb{1}}_{(q-1)\times (q-1)}$
from (7.20) and applying Stirling’s formula, we obtain
w.h.p.
Next we will show that the conditional probability
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack$
works out to be asymptotically the same, up to an additional factor of
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\boldsymbol{\rho }}=r\mid \mathfrak{S}}\right \rbrack$
works out to be asymptotically the same, up to an additional factor of
![]() $q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}$
. Indeed, Claim 7.12 shows that for any
$q^{{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}$
. Indeed, Claim 7.12 shows that for any
![]() $r\in \mathfrak{L}_0$
the conditional probability that
$r\in \mathfrak{L}_0$
the conditional probability that
![]() $\hat{\boldsymbol{\rho }}$
hits the set
$\hat{\boldsymbol{\rho }}$
hits the set
![]() $\mathfrak{L}_0(r,\varepsilon )$
is asymptotically equal to the probability of the event
$\mathfrak{L}_0(r,\varepsilon )$
is asymptotically equal to the probability of the event
![]() $\{\|{\boldsymbol{N}}-\Delta ^{-1/2}(r-q^{-1}\Delta {\mathbb{1}})\|_\infty \lt \varepsilon \}$
. Moreover, Corollary 7.16 implies that given
$\{\|{\boldsymbol{N}}-\Delta ^{-1/2}(r-q^{-1}\Delta {\mathbb{1}})\|_\infty \lt \varepsilon \}$
. Moreover, Corollary 7.16 implies that given
![]() $\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r,\varepsilon )$
,
$\hat{\boldsymbol{\rho }}\in \mathfrak{L}_0(r,\varepsilon )$
,
![]() $\hat{\boldsymbol{\rho }}$
is within
$\hat{\boldsymbol{\rho }}$
is within
![]() $o_\varepsilon (1)$
of the uniform distribution on
$o_\varepsilon (1)$
of the uniform distribution on
![]() $\mathfrak{L}_0(r,\varepsilon )$
. Furthermore, Lemma 3.6 and Proposition 2.5 show that the number of points in
$\mathfrak{L}_0(r,\varepsilon )$
. Furthermore, Lemma 3.6 and Proposition 2.5 show that the number of points in
![]() $\mathfrak{L}_0(r,\varepsilon )$
satisfies
$\mathfrak{L}_0(r,\varepsilon )$
satisfies
 \begin{align*} \frac{|\mathfrak{L}_0(r,\varepsilon )|}{\left |{\left \{{z\in \mathbb{Z}^{q-1}\;:\;\|z-r\|_\infty \leq \varepsilon \sqrt{\Delta }}\right \}}\right |}\sim q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}. \end{align*}
\begin{align*} \frac{|\mathfrak{L}_0(r,\varepsilon )|}{\left |{\left \{{z\in \mathbb{Z}^{q-1}\;:\;\|z-r\|_\infty \leq \varepsilon \sqrt{\Delta }}\right \}}\right |}\sim q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}. \end{align*}
Therefore, w.h.p. for all
![]() $r\in \mathfrak{L}_0$
we have
$r\in \mathfrak{L}_0$
we have
Finally, we observe that
Indeed, since the
![]() $\boldsymbol{\xi }_{ij}$
are uniform and independent, for each
$\boldsymbol{\xi }_{ij}$
are uniform and independent, for each
![]() $i\in [m]$
we have
$i\in [m]$
we have
![]() $\sum _{j=1}^{k_i}\chi _{i,j}\boldsymbol{\xi }_{ij}=0$
with probability
$\sum _{j=1}^{k_i}\chi _{i,j}\boldsymbol{\xi }_{ij}=0$
with probability
![]() $1/q$
independently. Combining (7.40)–(7.42) completes the proof.
$1/q$
independently. Combining (7.40)–(7.42) completes the proof.
7.5 Proof of Lemma 7.11
We continue to denote by
![]() $\boldsymbol{\sigma }\in \mathbb{F}_q^n$
a uniformly random assignment and by
$\boldsymbol{\sigma }\in \mathbb{F}_q^n$
a uniformly random assignment and by
![]() ${\boldsymbol{I}}_{(q-1)\times (q-1)}$
the
${\boldsymbol{I}}_{(q-1)\times (q-1)}$
the
![]() $(q-1)\times (q-1)$
-identity matrix. Also recall
$(q-1)\times (q-1)$
-identity matrix. Also recall
![]() $\rho _\sigma$
from (7.1) and for
$\rho _\sigma$
from (7.1) and for
![]() $\rho =(\rho (s))_{s\in \mathbb{F}_q}$
obtain
$\rho =(\rho (s))_{s\in \mathbb{F}_q}$
obtain
![]() $\hat{\rho }=(\rho (s))_{s\in \mathbb{F}_q^*}$
by dropping the
$\hat{\rho }=(\rho (s))_{s\in \mathbb{F}_q^*}$
by dropping the
![]() $0$
-entry. The following claim, which we prove via the local limit theorem for sums of independent random variables, determines the distribution of
$0$
-entry. The following claim, which we prove via the local limit theorem for sums of independent random variables, determines the distribution of
![]() $\rho _{\boldsymbol{\sigma }}$
. Let
$\rho _{\boldsymbol{\sigma }}$
. Let
![]() $\bar \rho =q^{-1}\Delta {\mathbb{1}}_{q-1}$
.
$\bar \rho =q^{-1}\Delta {\mathbb{1}}_{q-1}$
.
Claim 7.17.
Let
![]() $\mathcal{C}$
be the
$\mathcal{C}$
be the
![]() $(q-1)\times (q-1)$
-matrix from (7.20) and
$(q-1)\times (q-1)$
-matrix from (7.20) and
![]() $\Delta _2 = \sum _{i=1}^n d_i^2$
. Then w.h.p. for all
$\Delta _2 = \sum _{i=1}^n d_i^2$
. Then w.h.p. for all
![]() $\rho \in \mathfrak{P}_q$
we have
$\rho \in \mathfrak{P}_q$
we have
The proof of Claim 7.17 is based on local limit theorem techniques similar to but simpler than the ones from Section 7.4. In fact, the proof strategy is somewhat reminiscent of that of the well-known local limit theorem for sums of independent random vectors from [Reference Davis and McDonald18]. However, the local theorem from that paper does not imply Claim 7.17 directly because a key assumption (that increments of vectors in each direction can be realised) is not satisfied here. We therefore carry the details out in the appendix.
Claim 7.17 demonstrates that
![]() $\rho _{\boldsymbol{\sigma }}$
satisfies a local limit theorem. Hence, let
$\rho _{\boldsymbol{\sigma }}$
satisfies a local limit theorem. Hence, let
![]() $\textbf{N}'\in{\mathbb{R}}^{q-1}$
be a mean-zero Gaussian vector with covariance matrix
$\textbf{N}'\in{\mathbb{R}}^{q-1}$
be a mean-zero Gaussian vector with covariance matrix
![]() $\mathcal{C}$
. Moreover, fix
$\mathcal{C}$
. Moreover, fix
![]() $\varepsilon \gt 0$
and let
$\varepsilon \gt 0$
and let
![]() $U=v+[-\varepsilon,\varepsilon ]^{q-1}\subseteq{\mathbb{R}}^{q-1}$
be a box of side length
$U=v+[-\varepsilon,\varepsilon ]^{q-1}\subseteq{\mathbb{R}}^{q-1}$
be a box of side length
![]() $2\varepsilon$
. Then w.h.p. we have
$2\varepsilon$
. Then w.h.p. we have
where
![]() $\Delta _2$
is as in Claim 7.17. This can be seen as in the proof of Lemma 7.8. Indeed, Claim 7.17 implies that
$\Delta _2$
is as in Claim 7.17. This can be seen as in the proof of Lemma 7.8. Indeed, Claim 7.17 implies that
![]() $\hat{\rho }_{\boldsymbol{\sigma }}$
is asymptotically uniformly distributed on the lattice points of the box
$\hat{\rho }_{\boldsymbol{\sigma }}$
is asymptotically uniformly distributed on the lattice points of the box
![]() $\Delta _2(U+q^{-1}\Delta {\mathbb{1}})$
whose coordinates are divisible by
$\Delta _2(U+q^{-1}\Delta {\mathbb{1}})$
whose coordinates are divisible by
![]() $\mathfrak{d}$
w.h.p. Thus, w.h.p. for any
$\mathfrak{d}$
w.h.p. Thus, w.h.p. for any
![]() $z,z'\in{\Delta _2(U+q^{-1}\Delta {\mathbb{1}})} \cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
we have
$z,z'\in{\Delta _2(U+q^{-1}\Delta {\mathbb{1}})} \cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
we have
Let
![]() $\tilde U = \Delta _2(U+q^{-1}\Delta {\mathbb{1}})$
. Moreover, we claim that
$\tilde U = \Delta _2(U+q^{-1}\Delta {\mathbb{1}})$
. Moreover, we claim that
 \begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0\mid \hat{\rho }_{\boldsymbol{\sigma }}\in{\tilde U}}\right \rbrack \sim \frac{\left |{{\tilde{U}}\cap \mathfrak{L}_0\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}{\left |{{\tilde{U}}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}\leq \frac{\left |{{\tilde U}\cap \mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}{\left |{{\tilde U} \cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}&\leq (1+o(1))q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}. \end{align}
\begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0\mid \hat{\rho }_{\boldsymbol{\sigma }}\in{\tilde U}}\right \rbrack \sim \frac{\left |{{\tilde{U}}\cap \mathfrak{L}_0\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}{\left |{{\tilde{U}}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}\leq \frac{\left |{{\tilde U}\cap \mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}{\left |{{\tilde U} \cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}}\right |}&\leq (1+o(1))q^{-{\mathbb{1}}\{|{\text{supp}}\boldsymbol{\chi }|=1\}}. \end{align}
Indeed, if
![]() $|{\text{supp}}\boldsymbol{\chi }|\gt 1$
, then (7.45) is satisfied w.h.p. for the trivial reason that the r.h.s. equals
$|{\text{supp}}\boldsymbol{\chi }|\gt 1$
, then (7.45) is satisfied w.h.p. for the trivial reason that the r.h.s. equals
![]() $1+o(1)$
. Hence, suppose that
$1+o(1)$
. Hence, suppose that
![]() $|{\text{supp}}\boldsymbol{\chi }|=1$
, let
$|{\text{supp}}\boldsymbol{\chi }|=1$
, let
![]() $\mathfrak{M}\supset \mathfrak{L}_0$
be the module from Proposition 2.5 and let
$\mathfrak{M}\supset \mathfrak{L}_0$
be the module from Proposition 2.5 and let
![]() $\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
be its assorted basis. Clearly,
$\mathfrak{b}_1,\ldots,\mathfrak{b}_{q-1}$
be its assorted basis. Clearly,
![]() $\mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}\supseteq \mathfrak{d}\mathfrak{M}$
. Conversely, Cramer’s rule shows that any
$\mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}\supseteq \mathfrak{d}\mathfrak{M}$
. Conversely, Cramer’s rule shows that any
![]() $y\in \mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
can be expressed as
$y\in \mathfrak{M}\cap \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
can be expressed as
In particular, all coordinates
![]() $z_i$
are divisible by
$z_i$
are divisible by
![]() $\mathfrak{d}$
because
$\mathfrak{d}$
because
![]() $y\in \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
. Hence,
$y\in \mathfrak{d}\mathbb{Z}^{\mathbb{F}_q^*}$
. Hence,
![]() $y\in \mathfrak{d}\mathfrak{M}$
because
$y\in \mathfrak{d}\mathfrak{M}$
because
![]() $\mathfrak{d}$
and
$\mathfrak{d}$
and
![]() $q$
are coprime. Lemma 3.6 therefore implies (7.45). Finally, the assertion follows from (7.43)–(7.45).
$q$
are coprime. Lemma 3.6 therefore implies (7.45). Finally, the assertion follows from (7.43)–(7.45).
8. Proof of Proposition 4.1
We prove Proposition 4.1 by way of a coupling argument inspired by the Aizenman-Sims-Starr scheme from spin glass theory [Reference Aizenman, Sims and Starr5]. The proof is a close adaptation of the coupling argument used in [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10] to prove the approximate rank formula (1.4). We will therefore be able to reuse some of the technical steps from that paper. The main difference is that we need to accommodate the extra ternary equations
![]() $t_i$
. Their presence gives rise to the second parameter
$t_i$
. Their presence gives rise to the second parameter
![]() $\beta$
in (4.5).
$\beta$
in (4.5).
8.1 Overview
The basic idea behind the Aizenman-Sims-Starr scheme is to compute the expected difference
![]() $\mathbb{E}[\text{nul}{\boldsymbol{A}}[n+1,\varepsilon,\delta,\Theta ]]-{\mathbb{E}[\text{nul}{\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]]}$
of the nullity upon increasing the size of the matrix. We then obtain (4.5) by writing a telescoping sum. In order to estimate the expected change of the nullity, we set up a coupling of
$\mathbb{E}[\text{nul}{\boldsymbol{A}}[n+1,\varepsilon,\delta,\Theta ]]-{\mathbb{E}[\text{nul}{\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]]}$
of the nullity upon increasing the size of the matrix. We then obtain (4.5) by writing a telescoping sum. In order to estimate the expected change of the nullity, we set up a coupling of
![]() ${\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]$
and
${\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ]$
and
![]() ${\boldsymbol{A}}[n+1,\varepsilon,\delta,\Theta ]$
.
${\boldsymbol{A}}[n+1,\varepsilon,\delta,\Theta ]$
.
To this end it is helpful to work with a description of the random matrix model that is different from the earlier definition of the model in Section 4, which is closer to the original matrix model. The present modification is owed to the fact that it will turn out beneficial to actually order the check variables according to their degree: Specifically, let
![]() ${\boldsymbol{M}}=({\boldsymbol{M}}_j)_{j\geq 1}$
,
${\boldsymbol{M}}=({\boldsymbol{M}}_j)_{j\geq 1}$
,
![]() ${\boldsymbol{\Delta }}=({\boldsymbol{\Delta }}_j)_{j\geq 1}$
,
${\boldsymbol{\Delta }}=({\boldsymbol{\Delta }}_j)_{j\geq 1}$
,
![]() $\boldsymbol{\lambda }$
and
$\boldsymbol{\lambda }$
and
![]() $\boldsymbol{\eta }$
be Poisson variables with means
$\boldsymbol{\eta }$
be Poisson variables with means
 \begin{align} \mathbb{E}[{\boldsymbol{M}}_j]&=(1-\varepsilon ){\mathbb{P}}\left \lbrack{{\boldsymbol{k}}=j}\right \rbrack dn/k, \qquad \quad \mathbb{E}[{\boldsymbol{\Delta }}_j]=(1-\varepsilon ){\mathbb{P}}\left \lbrack{{\boldsymbol{k}}=j}\right \rbrack d/k, \qquad \quad \mathbb{E}\left \lbrack{\boldsymbol{\lambda }}\right \rbrack =\delta n, \nonumber \\[5pt] \mathbb{E}\left \lbrack{\boldsymbol{\eta }}\right \rbrack &= \delta . \end{align}
\begin{align} \mathbb{E}[{\boldsymbol{M}}_j]&=(1-\varepsilon ){\mathbb{P}}\left \lbrack{{\boldsymbol{k}}=j}\right \rbrack dn/k, \qquad \quad \mathbb{E}[{\boldsymbol{\Delta }}_j]=(1-\varepsilon ){\mathbb{P}}\left \lbrack{{\boldsymbol{k}}=j}\right \rbrack d/k, \qquad \quad \mathbb{E}\left \lbrack{\boldsymbol{\lambda }}\right \rbrack =\delta n, \nonumber \\[5pt] \mathbb{E}\left \lbrack{\boldsymbol{\eta }}\right \rbrack &= \delta . \end{align}
All these random variables are mutually independent and independent of
![]() $\boldsymbol{\theta }$
and the
$\boldsymbol{\theta }$
and the
![]() $({\boldsymbol{d}}_i)_{i\geq 1}$
. Further, let
$({\boldsymbol{d}}_i)_{i\geq 1}$
. Further, let
Since
![]() $\sum _{j\geq 1}{\boldsymbol{M}}_j\,\sim \,\text{Po}((1-\varepsilon )dn/k)$
, (8.2) is consistent with (4.1).
$\sum _{j\geq 1}{\boldsymbol{M}}_j\,\sim \,\text{Po}((1-\varepsilon )dn/k)$
, (8.2) is consistent with (4.1).
We define a random Tanner (multi-)graph
![]() ${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
with variable nodes
${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
with variable nodes
![]() $x_1,\ldots,x_n$
and check nodes
$x_1,\ldots,x_n$
and check nodes
![]() $a_{i,j}$
,
$a_{i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{M}}_i]$
,
$j\in [{\boldsymbol{M}}_i]$
,
![]() $t_1, \ldots, t_{\boldsymbol{\lambda }}$
and
$t_1, \ldots, t_{\boldsymbol{\lambda }}$
and
![]() $p_1,\ldots,p_{\boldsymbol{\theta }}$
. Here, the first index of each check variable
$p_1,\ldots,p_{\boldsymbol{\theta }}$
. Here, the first index of each check variable
![]() $a_{i,j}$
will indicate its degree. The edges between variables and the check nodes
$a_{i,j}$
will indicate its degree. The edges between variables and the check nodes
![]() $a_{i,j}$
are induced by a random maximal matching
$a_{i,j}$
are induced by a random maximal matching
![]() $\boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}}\right \rbrack$
of the complete bipartite graph with vertex classes
$\boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}}\right \rbrack$
of the complete bipartite graph with vertex classes
 \begin{align*} \bigcup _{h=1}^n\{x_h\}\times [{\boldsymbol{d}}_h]\quad \mbox{and}\quad \bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol{M}}_i}\{a_{i,j}\}\times [i]. \end{align*}
\begin{align*} \bigcup _{h=1}^n\{x_h\}\times [{\boldsymbol{d}}_h]\quad \mbox{and}\quad \bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol{M}}_i}\{a_{i,j}\}\times [i]. \end{align*}
Moreover, for each
![]() $j \in [\boldsymbol{\lambda }]$
we choose
$j \in [\boldsymbol{\lambda }]$
we choose
![]() $\textbf{i}_{j,1}, \textbf{i}_{j,2}, \textbf{i}_{j,3}$
uniformly and independently from
$\textbf{i}_{j,1}, \textbf{i}_{j,2}, \textbf{i}_{j,3}$
uniformly and independently from
![]() $[n]$
and add edges between
$[n]$
and add edges between
![]() $x_{\textbf{i}_{j,1}}$
,
$x_{\textbf{i}_{j,1}}$
,
![]() $x_{\textbf{i}_{j,2}}$
,
$x_{\textbf{i}_{j,2}}$
,
![]() $x_{\textbf{i}_{j,3}}$
and
$x_{\textbf{i}_{j,3}}$
and
![]() $t_j$
. In addition, we insert an edge between
$t_j$
. In addition, we insert an edge between
![]() $p_i$
and
$p_i$
and
![]() $x_i$
for every
$x_i$
for every
![]() $i\in [\boldsymbol{\theta }]$
.
$i\in [\boldsymbol{\theta }]$
.
To define the random matrix
![]() ${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
to go with
${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
to go with
![]() ${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
, let
${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
, let
 \begin{align} {\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack _{a_{i,j},x_h}&=\boldsymbol{\chi }_{i, h} \sum _{\ell =1}^i\sum _{s=1}^{{\boldsymbol{d}}_h} {\mathbb{1}} \{(x_h, s), (a_{i,j}, \ell )\}\in \boldsymbol{\Gamma }_{n, {\boldsymbol{M}}}\}&&(i\ge 1, j\in [{\boldsymbol{M}}_i], h\in [n]), \end{align}
\begin{align} {\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack _{a_{i,j},x_h}&=\boldsymbol{\chi }_{i, h} \sum _{\ell =1}^i\sum _{s=1}^{{\boldsymbol{d}}_h} {\mathbb{1}} \{(x_h, s), (a_{i,j}, \ell )\}\in \boldsymbol{\Gamma }_{n, {\boldsymbol{M}}}\}&&(i\ge 1, j\in [{\boldsymbol{M}}_i], h\in [n]), \end{align}
 \begin{align} {\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack _{t_i,x_h}&=\boldsymbol{\chi }_{{\boldsymbol{m}}_{\varepsilon,n}+i, h} \sum _{\ell =1}^3{\mathbb{1}}\{\textbf{i}_{i,\ell } = h\} &&(i\in [\boldsymbol{\lambda }],h\in [n]). \end{align}
\begin{align} {\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack _{t_i,x_h}&=\boldsymbol{\chi }_{{\boldsymbol{m}}_{\varepsilon,n}+i, h} \sum _{\ell =1}^3{\mathbb{1}}\{\textbf{i}_{i,\ell } = h\} &&(i\in [\boldsymbol{\lambda }],h\in [n]). \end{align}
The Tanner graph
![]() ${\boldsymbol{G}}\left \lbrack{n+1, {\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
and its associated random matrix
${\boldsymbol{G}}\left \lbrack{n+1, {\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
and its associated random matrix
![]() ${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
are defined analogously using
${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
are defined analogously using
![]() $n+1$
variable nodes instead of
$n+1$
variable nodes instead of
![]() $n$
,
$n$
,
![]() ${\boldsymbol{M}}^+$
instead of
${\boldsymbol{M}}^+$
instead of
![]() ${\boldsymbol{M}}$
and
${\boldsymbol{M}}$
and
![]() $\boldsymbol{\lambda }^+$
instead of
$\boldsymbol{\lambda }^+$
instead of
![]() $\boldsymbol{\lambda }$
.
$\boldsymbol{\lambda }$
.
Fact 8.1.
For any
![]() $\varepsilon, \delta \gt 0$
we have
$\varepsilon, \delta \gt 0$
we have
Proof. Because the check degrees
![]() ${\boldsymbol{k}}_i$
of the random factor graph
${\boldsymbol{k}}_i$
of the random factor graph
![]() $\textbf{G}\left \lbrack{n,\varepsilon, \delta,\Theta }\right \rbrack$
are drawn independently, the only difference between
$\textbf{G}\left \lbrack{n,\varepsilon, \delta,\Theta }\right \rbrack$
are drawn independently, the only difference between
![]() ${\boldsymbol{G}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
and
${\boldsymbol{G}}\left \lbrack{n,\varepsilon,\delta,\Theta }\right \rbrack$
and
![]() ${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
is the bookkeeping of the number of checks of each degree. The same is true of
${\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
is the bookkeeping of the number of checks of each degree. The same is true of
![]() ${\boldsymbol{G}}\left \lbrack{n+1,\varepsilon,\delta,\Theta }\right \rbrack$
and
${\boldsymbol{G}}\left \lbrack{n+1,\varepsilon,\delta,\Theta }\right \rbrack$
and
![]() ${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
.
${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
.
To construct a coupling of
![]() ${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
and
${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}},\boldsymbol{\lambda }}\right \rbrack$
and
![]() ${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
we introduce a third, intermediate random matrix. Hence, let
${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
we introduce a third, intermediate random matrix. Hence, let
![]() ${\boldsymbol{\gamma }}_i\ge 0$
be the number of checks
${\boldsymbol{\gamma }}_i\ge 0$
be the number of checks
![]() $a_{i,j}$
,
$a_{i,j}$
,
![]() $j\in [{\boldsymbol{M}}_i^+]$
, adjacent to the last variable node
$j\in [{\boldsymbol{M}}_i^+]$
, adjacent to the last variable node
![]() $x_{n+1}$
in
$x_{n+1}$
in
![]() ${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+}\right \rbrack$
. Set
${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+}\right \rbrack$
. Set
![]() ${\boldsymbol{\gamma }}=({\boldsymbol{\gamma }}_i)_{i\geq 3}$
. Also let
${\boldsymbol{\gamma }}=({\boldsymbol{\gamma }}_i)_{i\geq 3}$
. Also let
be the expected number of extra ternary checks of
![]() ${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
in which
${\boldsymbol{G}}\left \lbrack{n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+}\right \rbrack$
in which
![]() $x_{n+1}$
does not appear (recall that each of the
$x_{n+1}$
does not appear (recall that each of the
![]() $\text{Po}(\delta (n+1))$
ternary checks chooses its variables independently and uniformly at random from all
$\text{Po}(\delta (n+1))$
ternary checks chooses its variables independently and uniformly at random from all
![]() $(n+1)^3$
possibilities). Let
$(n+1)^3$
possibilities). Let
Consider the random Tanner graph
![]() ${\boldsymbol{G}}'={\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}}^-,\boldsymbol{\lambda }^-}\right \rbrack$
induced by a random maximal matching
${\boldsymbol{G}}'={\boldsymbol{G}}\left \lbrack{n,{\boldsymbol{M}}^-,\boldsymbol{\lambda }^-}\right \rbrack$
induced by a random maximal matching
![]() $\boldsymbol{\Gamma }'=\boldsymbol{\Gamma }\left \lbrack{n, {\boldsymbol{M}}^-}\right \rbrack$
of the complete bipartite graph with vertex classes
$\boldsymbol{\Gamma }'=\boldsymbol{\Gamma }\left \lbrack{n, {\boldsymbol{M}}^-}\right \rbrack$
of the complete bipartite graph with vertex classes
 \begin{align} \bigcup _{h=1}^n\{x_h\}\times [{\boldsymbol{d}}_h]\quad \mbox{and}\quad \bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol{M}}_i^-}\{a_{i,j}\}\times [i]. \end{align}
\begin{align} \bigcup _{h=1}^n\{x_h\}\times [{\boldsymbol{d}}_h]\quad \mbox{and}\quad \bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol{M}}_i^-}\{a_{i,j}\}\times [i]. \end{align}
Each matching edge
![]() $\{(x_h,s),(a_{i,j},\ell )\}\in \boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}^-}\right \rbrack$
induces an edge between
$\{(x_h,s),(a_{i,j},\ell )\}\in \boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}^-}\right \rbrack$
induces an edge between
![]() $x_h$
and
$x_h$
and
![]() $a_{i,j}$
in the Tanner graph. For each
$a_{i,j}$
in the Tanner graph. For each
![]() $j \in [\boldsymbol{\lambda }^-]$
and
$j \in [\boldsymbol{\lambda }^-]$
and
![]() $\textbf{i}^-_{j,1}, \textbf{i}^-_{j,2}, \textbf{i}^-_{j,3}$
uniform and independent in
$\textbf{i}^-_{j,1}, \textbf{i}^-_{j,2}, \textbf{i}^-_{j,3}$
uniform and independent in
![]() $[n]$
, we add the edges between
$[n]$
, we add the edges between
![]() $x_{\textbf{i}^-_{j,1}}$
,
$x_{\textbf{i}^-_{j,1}}$
,
![]() $x_{\textbf{i}^-_{j,2}}$
,
$x_{\textbf{i}^-_{j,2}}$
,
![]() $x_{\textbf{i}^-_{j,3}}$
and
$x_{\textbf{i}^-_{j,3}}$
and
![]() $t_j$
. In addition, there is an edge between
$t_j$
. In addition, there is an edge between
![]() $p_i$
and
$p_i$
and
![]() $x_i$
for every
$x_i$
for every
![]() $i\in [\boldsymbol{\theta }]$
. Let
$i\in [\boldsymbol{\theta }]$
. Let
![]() ${\boldsymbol{A}}'$
denote the corresponding random matrix.
${\boldsymbol{A}}'$
denote the corresponding random matrix.
For each variable
![]() $x_i$
,
$x_i$
,
![]() $i=1,\ldots,n$
, let
$i=1,\ldots,n$
, let
![]() $\mathcal{C}$
be the set of clones from
$\mathcal{C}$
be the set of clones from
![]() $\bigcup _{i\in [n]}\{x_i\}\times [{\boldsymbol{d}}_i]$
that
$\bigcup _{i\in [n]}\{x_i\}\times [{\boldsymbol{d}}_i]$
that
![]() $\boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}^-}\right \rbrack$
leaves unmatched. We call the elements of
$\boldsymbol{\Gamma }\left \lbrack{n,{\boldsymbol{M}}^-}\right \rbrack$
leaves unmatched. We call the elements of
![]() $\mathcal{C}$
cavities.
$\mathcal{C}$
cavities.
From
![]() ${\boldsymbol{G}}'$
, we finally construct two further Tanner graphs. Obtain the Tanner graph
${\boldsymbol{G}}'$
, we finally construct two further Tanner graphs. Obtain the Tanner graph
![]() ${\boldsymbol{G}}''$
from
${\boldsymbol{G}}''$
from
![]() ${\boldsymbol{G}}'$
by adding new check nodes
${\boldsymbol{G}}'$
by adding new check nodes
![]() $a''_{\!\!\!\!i,j}$
for each
$a''_{\!\!\!\!i,j}$
for each
![]() $i\geq 3$
,
$i\geq 3$
,
![]() $j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]$
and ternary check nodes
$j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]$
and ternary check nodes
![]() $t''_{\!\!\!\!i}$
for
$t''_{\!\!\!\!i}$
for
![]() $i \in [\boldsymbol{\lambda }'']$
, where
$i \in [\boldsymbol{\lambda }'']$
, where
 \begin{align} {\boldsymbol{\lambda }'' \sim \text{Po}(\delta n - \lambda ^-) =\text{Po}\left ({\delta n\left ({ 1 - \left ({\frac{n}{n+1}}\right )^2}\right )}\right ).} \end{align}
\begin{align} {\boldsymbol{\lambda }'' \sim \text{Po}(\delta n - \lambda ^-) =\text{Po}\left ({\delta n\left ({ 1 - \left ({\frac{n}{n+1}}\right )^2}\right )}\right ).} \end{align}
The new checks
![]() $a''_{\!\!\!\!i,j}$
are joined by a random maximal matching
$a''_{\!\!\!\!i,j}$
are joined by a random maximal matching
![]() $\boldsymbol{\Gamma }''$
of the complete bipartite graph on
$\boldsymbol{\Gamma }''$
of the complete bipartite graph on
Moreover, for each
![]() $j \in [\boldsymbol{\lambda }'']$
we choose
$j \in [\boldsymbol{\lambda }'']$
we choose
![]() $\textbf{i}''_{\!\!\!j,1}, \textbf{i}''_{\!\!\!j,2}, \textbf{i}''_{\!\!\!j,3}\in [n]$
uniformly and independently of everything else and add the edges between
$\textbf{i}''_{\!\!\!j,1}, \textbf{i}''_{\!\!\!j,2}, \textbf{i}''_{\!\!\!j,3}\in [n]$
uniformly and independently of everything else and add the edges between
![]() $x''_{\!\!\!\textbf{i}_{j,1}}$
,
$x''_{\!\!\!\textbf{i}_{j,1}}$
,
![]() $x''_{\!\!\!\textbf{i}_{j,2}}$
,
$x''_{\!\!\!\textbf{i}_{j,2}}$
,
![]() $x''_{\!\!\!\textbf{i}_{j,3}}$
and
$x''_{\!\!\!\textbf{i}_{j,3}}$
and
![]() $t''_{\!\!\!j}$
. Let
$t''_{\!\!\!j}$
. Let
![]() ${\boldsymbol{A}}''$
denote the corresponding random matrix, where as before, each new edge is represented by an independent copy of
${\boldsymbol{A}}''$
denote the corresponding random matrix, where as before, each new edge is represented by an independent copy of
![]() $\boldsymbol{\chi }$
.
$\boldsymbol{\chi }$
.
Finally, let
 \begin{align} {\boldsymbol{\lambda }''' \sim \text{Po}(\delta (n+1) - \lambda ^-)=\text{Po}\left ({\delta (n+1)\left ({1-\left ({\frac{n}{n+1}}\right )^3}\right )}\right ).} \end{align}
\begin{align} {\boldsymbol{\lambda }''' \sim \text{Po}(\delta (n+1) - \lambda ^-)=\text{Po}\left ({\delta (n+1)\left ({1-\left ({\frac{n}{n+1}}\right )^3}\right )}\right ).} \end{align}
We analogously obtain
![]() ${\boldsymbol{G}}'''$
by adding one variable node
${\boldsymbol{G}}'''$
by adding one variable node
![]() $x_{n+1}$
as well as check nodes
$x_{n+1}$
as well as check nodes
![]() $a'''_{\!\!\!\!\!i,j}$
,
$a'''_{\!\!\!\!\!i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{\gamma }}_i]$
,
$j\in [{\boldsymbol{\gamma }}_i]$
,
![]() $b'''_{\!\!\!\!\!i,j}$
,
$b'''_{\!\!\!\!\!i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i]$
,
$j\in [{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i]$
,
![]() $t'''_{\!\!\!\!\!i}\;\;, i \in [\boldsymbol{\lambda }''']$
. The new checks
$t'''_{\!\!\!\!\!i}\;\;, i \in [\boldsymbol{\lambda }''']$
. The new checks
![]() $a'''_{\!\!\!\!\!i,j}$
and
$a'''_{\!\!\!\!\!i,j}$
and
![]() $b'''_{\!\!\!\!\!i,j}$
are connected to
$b'''_{\!\!\!\!\!i,j}$
are connected to
![]() ${\boldsymbol{G}}'$
via a random maximal matching
${\boldsymbol{G}}'$
via a random maximal matching
![]() $\boldsymbol{\Gamma }'''$
of the complete bipartite graph on
$\boldsymbol{\Gamma }'''$
of the complete bipartite graph on
 \begin{equation*}\mbox { $\mathcal {C}\qquad $ and }\qquad \bigcup _{i\geq 1}\left ({\bigcup _{j\in [{\boldsymbol {\gamma }}_i]}\{a'''_{\!\!\!\!\!i,j}\}\times [i-1] \cup \bigcup _{j\in [\boldsymbol {M}_i^+-\boldsymbol {M}_i^{-}-{\boldsymbol {\gamma }}_i]}\{b'''_{\!\!\!\!\!i,j}\}\times [i]}\right ).\end{equation*}
\begin{equation*}\mbox { $\mathcal {C}\qquad $ and }\qquad \bigcup _{i\geq 1}\left ({\bigcup _{j\in [{\boldsymbol {\gamma }}_i]}\{a'''_{\!\!\!\!\!i,j}\}\times [i-1] \cup \bigcup _{j\in [\boldsymbol {M}_i^+-\boldsymbol {M}_i^{-}-{\boldsymbol {\gamma }}_i]}\{b'''_{\!\!\!\!\!i,j}\}\times [i]}\right ).\end{equation*}
For each matching edge we insert the corresponding variable-check edge and in addition each of the check nodes
![]() $a'''_{\!\!\!\!\!i,j}$
gets connected to
$a'''_{\!\!\!\!\!i,j}$
gets connected to
![]() $x_{n+1}$
by exactly one edge. Then we connect each
$x_{n+1}$
by exactly one edge. Then we connect each
![]() $t'''_{\!\!\!\!\!i}\;\;$
to
$t'''_{\!\!\!\!\!i}\;\;$
to
![]() $x'''_{\!\!\!\!\!\textbf{i}_{i,1}}, x'''_{\!\!\!\!\!\textbf{i}_{i,2}}$
and
$x'''_{\!\!\!\!\!\textbf{i}_{i,1}}, x'''_{\!\!\!\!\!\textbf{i}_{i,2}}$
and
![]() $x_{n+1}$
, with
$x_{n+1}$
, with
![]() ${\boldsymbol{i}}'''_{\!\!\!\!\!i,1},{\boldsymbol{i}}'''_{\!\!\!\!\!i,2}\in [n+1]$
chosen uniformly and independently. Once again each edge is represented by an independent copy of
${\boldsymbol{i}}'''_{\!\!\!\!\!i,1},{\boldsymbol{i}}'''_{\!\!\!\!\!i,2}\in [n+1]$
chosen uniformly and independently. Once again each edge is represented by an independent copy of
![]() $\boldsymbol{\chi }$
. Let
$\boldsymbol{\chi }$
. Let
![]() ${\boldsymbol{A}}'''$
denote the resulting random matrix.
${\boldsymbol{A}}'''$
denote the resulting random matrix.

Figure 8. Visualisation of the construction of the auxiliary matrices
![]() ${\boldsymbol{A}}''$
and
${\boldsymbol{A}}''$
and
![]() ${\boldsymbol{A}}'''$
from
${\boldsymbol{A}}'''$
from
![]() ${\boldsymbol{A}}'$
. The matrices are identified with their Tanner graph in the graphical representation.
${\boldsymbol{A}}'$
. The matrices are identified with their Tanner graph in the graphical representation.
The following lemma connects
![]() ${\boldsymbol{A}}'',{\boldsymbol{A}}'''$
with the random matrices
${\boldsymbol{A}}'',{\boldsymbol{A}}'''$
with the random matrices
![]() ${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}}, \boldsymbol{\lambda }}\right \rbrack$
,
${\boldsymbol{A}}\left \lbrack{n,{\boldsymbol{M}}, \boldsymbol{\lambda }}\right \rbrack$
,
![]() ${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+}\right \rbrack$
and thus, in light of Fact 8.1, with
${\boldsymbol{A}}\left \lbrack{n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+}\right \rbrack$
and thus, in light of Fact 8.1, with
![]() ${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta }\right \rbrack$
and
${\boldsymbol{A}}\left \lbrack{n,\varepsilon,\delta }\right \rbrack$
and
![]() ${\boldsymbol{A}}\left \lbrack{n+1,\varepsilon,\delta }\right \rbrack$
(See Fig. 8).
${\boldsymbol{A}}\left \lbrack{n+1,\varepsilon,\delta }\right \rbrack$
(See Fig. 8).
Lemma 8.2.
We have
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}'')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]+o(1)$
and
$\mathbb{E}[\text{nul}({\boldsymbol{A}}'')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]+o(1)$
and
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}''')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]+o(1).$
$\mathbb{E}[\text{nul}({\boldsymbol{A}}''')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]+o(1).$
We defer the simple proof of Lemma 8.2 to Section 8.5.
The core of the proof of Proposition 4.1 is to estimate the difference of the nullities of
![]() ${\boldsymbol{A}}'''$
and
${\boldsymbol{A}}'''$
and
![]() ${\boldsymbol{A}}'$
and of
${\boldsymbol{A}}'$
and of
![]() ${\boldsymbol{A}}''$
and
${\boldsymbol{A}}''$
and
![]() ${\boldsymbol{A}}'$
. The following two lemmas express these differences in terms of two random variables
${\boldsymbol{A}}'$
. The following two lemmas express these differences in terms of two random variables
![]() $\boldsymbol{\alpha },\boldsymbol{\beta }$
. Specifically, let
$\boldsymbol{\alpha },\boldsymbol{\beta }$
. Specifically, let
![]() $\boldsymbol{\alpha }$
be the fraction of frozen cavities of
$\boldsymbol{\alpha }$
be the fraction of frozen cavities of
![]() ${\boldsymbol{A}}'$
and let
${\boldsymbol{A}}'$
and let
![]() $\boldsymbol{\beta }$
be the fraction of frozen variables of
$\boldsymbol{\beta }$
be the fraction of frozen variables of
![]() ${\boldsymbol{A}}'$
.
${\boldsymbol{A}}'$
.
Lemma 8.3.
For large enough
![]() $\Theta (\varepsilon )\gt 0$
and small enough
$\Theta (\varepsilon )\gt 0$
and small enough
![]() $0\lt \delta \lt \delta _0$
we have
$0\lt \delta \lt \delta _0$
we have
 \begin{align*} \mathbb{E}[\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')] &= \mathbb{E}\left \lbrack{\exp\!\left ({-3\delta \boldsymbol{\beta }^2}\right ) D(1-K'(\boldsymbol{\alpha })/k)}\right \rbrack + \frac{d}{k}\mathbb{E}\left \lbrack{K'(\boldsymbol{\alpha })+K(\boldsymbol{\alpha })}\right \rbrack \\[5pt] &\quad- \frac{d(k+1)}{k} - 3\delta \mathbb{E}\left \lbrack{1-\boldsymbol{\beta }^2}\right \rbrack +o_{\varepsilon }(1). \end{align*}
\begin{align*} \mathbb{E}[\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')] &= \mathbb{E}\left \lbrack{\exp\!\left ({-3\delta \boldsymbol{\beta }^2}\right ) D(1-K'(\boldsymbol{\alpha })/k)}\right \rbrack + \frac{d}{k}\mathbb{E}\left \lbrack{K'(\boldsymbol{\alpha })+K(\boldsymbol{\alpha })}\right \rbrack \\[5pt] &\quad- \frac{d(k+1)}{k} - 3\delta \mathbb{E}\left \lbrack{1-\boldsymbol{\beta }^2}\right \rbrack +o_{\varepsilon }(1). \end{align*}
Lemma 8.4.
For large enough
![]() $\Theta (\varepsilon )\gt 0$
and small enough
$\Theta (\varepsilon )\gt 0$
and small enough
![]() $0\lt \delta \lt \delta _0$
we have
$0\lt \delta \lt \delta _0$
we have
After some preparations in Section 8.2 we will prove Lemmas 8.3 and 8.4 in Sections 8.3 and 8.4.
Proof of Proposition
4.1. For any
![]() $\varepsilon, \delta \gt 0$
, by Fact 8.1 and Lemma 8.2, we have
$\varepsilon, \delta \gt 0$
, by Fact 8.1 and Lemma 8.2, we have
 \begin{align*} \limsup _{n\to \infty }\frac{1}{n}\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ])}\right \rbrack &\leq \limsup _{n\to \infty }\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+,\Theta ])}\right \rbrack - \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}},\boldsymbol{\lambda },\Theta ])}\right \rbrack \\[5pt] &\leq \limsup _{n\to \infty }\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''') -\text{nul}({\boldsymbol{A}}')}\right \rbrack - \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}'') -\text{nul}({\boldsymbol{A}}')}\right \rbrack . \end{align*}
\begin{align*} \limsup _{n\to \infty }\frac{1}{n}\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n,\varepsilon,\delta,\Theta ])}\right \rbrack &\leq \limsup _{n\to \infty }\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+,\boldsymbol{\lambda }^+,\Theta ])}\right \rbrack - \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}},\boldsymbol{\lambda },\Theta ])}\right \rbrack \\[5pt] &\leq \limsup _{n\to \infty }\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''') -\text{nul}({\boldsymbol{A}}')}\right \rbrack - \mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}'') -\text{nul}({\boldsymbol{A}}')}\right \rbrack . \end{align*}
For large enough
![]() $\Theta (\varepsilon )\gt 0$
and small enough
$\Theta (\varepsilon )\gt 0$
and small enough
![]() $0\lt \delta \lt \delta _0$
, we can further upper bound the last expression via Lemma 8.3 and Lemma 8.4. Taking the maximum over all possible realisations of the random variables
$0\lt \delta \lt \delta _0$
, we can further upper bound the last expression via Lemma 8.3 and Lemma 8.4. Taking the maximum over all possible realisations of the random variables
![]() $\boldsymbol{\alpha }, \boldsymbol{\beta }$
finishes the proof of Proposition 4.1.
$\boldsymbol{\alpha }, \boldsymbol{\beta }$
finishes the proof of Proposition 4.1.
8.2 Preparations
To facilitate the proofs of Lemmas 8.3 and 8.4 we establish a few basic statements about the coupling. Some of these are immediate consequences of statements from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10], where a similar coupling was used. Let us begin with the following lower bound on the likely number of cavities.
Lemma 8.5.
W.h.p. we have
![]() $|\mathcal{C}|\geq \varepsilon dn/2$
.
$|\mathcal{C}|\geq \varepsilon dn/2$
.
Proof. Apart from the extra ternary check nodes
![]() $t_1, \ldots t_{\boldsymbol{\lambda }'}$
, the construction of
$t_1, \ldots t_{\boldsymbol{\lambda }'}$
, the construction of
![]() ${\boldsymbol{G}}'$
coincides with that of the Tanner graph from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. Because the presence of
${\boldsymbol{G}}'$
coincides with that of the Tanner graph from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. Because the presence of
![]() $t_1, \ldots t_{\boldsymbol{\lambda }'}$
does not affect the number of cavities, the assertion therefore follows from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 5.5].
$t_1, \ldots t_{\boldsymbol{\lambda }'}$
does not affect the number of cavities, the assertion therefore follows from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 5.5].
As a next step we show that w.h.p. the random matrix
![]() ${\boldsymbol{A}}'$
does not have very many short linear relations. Specifically, if we choose a bounded number of variables and a bounded number of cavities randomly, then it is quite unlikely that the chosen coordinates form a proper relation. Formally, let
${\boldsymbol{A}}'$
does not have very many short linear relations. Specifically, if we choose a bounded number of variables and a bounded number of cavities randomly, then it is quite unlikely that the chosen coordinates form a proper relation. Formally, let
![]() $\mathcal{R}(\ell _1,\ell _2)$
be the set of all sequences
$\mathcal{R}(\ell _1,\ell _2)$
be the set of all sequences
![]() $(i_1,\ldots,i_{\ell _1})\in [n]^{\ell _1}$
,
$(i_1,\ldots,i_{\ell _1})\in [n]^{\ell _1}$
,
![]() $(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2})\in \mathcal{C}$
such that
$(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2})\in \mathcal{C}$
such that
![]() $(i_1,\ldots,i_{\ell _1},u_1,\ldots,u_{\ell _2})$
is a proper relation of
$(i_1,\ldots,i_{\ell _1},u_1,\ldots,u_{\ell _2})$
is a proper relation of
![]() ${\boldsymbol{A}}'$
. Furthermore, let
${\boldsymbol{A}}'$
. Furthermore, let
![]() $\mathfrak{R}(\zeta,\ell )$
be the event that
$\mathfrak{R}(\zeta,\ell )$
be the event that
![]() $|\mathcal{R}(\ell _1,\ell _2)|\leq \zeta n^{\ell _1}{|\mathcal{C}|}^{\ell _2}$
for all
$|\mathcal{R}(\ell _1,\ell _2)|\leq \zeta n^{\ell _1}{|\mathcal{C}|}^{\ell _2}$
for all
![]() $0\leq \ell _1,\ell _2\leq \ell$
.
$0\leq \ell _1,\ell _2\leq \ell$
.
Lemma 8.6.
For any
![]() $\zeta \gt 0$
,
$\zeta \gt 0$
,
![]() $\ell \gt 0$
exist
$\ell \gt 0$
exist
![]() $\Theta _0=\Theta _0(\varepsilon,\zeta,\ell )\gt 0$
and
$\Theta _0=\Theta _0(\varepsilon,\zeta,\ell )\gt 0$
and
![]() $n_0\gt 0$
such that for all
$n_0\gt 0$
such that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
![]() $\Theta \geq \Theta _0$
we have
$\Theta \geq \Theta _0$
we have
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{R}(\zeta,\ell )}\right \rbrack \gt 1-\zeta$
.
${\mathbb{P}}\left \lbrack{\mathfrak{R}(\zeta,\ell )}\right \rbrack \gt 1-\zeta$
.
Proof. Fix any
![]() $\ell _1,\ell _2\leq \ell$
such that
$\ell _1,\ell _2\leq \ell$
such that
![]() $\ell _1+\ell _2\gt 0$
and let
$\ell _1+\ell _2\gt 0$
and let
![]() $\mathfrak{R}(\zeta,\ell _1,\ell _2)$
be the event that
$\mathfrak{R}(\zeta,\ell _1,\ell _2)$
be the event that
![]() $|\mathcal{R}(\ell _1,\ell _2)|\lt \zeta n^{\ell _1}|C|^{\ell _2}$
. Then it suffices to show that
$|\mathcal{R}(\ell _1,\ell _2)|\lt \zeta n^{\ell _1}|C|^{\ell _2}$
. Then it suffices to show that
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{R}(\zeta,\ell _1,\ell _2)}\right \rbrack \gt 1-\zeta$
as we can just replace
${\mathbb{P}}\left \lbrack{\mathfrak{R}(\zeta,\ell _1,\ell _2)}\right \rbrack \gt 1-\zeta$
as we can just replace
![]() $\zeta$
by
$\zeta$
by
![]() $\zeta/(\ell +1)^2$
and apply the union bound. To this end we may assume that
$\zeta/(\ell +1)^2$
and apply the union bound. To this end we may assume that
![]() $\zeta \lt \zeta _0(\varepsilon,\ell )$
for a small enough
$\zeta \lt \zeta _0(\varepsilon,\ell )$
for a small enough
![]() $\zeta _0(\varepsilon,\ell )\gt 0$
.
$\zeta _0(\varepsilon,\ell )\gt 0$
.
We will actually estimate
![]() $|\mathcal{R}(\ell _1,\ell _2)|$
on a certain likely event. Specifically, due to Lemma 8.5 we have
$|\mathcal{R}(\ell _1,\ell _2)|$
on a certain likely event. Specifically, due to Lemma 8.5 we have
![]() $|\mathcal{C}|\geq \varepsilon n/2$
w.h.p. In addition, let
$|\mathcal{C}|\geq \varepsilon n/2$
w.h.p. In addition, let
![]() $\mathcal{A}$
be the event that
$\mathcal{A}$
be the event that
![]() ${\boldsymbol{A}}'$
is
${\boldsymbol{A}}'$
is
![]() $(\zeta ^4/L^\ell,\ell )$
-free. Then Proposition 3.4 shows that
$(\zeta ^4/L^\ell,\ell )$
-free. Then Proposition 3.4 shows that
![]() ${\mathbb{P}}\left \lbrack{\mathcal{A}}\right \rbrack \gt 1-\zeta/3$
, provided that
${\mathbb{P}}\left \lbrack{\mathcal{A}}\right \rbrack \gt 1-\zeta/3$
, provided that
![]() $n\geq n_0$
for a large enough
$n\geq n_0$
for a large enough
![]() $n_0=n_0(\zeta,\ell )$
. To see this, consider the matrix
$n_0=n_0(\zeta,\ell )$
. To see this, consider the matrix
![]() ${\boldsymbol{B}}$
obtained from
${\boldsymbol{B}}$
obtained from
![]() ${\boldsymbol{A}}'$
by deleting the rows representing the unary checks
${\boldsymbol{A}}'$
by deleting the rows representing the unary checks
![]() $p_i$
. Then Proposition 3.4 shows that the matrix
$p_i$
. Then Proposition 3.4 shows that the matrix
![]() ${\boldsymbol{B}}[\boldsymbol{\theta }]$
obtained from
${\boldsymbol{B}}[\boldsymbol{\theta }]$
obtained from
![]() ${\boldsymbol{B}}$
via the pinning operation is
${\boldsymbol{B}}$
via the pinning operation is
![]() $(\zeta ^4,L^\ell )$
-free with probability
$(\zeta ^4,L^\ell )$
-free with probability
![]() $1-\zeta/3$
, provided that
$1-\zeta/3$
, provided that
![]() $\Theta$
is chosen sufficiently large. The only difference between
$\Theta$
is chosen sufficiently large. The only difference between
![]() ${\boldsymbol{B}}[\boldsymbol{\theta }]$
and
${\boldsymbol{B}}[\boldsymbol{\theta }]$
and
![]() ${\boldsymbol{A}}'$
is that in the former random matrix we apply the pinning operation to
${\boldsymbol{A}}'$
is that in the former random matrix we apply the pinning operation to
![]() $\boldsymbol{\theta }$
random coordinates, while in
$\boldsymbol{\theta }$
random coordinates, while in
![]() ${\boldsymbol{A}}'$
the unary checks
${\boldsymbol{A}}'$
the unary checks
![]() $p_i$
pin the first
$p_i$
pin the first
![]() $\boldsymbol{\theta }$
coordinates. However, the distribution of
$\boldsymbol{\theta }$
coordinates. However, the distribution of
![]() ${\boldsymbol{A}}'$
is actually invariant under permutations of the columns. Therefore, the matrices
${\boldsymbol{A}}'$
is actually invariant under permutations of the columns. Therefore, the matrices
![]() ${\boldsymbol{A}}'$
and
${\boldsymbol{A}}'$
and
![]() ${\boldsymbol{B}}[\boldsymbol{\theta }]$
are
${\boldsymbol{B}}[\boldsymbol{\theta }]$
are
![]() $(\zeta ^4,L^\ell )$
-free with precisely the same probability. Hence, Proposition 3.4 implies that
$(\zeta ^4,L^\ell )$
-free with precisely the same probability. Hence, Proposition 3.4 implies that
![]() ${\mathbb{P}}\left \lbrack{\mathcal{A}}\right \rbrack \gt 1-\zeta/3$
.
${\mathbb{P}}\left \lbrack{\mathcal{A}}\right \rbrack \gt 1-\zeta/3$
.
Further, Markov’s inequality shows that for any
![]() $L\gt 0$
,
$L\gt 0$
,
 \begin{align*}{\mathbb{P}}\left \lbrack{\sum _{i=1}^n \textbf{d}_i{\mathbb{1}}\{\textbf{d}_i\gt L\}\geq \frac{\varepsilon \zeta ^2 n}{16\ell }}\right \rbrack \leq \frac{16 \ell \mathbb{E}\left \lbrack{\textbf{d}{\mathbb{1}}\{\textbf{d}\gt L\}}\right \rbrack }{\varepsilon \zeta ^2}. \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{\sum _{i=1}^n \textbf{d}_i{\mathbb{1}}\{\textbf{d}_i\gt L\}\geq \frac{\varepsilon \zeta ^2 n}{16\ell }}\right \rbrack \leq \frac{16 \ell \mathbb{E}\left \lbrack{\textbf{d}{\mathbb{1}}\{\textbf{d}\gt L\}}\right \rbrack }{\varepsilon \zeta ^2}. \end{align*}
Therefore, since
![]() $\mathbb{E}\left \lbrack{\textbf{d}}\right \rbrack = O_\varepsilon (1)$
we can choose
$\mathbb{E}\left \lbrack{\textbf{d}}\right \rbrack = O_\varepsilon (1)$
we can choose
![]() $L=L(\varepsilon, \zeta,\ell )\gt 0$
big enough such that the event
$L=L(\varepsilon, \zeta,\ell )\gt 0$
big enough such that the event
 \begin{equation*}\mathcal {L}=\left \{{\sum _{i=1}^n \textbf {d}_i{\mathbb{1}}\{\textbf {d}_i\gt L\}\lt \frac {\varepsilon \zeta ^2 n}{16\ell }}\right \}\end{equation*}
\begin{equation*}\mathcal {L}=\left \{{\sum _{i=1}^n \textbf {d}_i{\mathbb{1}}\{\textbf {d}_i\gt L\}\lt \frac {\varepsilon \zeta ^2 n}{16\ell }}\right \}\end{equation*}
has probability at least
![]() $1-\zeta/3$
. Thus, the event
$1-\zeta/3$
. Thus, the event
![]() $\mathcal{E}=\mathcal{A}\cap \mathcal{L}\cap \{|\mathcal{C}|\geq \varepsilon n/2\}$
satisfies
$\mathcal{E}=\mathcal{A}\cap \mathcal{L}\cap \{|\mathcal{C}|\geq \varepsilon n/2\}$
satisfies
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}}\right \rbrack \gt 1-\zeta .$
Hence, it suffices to show that
${\mathbb{P}}\left \lbrack{\mathcal{E}}\right \rbrack \gt 1-\zeta .$
Hence, it suffices to show that
To bound
![]() $\mathcal{R}(\ell _1,\ell _2)$
on
$\mathcal{R}(\ell _1,\ell _2)$
on
![]() $\mathcal{E}$
we need to take into consideration that the cavities are degree weighted. Hence, let
$\mathcal{E}$
we need to take into consideration that the cavities are degree weighted. Hence, let
![]() $\mathcal{R}'(\ell _1,\ell _2)$
be the set of all sequences
$\mathcal{R}'(\ell _1,\ell _2)$
be the set of all sequences
![]() $(i_1,\ldots,i_{\ell _1},(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2}))\in \mathcal{R}(\ell _1,\ell _2)$
such that the degree of some variable node
$(i_1,\ldots,i_{\ell _1},(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2}))\in \mathcal{R}(\ell _1,\ell _2)$
such that the degree of some variable node
![]() $u_i$
exceeds
$u_i$
exceeds
![]() $L$
. Assuming
$L$
. Assuming
![]() $\ell _2\gt 0$
, on
$\ell _2\gt 0$
, on
![]() $\mathcal{E}$
we have
$\mathcal{E}$
we have
provided that
![]() $\zeta \gt 0$
is small enough. Here, we have used that on
$\zeta \gt 0$
is small enough. Here, we have used that on
![]() $\mathcal{E}$
,
$\mathcal{E}$
,
![]() $|\mathcal{C}| \geq \varepsilon n/ 2$
and thus
$|\mathcal{C}| \geq \varepsilon n/ 2$
and thus
![]() $n^{\ell _1}|\mathcal{C}|^{\ell _2-1} \leq n^{\ell _1}|\mathcal{C}|^{\ell _2} \cdot \frac{2}{\varepsilon n}$
.
$n^{\ell _1}|\mathcal{C}|^{\ell _2-1} \leq n^{\ell _1}|\mathcal{C}|^{\ell _2} \cdot \frac{2}{\varepsilon n}$
.
Finally, we bound the size of
![]() $\mathcal{R}''(\ell _1,\ell _2)=\mathcal{R}(\ell _1,\ell _2)\setminus \mathcal{R}'(\ell _1,\ell _2)$
. Since for any
$\mathcal{R}''(\ell _1,\ell _2)=\mathcal{R}(\ell _1,\ell _2)\setminus \mathcal{R}'(\ell _1,\ell _2)$
. Since for any
![]() $(i_1,\ldots,i_{\ell _1},(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2}))\in \mathcal{R}''(\ell _1,\ell _2)$
the sequence
$(i_1,\ldots,i_{\ell _1},(u_1,j_1),\ldots,(u_{\ell _2},j_{\ell _2}))\in \mathcal{R}''(\ell _1,\ell _2)$
the sequence
![]() $(i_1,\ldots,i_{\ell _1},u_1,\ldots,u_{\ell _2})$
is a proper relation and since there are no more than
$(i_1,\ldots,i_{\ell _1},u_1,\ldots,u_{\ell _2})$
is a proper relation and since there are no more than
![]() $L^{\ell _2}$
ways of choosing the indices
$L^{\ell _2}$
ways of choosing the indices
![]() $j_1,\ldots,j_{\ell _2}$
, on the event
$j_1,\ldots,j_{\ell _2}$
, on the event
![]() $\mathcal{E}$
we have
$\mathcal{E}$
we have
 \begin{align} |\mathcal{R}''(\ell _1,\ell _2)|&\leq \frac{\zeta ^4}{L^\ell }\cdot L^{\ell _2}n^\ell &&\mbox{[because ${\boldsymbol{A}}'$ is $\zeta ^4/L^\ell,\ell )$-free]}\nonumber \\[5pt] &\leq \zeta ^4\left ({\frac{2}{\varepsilon }}\right )^{\ell _2}\cdot n^{\ell _1}|\mathcal{C}|^{\ell _2}&&\mbox{[because $|\mathcal{C}|\gt \varepsilon n/2$]}\nonumber \\[5pt] &\lt \frac \zeta 2n^{\ell _1}|\mathcal{C}|^{\ell _2}, \end{align}
\begin{align} |\mathcal{R}''(\ell _1,\ell _2)|&\leq \frac{\zeta ^4}{L^\ell }\cdot L^{\ell _2}n^\ell &&\mbox{[because ${\boldsymbol{A}}'$ is $\zeta ^4/L^\ell,\ell )$-free]}\nonumber \\[5pt] &\leq \zeta ^4\left ({\frac{2}{\varepsilon }}\right )^{\ell _2}\cdot n^{\ell _1}|\mathcal{C}|^{\ell _2}&&\mbox{[because $|\mathcal{C}|\gt \varepsilon n/2$]}\nonumber \\[5pt] &\lt \frac \zeta 2n^{\ell _1}|\mathcal{C}|^{\ell _2}, \end{align}
provided that
![]() $\zeta \lt \zeta _0(\varepsilon,\ell )$
is sufficiently small. Thus, (8.11) follows from (8.12) and (8.13).
$\zeta \lt \zeta _0(\varepsilon,\ell )$
is sufficiently small. Thus, (8.11) follows from (8.12) and (8.13).
Let
![]() $(\hat{{\boldsymbol{k}}}_i)_{i \geq 1}$
be a sequence of copies of
$(\hat{{\boldsymbol{k}}}_i)_{i \geq 1}$
be a sequence of copies of
![]() $\hat{{\boldsymbol{k}}}$
, mutually independent and independent of everything else. Also let
$\hat{{\boldsymbol{k}}}$
, mutually independent and independent of everything else. Also let
 \begin{align*} \hat{\boldsymbol{\gamma }}_j = \sum _{i=1}^{{\boldsymbol{d}}_{n+2}} {\mathbb{1}}\left \{{\hat{{\boldsymbol{k}}}_i = j}\right \},&& \hat{\boldsymbol{\gamma }} = (\hat{\boldsymbol{\gamma }}_j)_{j \geq 1}. \end{align*}
\begin{align*} \hat{\boldsymbol{\gamma }}_j = \sum _{i=1}^{{\boldsymbol{d}}_{n+2}} {\mathbb{1}}\left \{{\hat{{\boldsymbol{k}}}_i = j}\right \},&& \hat{\boldsymbol{\gamma }} = (\hat{\boldsymbol{\gamma }}_j)_{j \geq 1}. \end{align*}
Additionally, let
![]() $(\hat{\Delta }_j)_{j \geq 3}$
be a family of independent random variables with distribution
$(\hat{\Delta }_j)_{j \geq 3}$
be a family of independent random variables with distribution
Further, let
![]() $\Sigma '$
be the
$\Sigma '$
be the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() ${\boldsymbol{G}}',{\boldsymbol{A}}',\boldsymbol{\theta },\boldsymbol{\lambda }^-,{\boldsymbol{M}}^-,\boldsymbol{\Gamma }_{n,M^-}, (\boldsymbol{\chi }_{i,j,h}')_{i,j,h \geq 1}$
and
${\boldsymbol{G}}',{\boldsymbol{A}}',\boldsymbol{\theta },\boldsymbol{\lambda }^-,{\boldsymbol{M}}^-,\boldsymbol{\Gamma }_{n,M^-}, (\boldsymbol{\chi }_{i,j,h}')_{i,j,h \geq 1}$
and
![]() $({\boldsymbol{d}}_i)_{i \in [n]}$
. In particular,
$({\boldsymbol{d}}_i)_{i \in [n]}$
. In particular,
![]() $\boldsymbol{\alpha }$
and
$\boldsymbol{\alpha }$
and
![]() $\boldsymbol{\beta }$
are
$\boldsymbol{\beta }$
are
![]() $\Sigma '$
-measurable.
$\Sigma '$
-measurable.
Lemma 8.7.
With probability
![]() $1-\text{exp}\left ({-\Omega _\varepsilon (1/\varepsilon )}\right )$
, we have
$1-\text{exp}\left ({-\Omega _\varepsilon (1/\varepsilon )}\right )$
, we have
Proof. Because
![]() ${\boldsymbol{G}}'$
is distributed the same as the Tanner graph from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10], apart from the extra ternary checks
${\boldsymbol{G}}'$
is distributed the same as the Tanner graph from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10], apart from the extra ternary checks
![]() $t_i$
, which do not affect the random vector
$t_i$
, which do not affect the random vector
![]() $\boldsymbol{\gamma }$
, the assertion follows from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 5.8].
$\boldsymbol{\gamma }$
, the assertion follows from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Lemma 5.8].
Let
![]() $\ell _*=\lceil \exp\!(1/\varepsilon ^4)\rceil$
and
$\ell _*=\lceil \exp\!(1/\varepsilon ^4)\rceil$
and
![]() $\delta _*=\exp\!(-1/\varepsilon ^4)$
and consider the event
$\delta _*=\exp\!(-1/\varepsilon ^4)$
and consider the event
Further, consider the event
Corollary 8.8.
For sufficiently large
![]() $\Theta =\Theta (\varepsilon )\gt 0$
we have
$\Theta =\Theta (\varepsilon )\gt 0$
we have
![]() ${\mathbb{P}}\left \lbrack{{\boldsymbol{A}}'\in \mathcal{E}}\right \rbrack \gt \exp\!(-1/\varepsilon ^4)$
. Moreover,
${\mathbb{P}}\left \lbrack{{\boldsymbol{A}}'\in \mathcal{E}}\right \rbrack \gt \exp\!(-1/\varepsilon ^4)$
. Moreover,
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}'}\right \rbrack =1-o(1)$
.
${\mathbb{P}}\left \lbrack{\mathcal{E}'}\right \rbrack =1-o(1)$
.
Proof. The first statement follows from Lemma 8.6. The second statement follows from the choice of the parameters in (8.1), Lemma 3.9 and Lemma 8.5.
With these preparations in place we are ready to proceed to the proofs of Lemmas 8.3 and 8.4.
8.3 Proof of Lemma 8.3
Let
Then the total number of new non-zero entries upon going from
![]() ${\boldsymbol{A}}'$
to
${\boldsymbol{A}}'$
to
![]() ${\boldsymbol{A}}'''$
is bounded by
${\boldsymbol{A}}'''$
is bounded by
![]() ${\boldsymbol{Y}}+{\boldsymbol{Y}}'+3\boldsymbol{\lambda }'''$
. Let
${\boldsymbol{Y}}+{\boldsymbol{Y}}'+3\boldsymbol{\lambda }'''$
. Let
Claim 8.9.
We have
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}''}\right \rbrack =1-O_{\varepsilon }(\varepsilon )$
.
${\mathbb{P}}\left \lbrack{\mathcal{E}''}\right \rbrack =1-O_{\varepsilon }(\varepsilon )$
.
Proof. Apart from the additional ternary checks the argument is similar to [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Proof of Claim 5.9]. The construction (8.1) ensures that
![]() $\mathbb{E}[{\boldsymbol{X}}],\mathbb{E}[{\boldsymbol{Y}}]=O_{\varepsilon }(1)$
. Therefore,
$\mathbb{E}[{\boldsymbol{X}}],\mathbb{E}[{\boldsymbol{Y}}]=O_{\varepsilon }(1)$
. Therefore,
![]() ${\mathbb{P}}\left \lbrack{{\boldsymbol{X}}\gt 1/\varepsilon }\right \rbrack =O_{\varepsilon }(\varepsilon )$
,
${\mathbb{P}}\left \lbrack{{\boldsymbol{X}}\gt 1/\varepsilon }\right \rbrack =O_{\varepsilon }(\varepsilon )$
,
![]() ${\mathbb{P}}\left \lbrack{{\boldsymbol{Y}}\gt 1/\varepsilon }\right \rbrack =O_{\varepsilon }(\varepsilon )$
by Markov’s inequality. Further, a given check node of degree
${\mathbb{P}}\left \lbrack{{\boldsymbol{Y}}\gt 1/\varepsilon }\right \rbrack =O_{\varepsilon }(\varepsilon )$
by Markov’s inequality. Further, a given check node of degree
![]() $i$
is adjacent to
$i$
is adjacent to
![]() $x_{n+1}$
with probability at most
$x_{n+1}$
with probability at most
![]() $i{\boldsymbol{d}}_{n+1}/\sum _{i=1}^n{\boldsymbol{d}}_i\geq n\leq i{\boldsymbol{d}}_{n+1}/n$
. Consequently,
$i{\boldsymbol{d}}_{n+1}/\sum _{i=1}^n{\boldsymbol{d}}_i\geq n\leq i{\boldsymbol{d}}_{n+1}/n$
. Consequently,
Moreover, (8.10) shows that
![]() $\mathbb{E}[\boldsymbol{\lambda }''']=O_\varepsilon (1)$
. Thus, the assertion follows from Markov’s inequality.
$\mathbb{E}[\boldsymbol{\lambda }''']=O_\varepsilon (1)$
. Thus, the assertion follows from Markov’s inequality.
We obtain
![]() ${\boldsymbol{G}}'''$
from
${\boldsymbol{G}}'''$
from
![]() ${\boldsymbol{G}}'$
by adding checks
${\boldsymbol{G}}'$
by adding checks
![]() $a'''_{\!\!\!\!\!i,j}$
,
$a'''_{\!\!\!\!\!i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{\gamma }}_i]$
,
$j\in [{\boldsymbol{\gamma }}_i]$
,
![]() $b'''_{\!\!\!\!\!i,j}$
,
$b'''_{\!\!\!\!\!i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i]$
and
$j\in [{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i]$
and
![]() $t'''_{\!\!\!\!\!i}\;\;$
,
$t'''_{\!\!\!\!\!i}\;\;$
,
![]() $i\in [\boldsymbol{\lambda }''']$
. Let
$i\in [\boldsymbol{\lambda }''']$
. Let
 \begin{equation*}\mathcal {X}'''=\left ({\bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol {\gamma }}_i}\partial a'''_{\!\!\!\!\!i,j}\setminus \{x_{n+1}\}}\right )\cup \left ({\bigcup _{i\geq 1}\bigcup _{j\in [\boldsymbol {M}_i^+-\boldsymbol {M}_i^{-}-{\boldsymbol {\gamma }}_i]}\partial b'''_{\!\!\!\!\!i,j}}\right )\cup \bigcup _{i=1}^{\boldsymbol {\lambda }'''}\partial t'''_{\!\!\!\!\!i}\;\;\setminus \{x_{n+1}\}\end{equation*}
\begin{equation*}\mathcal {X}'''=\left ({\bigcup _{i\geq 1}\bigcup _{j=1}^{{\boldsymbol {\gamma }}_i}\partial a'''_{\!\!\!\!\!i,j}\setminus \{x_{n+1}\}}\right )\cup \left ({\bigcup _{i\geq 1}\bigcup _{j\in [\boldsymbol {M}_i^+-\boldsymbol {M}_i^{-}-{\boldsymbol {\gamma }}_i]}\partial b'''_{\!\!\!\!\!i,j}}\right )\cup \bigcup _{i=1}^{\boldsymbol {\lambda }'''}\partial t'''_{\!\!\!\!\!i}\;\;\setminus \{x_{n+1}\}\end{equation*}
be the set of variable neighbours of these new checks among
![]() $x_1,\ldots,x_n$
. Further, let
$x_1,\ldots,x_n$
. Further, let
 \begin{equation*}\mathcal {E}'''=\left \{{{|\mathcal {X}'''|=\boldsymbol {Y}}+\sum _{i\geq 1}(i-1){\boldsymbol {\gamma }}_i+\boldsymbol {\lambda }'''}\right \}\end{equation*}
\begin{equation*}\mathcal {E}'''=\left \{{{|\mathcal {X}'''|=\boldsymbol {Y}}+\sum _{i\geq 1}(i-1){\boldsymbol {\gamma }}_i+\boldsymbol {\lambda }'''}\right \}\end{equation*}
be the event that the variables of
![]() ${\boldsymbol{G}}'$
where the new checks connect are pairwise distinct.
${\boldsymbol{G}}'$
where the new checks connect are pairwise distinct.
Claim 8.10.
We have
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}'''\mid \mathcal{E}'\cap \mathcal{E}''}\right \rbrack =1-o(1).$
${\mathbb{P}}\left \lbrack{\mathcal{E}'''\mid \mathcal{E}'\cap \mathcal{E}''}\right \rbrack =1-o(1).$
Proof. By the same token as in [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, proof of Claim 5.10], given that
![]() $\mathcal{E}'$
occurs the total number of cavities comes to
$\mathcal{E}'$
occurs the total number of cavities comes to
![]() $\Omega (n)$
. At the same time, the maximum variable node degree is of order
$\Omega (n)$
. At the same time, the maximum variable node degree is of order
![]() $O(\sqrt n)$
. Moreover, given the event
$O(\sqrt n)$
. Moreover, given the event
![]() $\mathcal{E}''$
no more than
$\mathcal{E}''$
no more than
![]() ${\boldsymbol{Y}}+{\boldsymbol{Y}}'=O_{\varepsilon }(1/\varepsilon )$
random cavities are chosen as neighbours of the new checks
${\boldsymbol{Y}}+{\boldsymbol{Y}}'=O_{\varepsilon }(1/\varepsilon )$
random cavities are chosen as neighbours of the new checks
![]() $a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
. Thus, by the birthday paradox the probability that the checks
$a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
. Thus, by the birthday paradox the probability that the checks
![]() $a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
occupy more than one cavity of any variable node is
$a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
occupy more than one cavity of any variable node is
![]() $o(1)$
. Furthermore, the additional ternary nodes
$o(1)$
. Furthermore, the additional ternary nodes
![]() $t'''_{\!\!\!\!\!i}\;\;$
choose their two neighbours among
$t'''_{\!\!\!\!\!i}\;\;$
choose their two neighbours among
![]() $x_1,\ldots,x_n$
mutually independently and independently of the
$x_1,\ldots,x_n$
mutually independently and independently of the
![]() $a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
. Since
$a'''_{\!\!\!\!\!i,j},b'''_{\!\!\!\!\!i,j}$
. Since
![]() $\boldsymbol{\lambda }'''$
is bounded given
$\boldsymbol{\lambda }'''$
is bounded given
![]() $1/\varepsilon$
, the overall probability of choosing the same variable twice is
$1/\varepsilon$
, the overall probability of choosing the same variable twice is
![]() $o(1)$
.
$o(1)$
.
The following claim shows that the unlikely event that
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
does not occur does not contributed significantly to the expected change in nullity.
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
does not occur does not contributed significantly to the expected change in nullity.
Claim 8.11.
We have
![]() $\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right |(1-{\mathbb{1}}\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}''')}\right \rbrack =o_{\varepsilon }(1)$
.
$\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right |(1-{\mathbb{1}}\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}''')}\right \rbrack =o_{\varepsilon }(1)$
.
Proof. We modify the proof of [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.11] to accommodate the extra ternary nodes. Since
![]() ${\boldsymbol{A}}'''$
results from
${\boldsymbol{A}}'''$
results from
![]() ${\boldsymbol{A}}'$
by adding one column and no more than
${\boldsymbol{A}}'$
by adding one column and no more than
![]() ${\boldsymbol{X}}+{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'''$
rows, we have
${\boldsymbol{X}}+{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'''$
rows, we have
![]() $\left |{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right |\leq X+{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'''+1$
. Because
$\left |{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right |\leq X+{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'''+1$
. Because
![]() ${\boldsymbol{X}},{\boldsymbol{d}}_{n+1}^2,{\boldsymbol{\lambda }'''}$
have bounded second moments, the Cauchy-Schwarz inequality therefore yields the estimate
${\boldsymbol{X}},{\boldsymbol{d}}_{n+1}^2,{\boldsymbol{\lambda }'''}$
have bounded second moments, the Cauchy-Schwarz inequality therefore yields the estimate
Moreover, combining Corollary 8.8 and Claims 8.9–8.10, we obtain
Recall that
![]() $\boldsymbol{\alpha }$
denotes the fraction of frozen cavities and
$\boldsymbol{\alpha }$
denotes the fraction of frozen cavities and
![]() $\boldsymbol{\beta }$
the fraction of frozen variables of
$\boldsymbol{\beta }$
the fraction of frozen variables of
![]() ${\boldsymbol{A}}'$
. Further, let
${\boldsymbol{A}}'$
. Further, let
![]() $\Sigma ''\supset \Sigma '$
be the
$\Sigma ''\supset \Sigma '$
be the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\boldsymbol{\theta }$
,
$\boldsymbol{\theta }$
,
![]() ${\boldsymbol{G}}'$
,
${\boldsymbol{G}}'$
,
![]() ${\boldsymbol{A}}'$
,
${\boldsymbol{A}}'$
,
![]() ${\boldsymbol{M}}_-$
,
${\boldsymbol{M}}_-$
,
![]() $({\boldsymbol{d}}_i)_{i\in [n+1]}$
,
$({\boldsymbol{d}}_i)_{i\in [n+1]}$
,
![]() $\boldsymbol{\gamma }$
,
$\boldsymbol{\gamma }$
,
![]() ${\boldsymbol{M}}$
,
${\boldsymbol{M}}$
,
![]() $\boldsymbol{\Delta }$
,
$\boldsymbol{\Delta }$
,
![]() $\boldsymbol{\lambda }^-,\boldsymbol{\lambda }'''$
. Then
$\boldsymbol{\lambda }^-,\boldsymbol{\lambda }'''$
. Then
![]() $\boldsymbol{\alpha },\boldsymbol{\beta }$
as well as
$\boldsymbol{\alpha },\boldsymbol{\beta }$
as well as
![]() $\mathcal{E},\mathcal{E}',\mathcal{E}''$
are
$\mathcal{E},\mathcal{E}',\mathcal{E}''$
are
![]() $\Sigma ''$
-measurable but
$\Sigma ''$
-measurable but
![]() $\mathcal{E}'''$
is not.
$\mathcal{E}'''$
is not.
Claim 8.12.
On the event
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
we have
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
we have
 \begin{align*} \mathbb{E}\!\left \lbrack{\left (\!{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right ){\mathbb{1}}\mathcal{E}'''\mid \Sigma ''}\right \rbrack =o_{\varepsilon }(1)&+(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i}-\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i\\[5pt] & -\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2) -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i). \end{align*}
\begin{align*} \mathbb{E}\!\left \lbrack{\left (\!{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')}\right ){\mathbb{1}}\mathcal{E}'''\mid \Sigma ''}\right \rbrack =o_{\varepsilon }(1)&+(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i}-\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i\\[5pt] & -\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2) -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i). \end{align*}
Proof. We modify the proof of [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.12] by taking the additional ternary checks into consideration. Let
We set up a random matrix
![]() ${\boldsymbol{B}}$
with rows indexed by
${\boldsymbol{B}}$
with rows indexed by
![]() $\mathcal{A}\cup \mathcal{B}\cup \mathcal{T}$
and columns indexed by
$\mathcal{A}\cup \mathcal{B}\cup \mathcal{T}$
and columns indexed by
![]() $V_n=\{x_1,\ldots,x_n\}$
. For a check
$V_n=\{x_1,\ldots,x_n\}$
. For a check
![]() $a\in \mathcal{A}\cup \mathcal{B}\cup \mathcal{T}$
and a variable
$a\in \mathcal{A}\cup \mathcal{B}\cup \mathcal{T}$
and a variable
![]() $x\in V_n$
the
$x\in V_n$
the
![]() $(a,x)$
-entry of
$(a,x)$
-entry of
![]() ${\boldsymbol{B}}$
equals zero unless
${\boldsymbol{B}}$
equals zero unless
![]() $x\in \partial _{{\boldsymbol{G}}'''} a$
. Further, the non-zero entries of
$x\in \partial _{{\boldsymbol{G}}'''} a$
. Further, the non-zero entries of
![]() ${\boldsymbol{B}}$
are independent copies of
${\boldsymbol{B}}$
are independent copies of
![]() $\boldsymbol{\chi }$
. Additionally, obtain
$\boldsymbol{\chi }$
. Additionally, obtain
![]() ${\boldsymbol{B}}_*$
from
${\boldsymbol{B}}_*$
from
![]() ${\boldsymbol{B}}$
by zeroing out the
${\boldsymbol{B}}$
by zeroing out the
![]() $x$
-column for every variable
$x$
-column for every variable
![]() $x\in \mathfrak{F}({\boldsymbol{A}}')$
. Finally, let
$x\in \mathfrak{F}({\boldsymbol{A}}')$
. Finally, let
![]() ${\boldsymbol{C}}\in \mathbb{F}^{\mathcal{A}\cup \mathcal{B}\cup \mathcal{T}}$
be a random vector whose entries
${\boldsymbol{C}}\in \mathbb{F}^{\mathcal{A}\cup \mathcal{B}\cup \mathcal{T}}$
be a random vector whose entries
![]() ${\boldsymbol{C}}_a$
,
${\boldsymbol{C}}_a$
,
![]() $a\in \mathcal{A}\cup \mathcal{T}$
, are independent copies of
$a\in \mathcal{A}\cup \mathcal{T}$
, are independent copies of
![]() $\boldsymbol{\chi }$
, while
$\boldsymbol{\chi }$
, while
![]() ${\boldsymbol{C}}_b=0$
for all
${\boldsymbol{C}}_b=0$
for all
![]() $b\in \mathcal{B}$
.
$b\in \mathcal{B}$
.
If
![]() $\mathcal{E}'''$
occurs,
$\mathcal{E}'''$
occurs,
![]() ${\boldsymbol{B}}$
has row full rank because there is at most one non-zero entry in every column and at least one non-zero entry in every row. Hence,
${\boldsymbol{B}}$
has row full rank because there is at most one non-zero entry in every column and at least one non-zero entry in every row. Hence,
Furthermore, since the rank is invariant under row and column permutations, given
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
we have
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
we have
 \begin{align*} \text{nul}{\boldsymbol{A}}'''&=\text{nul}\begin{pmatrix}{\boldsymbol{A}}'&0\\[5pt] {\boldsymbol{B}}&{\boldsymbol{C}}\end{pmatrix}. \end{align*}
\begin{align*} \text{nul}{\boldsymbol{A}}'''&=\text{nul}\begin{pmatrix}{\boldsymbol{A}}'&0\\[5pt] {\boldsymbol{B}}&{\boldsymbol{C}}\end{pmatrix}. \end{align*}
Moreover, given
![]() $\mathcal{E}'$
the set
$\mathcal{E}'$
the set
![]() $\mathcal{X}'''$
of all non-zero columns of
$\mathcal{X}'''$
of all non-zero columns of
![]() ${\boldsymbol{B}}$
satisfies
${\boldsymbol{B}}$
satisfies
![]() $|\mathcal{X}'''|\leq {\boldsymbol{Y}}+{\boldsymbol{Y}}'+\boldsymbol{\lambda }'''\leq 3/\varepsilon$
while
$|\mathcal{X}'''|\leq {\boldsymbol{Y}}+{\boldsymbol{Y}}'+\boldsymbol{\lambda }'''\leq 3/\varepsilon$
while
![]() $|\mathcal{C}|\geq \varepsilon dn/2$
. Therefore, the set of cavities that
$|\mathcal{C}|\geq \varepsilon dn/2$
. Therefore, the set of cavities that
![]() $\boldsymbol{\Gamma }'''$
occupies is within total variation distance
$\boldsymbol{\Gamma }'''$
occupies is within total variation distance
![]() $o(1)$
of a commensurate number of cavities drawn independently, that is, with replacement. Furthermore, the variables where the checks from
$o(1)$
of a commensurate number of cavities drawn independently, that is, with replacement. Furthermore, the variables where the checks from
![]() $\mathcal{T}$
attach are chosen uniformly at random from
$\mathcal{T}$
attach are chosen uniformly at random from
![]() $x_1,\ldots,x_n$
. Listing the neighbours of
$x_1,\ldots,x_n$
. Listing the neighbours of
![]() $\mathcal{T}$
first and then the cavities chosen as neighbours of checks in
$\mathcal{T}$
first and then the cavities chosen as neighbours of checks in
![]() $\mathcal{A} \cup \mathcal{B}$
, the conditional probability that
$\mathcal{A} \cup \mathcal{B}$
, the conditional probability that
![]() $\mathcal{X}'''$
forms a proper relation of
$\mathcal{X}'''$
forms a proper relation of
![]() ${\boldsymbol{A}}'$
can be upper bounded by the number of such choices that yield proper relations, divided by the total number of choices of variables and cavities. Given
${\boldsymbol{A}}'$
can be upper bounded by the number of such choices that yield proper relations, divided by the total number of choices of variables and cavities. Given
![]() $\mathcal{E}'$
, we had observed that
$\mathcal{E}'$
, we had observed that
![]() $|\mathcal{X}'''|\leq 3/\varepsilon$
. Moreover, on (8.15), for all
$|\mathcal{X}'''|\leq 3/\varepsilon$
. Moreover, on (8.15), for all
![]() $0 \leq \ell _1,\ell _2\leq \ell _\ast = \lceil \exp\!(1/\varepsilon ^4)\rceil$
, the proportion of proper relations among all choices of
$0 \leq \ell _1,\ell _2\leq \ell _\ast = \lceil \exp\!(1/\varepsilon ^4)\rceil$
, the proportion of proper relations among all choices of
![]() $\ell _1$
variables and
$\ell _1$
variables and
![]() $\ell _2$
cavities is at most
$\ell _2$
cavities is at most
![]() $\delta _\ast = \exp\!(-1/\varepsilon ^4)$
. Therefore, on
$\delta _\ast = \exp\!(-1/\varepsilon ^4)$
. Therefore, on
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
the conditional probability given
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
the conditional probability given
![]() $\mathcal{E}'''$
that
$\mathcal{E}'''$
that
![]() $\mathcal{X}'''$
forms a proper relation is bounded by
$\mathcal{X}'''$
forms a proper relation is bounded by
![]() $O_{\varepsilon }(\exp\!(-1/\varepsilon ^4))$
. Consequently, Lemma 3.2 implies that on the event
$O_{\varepsilon }(\exp\!(-1/\varepsilon ^4))$
. Consequently, Lemma 3.2 implies that on the event
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
,
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
,
We are thus left to calculate the rank of
![]() ${\boldsymbol{Q}}=\left ({{\boldsymbol{B}}_*\ {\boldsymbol{C}}}\right )$
. Given
${\boldsymbol{Q}}=\left ({{\boldsymbol{B}}_*\ {\boldsymbol{C}}}\right )$
. Given
![]() $\mathcal{E}'''$
this block matrix decomposes into the
$\mathcal{E}'''$
this block matrix decomposes into the
![]() $\mathcal{A}\cup \mathcal{T}$
-rows
$\mathcal{A}\cup \mathcal{T}$
-rows
![]() ${\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}}$
and the
${\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}}$
and the
![]() $\mathcal{B}$
-rows
$\mathcal{B}$
-rows
![]() ${\boldsymbol{Q}}_{\mathcal{B}}$
such that
${\boldsymbol{Q}}_{\mathcal{B}}$
such that
![]() ${\text{rk}}({\boldsymbol{Q}})={\text{rk}}({\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}})+{\text{rk}}({\boldsymbol{Q}}_{\mathcal{B}})$
. Therefore, it suffices to prove that
${\text{rk}}({\boldsymbol{Q}})={\text{rk}}({\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}})+{\text{rk}}({\boldsymbol{Q}}_{\mathcal{B}})$
. Therefore, it suffices to prove that
 \begin{align} \mathbb{E}\left \lbrack{{\text{rk}}({\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}})\mid \Sigma ''}\right \rbrack &=\lambda '''(1-\boldsymbol{\beta }^2)+\sum _{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right ){\boldsymbol{\gamma }}_i\nonumber \\[5pt] &\quad +1-(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right )^{{\boldsymbol{\gamma }}_i}+o(1). \end{align}
\begin{align} \mathbb{E}\left \lbrack{{\text{rk}}({\boldsymbol{Q}}_{\mathcal{A}\cup \mathcal{T}})\mid \Sigma ''}\right \rbrack &=\lambda '''(1-\boldsymbol{\beta }^2)+\sum _{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right ){\boldsymbol{\gamma }}_i\nonumber \\[5pt] &\quad +1-(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right )^{{\boldsymbol{\gamma }}_i}+o(1). \end{align}
Towards (8.21) consider a check
![]() $b\in \mathcal{B}$
whose corresponding row sports
$b\in \mathcal{B}$
whose corresponding row sports
![]() $i$
non-zero entries. Recall that the fraction
$i$
non-zero entries. Recall that the fraction
![]() $\boldsymbol{\alpha }$
of frozen cavities of
$\boldsymbol{\alpha }$
of frozen cavities of
![]() ${\boldsymbol{A}}'$
is
${\boldsymbol{A}}'$
is
![]() $\Sigma ''$
-measurable and can thus be regarded as constant. Moreover, we may pretend (up to
$\Sigma ''$
-measurable and can thus be regarded as constant. Moreover, we may pretend (up to
![]() $o(1)$
in total variation) that these
$o(1)$
in total variation) that these
![]() $i$
entries are drawn uniformly and independently from the set of cavities, so that the probability that these
$i$
entries are drawn uniformly and independently from the set of cavities, so that the probability that these
![]() $i$
independent and uniform draws all hit frozen cavities comes to
$i$
independent and uniform draws all hit frozen cavities comes to
![]() $\boldsymbol{\alpha }^i+o(1)$
. We emphasise that this calculation only requires the draws to be independent and uniform, but makes no assumption on the underlying dependencies between cavities. Since there are
$\boldsymbol{\alpha }^i+o(1)$
. We emphasise that this calculation only requires the draws to be independent and uniform, but makes no assumption on the underlying dependencies between cavities. Since there are
![]() ${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i$
such checks
${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i$
such checks
![]() $b\in \mathcal{B}$
, we obtain (8.21).
$b\in \mathcal{B}$
, we obtain (8.21).
Moving on to (8.22), consider
![]() $a\in \mathcal{A}$
whose corresponding row has
$a\in \mathcal{A}$
whose corresponding row has
![]() $i-1$
non-zero entries, and recall that
$i-1$
non-zero entries, and recall that
![]() $V_n=\{x_1,\ldots,x_n\}$
. By the same token as in the previous paragraph, the probability that all entries in the
$V_n=\{x_1,\ldots,x_n\}$
. By the same token as in the previous paragraph, the probability that all entries in the
![]() $a$
-row correspond to frozen cavities comes to
$a$
-row correspond to frozen cavities comes to
![]() $\boldsymbol{\alpha }^{i-1}+o(1)$
. Hence, the expected rank of the
$\boldsymbol{\alpha }^{i-1}+o(1)$
. Hence, the expected rank of the
![]() $\mathcal{A}\times V_n$
-minor works out to be
$\mathcal{A}\times V_n$
-minor works out to be
![]() $\sum _{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right ){\boldsymbol{\gamma }}_i+o(1)$
, which is the second summand in (8.22). Similarly, a
$\sum _{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right ){\boldsymbol{\gamma }}_i+o(1)$
, which is the second summand in (8.22). Similarly, a
![]() $t\in \mathcal{T}$
-row adds to the rank unless both the variables in the corresponding check are frozen. The latter event occurs with probability
$t\in \mathcal{T}$
-row adds to the rank unless both the variables in the corresponding check are frozen. The latter event occurs with probability
![]() $\boldsymbol{\beta }^2$
. Hence the first summand. Finally, the
$\boldsymbol{\beta }^2$
. Hence the first summand. Finally, the
![]() ${\boldsymbol{C}}$
-column adds to the rank if none of the
${\boldsymbol{C}}$
-column adds to the rank if none of the
![]() $\mathcal{A}\cup \mathcal{T}$
-rows become all zero, which occurs with probability
$\mathcal{A}\cup \mathcal{T}$
-rows become all zero, which occurs with probability
![]() $(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right )^{{\boldsymbol{\gamma }}_i}+o(1)$
.
$(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}\left ({1-\boldsymbol{\alpha }^{i-1}}\right )^{{\boldsymbol{\gamma }}_i}+o(1)$
.
Proof of Lemma
8.3. Letting
![]() $\mathfrak{E}=\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
and combining Claims 8.9–8.12, we obtain
$\mathfrak{E}=\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
and combining Claims 8.9–8.12, we obtain
 \begin{align} \nonumber \mathbb{E}&\Big |\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')\mid \Sigma ''}\right \rbrack -\Big ((1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i} -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i \\[5pt] &\qquad -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i)-\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2)\Big ){\mathbb{1}}\mathfrak{E}\Big | =o_{\varepsilon }(1). \end{align}
\begin{align} \nonumber \mathbb{E}&\Big |\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')\mid \Sigma ''}\right \rbrack -\Big ((1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i} -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i \\[5pt] &\qquad -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i)-\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2)\Big ){\mathbb{1}}\mathfrak{E}\Big | =o_{\varepsilon }(1). \end{align}
On
![]() $\mathfrak{E}$
all
$\mathfrak{E}$
all
![]() $i$
with
$i$
with
![]() ${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i\gt 0$
are bounded. Moreover, w.h.p. we have
${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^{-}-{\boldsymbol{\gamma }}_i\gt 0$
are bounded. Moreover, w.h.p. we have
![]() ${\boldsymbol{M}}_i\sim \mathbb{E}[{\boldsymbol{M}}_i]=\Omega (n)$
for all bounded
${\boldsymbol{M}}_i\sim \mathbb{E}[{\boldsymbol{M}}_i]=\Omega (n)$
for all bounded
![]() $i$
by Chebyshev’s inequality. Hence, (8.7) implies that
$i$
by Chebyshev’s inequality. Hence, (8.7) implies that
![]() ${\boldsymbol{M}}_i^-={\boldsymbol{M}}_i-{\boldsymbol{\gamma }}_i$
w.h.p. Consequently, (8.23) becomes
${\boldsymbol{M}}_i^-={\boldsymbol{M}}_i-{\boldsymbol{\gamma }}_i$
w.h.p. Consequently, (8.23) becomes
 \begin{align} \nonumber \mathbb{E}\Big |\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')\mid \Sigma ''}\right \rbrack &-\Big ((1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i} -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i \\[5pt] &-\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})\Delta _i-\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2)\Big ){\mathbb{1}}\mathfrak{E}\Big | =o_{\varepsilon }(1). \end{align}
\begin{align} \nonumber \mathbb{E}\Big |\mathbb{E}\left \lbrack{\text{nul}({\boldsymbol{A}}''')-\text{nul}({\boldsymbol{A}}')\mid \Sigma ''}\right \rbrack &-\Big ((1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i} -\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i \\[5pt] &-\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})\Delta _i-\boldsymbol{\lambda }'''(1-\boldsymbol{\beta }^2)\Big ){\mathbb{1}}\mathfrak{E}\Big | =o_{\varepsilon }(1). \end{align}
We proceed to estimate the various terms on the r.h.s. of (8.24) separately. Since
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o_{\varepsilon }(1)$
by Corollary 8.8 and Claims 8.9 and 8.10, Lemma 8.7 yield
${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o_{\varepsilon }(1)$
by Corollary 8.8 and Claims 8.9 and 8.10, Lemma 8.7 yield
 \begin{align} &\nonumber \mathbb{E}\left \lbrack{ {\mathbb{1}}\mathfrak{E}\cdot (1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i}\mid \Sigma ''}\right \rbrack \\[5pt] &=\mathbb{E}\left \lbrack{(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{\hat{\boldsymbol{\gamma }_i}}\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)\nonumber \\[5pt] &=\exp\!(-3\delta \boldsymbol{\beta }^2)D(1-K'(\boldsymbol{\alpha })/k)&\mbox{[by (3.2) and (8.10)]}. \end{align}
\begin{align} &\nonumber \mathbb{E}\left \lbrack{ {\mathbb{1}}\mathfrak{E}\cdot (1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{{\boldsymbol{\gamma }}_i}\mid \Sigma ''}\right \rbrack \\[5pt] &=\mathbb{E}\left \lbrack{(1-\boldsymbol{\beta }^2)^{\boldsymbol{\lambda }'''}\prod_{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})^{\hat{\boldsymbol{\gamma }_i}}\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)\nonumber \\[5pt] &=\exp\!(-3\delta \boldsymbol{\beta }^2)D(1-K'(\boldsymbol{\alpha })/k)&\mbox{[by (3.2) and (8.10)]}. \end{align}
Moreover, since
![]() $\sum _{i\geq 1}{\boldsymbol{\gamma }}_i\leq {\boldsymbol{d}}_{n+1}$
and
$\sum _{i\geq 1}{\boldsymbol{\gamma }}_i\leq {\boldsymbol{d}}_{n+1}$
and
![]() ${\boldsymbol{d}}_{n+1}$
has a bounded second moment, Lemma 8.7 implies that
${\boldsymbol{d}}_{n+1}$
has a bounded second moment, Lemma 8.7 implies that
 \begin{align} \mathbb{E}\left \lbrack{{\mathbb{1}}\mathfrak{E}\cdot \sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i\mid \Sigma ''}\right \rbrack &=\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})\hat{\boldsymbol{\gamma }}_i\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)=d-\frac dkK'(\boldsymbol{\alpha })+o_{\varepsilon }(1). \end{align}
\begin{align} \mathbb{E}\left \lbrack{{\mathbb{1}}\mathfrak{E}\cdot \sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1}){\boldsymbol{\gamma }}_i\mid \Sigma ''}\right \rbrack &=\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i-1})\hat{\boldsymbol{\gamma }}_i\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)=d-\frac dkK'(\boldsymbol{\alpha })+o_{\varepsilon }(1). \end{align}
Further, by Claim 8.9, Lemma 8.7 and (8.14),
 \begin{align} \mathbb{E}\left \lbrack{{\mathbb{1}}\mathfrak{E}\cdot \sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\Delta }}_i\mid \Sigma ''}\right \rbrack &=\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\Delta }}_i\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)=o_{\varepsilon }(1)+\frac dk-\frac dk\mathbb{E}[K(\boldsymbol{\alpha })]. \end{align}
\begin{align} \mathbb{E}\left \lbrack{{\mathbb{1}}\mathfrak{E}\cdot \sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\Delta }}_i\mid \Sigma ''}\right \rbrack &=\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\Delta }}_i\mid \Sigma ''}\right \rbrack +o_{\varepsilon }(1)=o_{\varepsilon }(1)+\frac dk-\frac dk\mathbb{E}[K(\boldsymbol{\alpha })]. \end{align}
Finally, (8.10) yields
8.4 Proof of Lemma 8.4
We proceed similarly as in the proof of Lemma 8.3; actually matters are a bit simpler because we only add checks, while in the proof of Lemma 8.3 we also had to deal with the extra variable node
![]() $x_{n+1}$
. Let
$x_{n+1}$
. Let
![]() $\mathcal{E},\mathcal{E}'$
be the events from (8.15) and (8.16) and let
$\mathcal{E},\mathcal{E}'$
be the events from (8.15) and (8.16) and let
![]() $\mathcal{E}''=\left \{{{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''\leq 1/\varepsilon }\right \}$
. As a direct consequence of the assumption
$\mathcal{E}''=\left \{{{\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''\leq 1/\varepsilon }\right \}$
. As a direct consequence of the assumption
![]() $\mathbb{E}[{\boldsymbol{d}}_{n+1}^2]=O_{\varepsilon,n}(1)$
and of (8.9), we obtain the following.
$\mathbb{E}[{\boldsymbol{d}}_{n+1}^2]=O_{\varepsilon,n}(1)$
and of (8.9), we obtain the following.
Fact 8.13.
We have
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}''}\right \rbrack =1-O_{\varepsilon }(\varepsilon ^2).$
${\mathbb{P}}\left \lbrack{\mathcal{E}''}\right \rbrack =1-O_{\varepsilon }(\varepsilon ^2).$
Let
 \begin{equation*}\mathcal {X}''=\bigcup _{i\geq 1}\bigcup _{j\in [\boldsymbol {M}_i-\boldsymbol {M}_i^-]}\partial _{\boldsymbol {G}''}a''_{\!\!\!\!i,j}\cup \bigcup _{i=1}^{\boldsymbol {\lambda }''}\partial t''_{\!\!\!i}\end{equation*}
\begin{equation*}\mathcal {X}''=\bigcup _{i\geq 1}\bigcup _{j\in [\boldsymbol {M}_i-\boldsymbol {M}_i^-]}\partial _{\boldsymbol {G}''}a''_{\!\!\!\!i,j}\cup \bigcup _{i=1}^{\boldsymbol {\lambda }''}\partial t''_{\!\!\!i}\end{equation*}
be the set of variable nodes where the new checks that we add upon going from
![]() ${\boldsymbol{A}}'$
to
${\boldsymbol{A}}'$
to
![]() ${\boldsymbol{A}}''$
attach. Let
${\boldsymbol{A}}''$
attach. Let
![]() $\mathcal{E}'''$
be the event that in
$\mathcal{E}'''$
be the event that in
![]() ${\boldsymbol{G}}''$
no variable from
${\boldsymbol{G}}''$
no variable from
![]() $\mathcal{X}''$
is connected with the checks
$\mathcal{X}''$
is connected with the checks
![]() $\{a''_{\!\!\!\!i,j} \;:\; i\geq 1,j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]\}\cup \{t''_{\!\!\!i} \;:\; i\in [\boldsymbol{\lambda }'']\}$
by more than one edge.
$\{a''_{\!\!\!\!i,j} \;:\; i\geq 1,j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]\}\cup \{t''_{\!\!\!i} \;:\; i\in [\boldsymbol{\lambda }'']\}$
by more than one edge.
Claim 8.14.
We have
![]() ${\mathbb{P}}\left \lbrack{\mathcal{E}'''\mid \mathcal{E}'\cap \mathcal{E}''}\right \rbrack =1-o(1).$
${\mathbb{P}}\left \lbrack{\mathcal{E}'''\mid \mathcal{E}'\cap \mathcal{E}''}\right \rbrack =1-o(1).$
Proof. This follows from the ‘birthday paradox’ (see the proof of Claim 8.10).
Claim 8.15.
We have
![]() $\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |(1-{\mathbb{1}}\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}''')}\right \rbrack =o_{\varepsilon }(1)$
.
$\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |(1-{\mathbb{1}}\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}''')}\right \rbrack =o_{\varepsilon }(1)$
.
Proof. We have
![]() $\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |\leq {\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''$
as we add at most
$\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |\leq {\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''$
as we add at most
![]() ${\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''$
rows. Because
${\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''$
rows. Because
![]() $\mathbb{E}[({\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'')^2]=O_{\varepsilon }(1)$
by (8.9), Claim 8.13 and the Cauchy-Schwarz inequality yield
$\mathbb{E}[({\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }'')^2]=O_{\varepsilon }(1)$
by (8.9), Claim 8.13 and the Cauchy-Schwarz inequality yield
Moreover, Corollary 8.8 and Claim 8.14 show that
 \begin{align} &\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}}\right \rbrack, \mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}'}\right \rbrack,\nonumber \\[5pt] &\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}'''}\right \rbrack =o_{\varepsilon }(1). \end{align}
\begin{align} &\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}}\right \rbrack, \mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}'}\right \rbrack,\nonumber \\[5pt] &\mathbb{E}\left \lbrack{\left |{\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')}\right |{\mathbb{1}}\mathcal{E}''\setminus \mathcal{E}'''}\right \rbrack =o_{\varepsilon }(1). \end{align}
The matrix
![]() ${\boldsymbol{A}}''$
results from
${\boldsymbol{A}}''$
results from
![]() ${\boldsymbol{A}}'$
by adding checks
${\boldsymbol{A}}'$
by adding checks
![]() $a''_{\!\!\!\!i,j}$
,
$a''_{\!\!\!\!i,j}$
,
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]$
that are connected to random cavities of
$j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]$
that are connected to random cavities of
![]() ${\boldsymbol{A}}'$
.
${\boldsymbol{A}}'$
.
Moreover, as before let
![]() $\Sigma ''\supset \Sigma '$
be the
$\Sigma ''\supset \Sigma '$
be the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\boldsymbol{\theta }$
,
$\boldsymbol{\theta }$
,
![]() ${\boldsymbol{G}}'$
,
${\boldsymbol{G}}'$
,
![]() ${\boldsymbol{A}}'$
,
${\boldsymbol{A}}'$
,
![]() ${\boldsymbol{M}}_-$
,
${\boldsymbol{M}}_-$
,
![]() $({\boldsymbol{d}}_i)_{i\in [n+1]}$
,
$({\boldsymbol{d}}_i)_{i\in [n+1]}$
,
![]() $\boldsymbol{\gamma }$
,
$\boldsymbol{\gamma }$
,
![]() ${\boldsymbol{M}}$
,
${\boldsymbol{M}}$
,
![]() $\boldsymbol{\Delta }$
,
$\boldsymbol{\Delta }$
,
![]() $\boldsymbol{\lambda }^-,\boldsymbol{\lambda }'''$
. Then
$\boldsymbol{\lambda }^-,\boldsymbol{\lambda }'''$
. Then
![]() $\mathcal{E},\mathcal{E}',\mathcal{E}''$
are
$\mathcal{E},\mathcal{E}',\mathcal{E}''$
are
![]() $\Sigma ''$
-measurable, but
$\Sigma ''$
-measurable, but
![]() $\mathcal{E}'''$
is not.
$\mathcal{E}'''$
is not.
Claim 8.16.
On
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
we have
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''$
we have
Proof. Let
![]() $\mathcal{A}=\{a''_{\!\!\!\!i,j} \;:\; i\geq 1,\ j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]\}$
. Moreover, let
$\mathcal{A}=\{a''_{\!\!\!\!i,j} \;:\; i\geq 1,\ j\in [{\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-]\}$
. Moreover, let
![]() $\mathcal{T}$
be the set of new ternary checks
$\mathcal{T}$
be the set of new ternary checks
![]() $t''_{\!\!\!i}$
,
$t''_{\!\!\!i}$
,
![]() $i\in [\boldsymbol{\lambda }'']$
. Let
$i\in [\boldsymbol{\lambda }'']$
. Let
![]() ${\boldsymbol{B}}$
be the
${\boldsymbol{B}}$
be the
![]() $\mathbb{F}_q$
-matrix whose rows are indexed by
$\mathbb{F}_q$
-matrix whose rows are indexed by
![]() $\mathcal{A}\cup \mathcal{T}$
and whose columns are indexed by
$\mathcal{A}\cup \mathcal{T}$
and whose columns are indexed by
![]() $V_n=\{x_1,\ldots,x_n\}$
. The
$V_n=\{x_1,\ldots,x_n\}$
. The
![]() $(a,x)$
-entry of
$(a,x)$
-entry of
![]() ${\boldsymbol{B}}$
is zero unless
${\boldsymbol{B}}$
is zero unless
![]() $a,x$
are adjacent in
$a,x$
are adjacent in
![]() ${\boldsymbol{G}}''$
, in which case the entry is an independent copy of
${\boldsymbol{G}}''$
, in which case the entry is an independent copy of
![]() $\boldsymbol{\chi }$
. Given
$\boldsymbol{\chi }$
. Given
![]() $\mathcal{E}'''$
the matrix
$\mathcal{E}'''$
the matrix
![]() ${\boldsymbol{B}}$
has full row rank
${\boldsymbol{B}}$
has full row rank
![]() ${\text{rk}}({\boldsymbol{B}})=|\mathcal{A}|=\boldsymbol{\lambda }''+\sum _{i\geq 1}{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i$
, because no column contains two non-zero entries and each row has at least one non-zero entry. Further, obtain
${\text{rk}}({\boldsymbol{B}})=|\mathcal{A}|=\boldsymbol{\lambda }''+\sum _{i\geq 1}{\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i$
, because no column contains two non-zero entries and each row has at least one non-zero entry. Further, obtain
![]() ${\boldsymbol{B}}_*$
from
${\boldsymbol{B}}_*$
from
![]() ${\boldsymbol{B}}$
by zeroing out the
${\boldsymbol{B}}$
by zeroing out the
![]() $x$
-column of every
$x$
-column of every
![]() $x\in \mathfrak{F}({\boldsymbol{A}}')$
.
$x\in \mathfrak{F}({\boldsymbol{A}}')$
.
On
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
we see that
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
we see that
 \begin{align} \text{nul}{\boldsymbol{A}}''&=\text{nul}\begin{pmatrix}{\boldsymbol{A}}'\\[5pt] {\boldsymbol{B}}\end{pmatrix}. \end{align}
\begin{align} \text{nul}{\boldsymbol{A}}''&=\text{nul}\begin{pmatrix}{\boldsymbol{A}}'\\[5pt] {\boldsymbol{B}}\end{pmatrix}. \end{align}
Moreover, let
![]() $\mathcal{I}$
be the set of non-zero columns of
$\mathcal{I}$
be the set of non-zero columns of
![]() ${\boldsymbol{B}}$
. Then on
${\boldsymbol{B}}$
. Then on
![]() $\mathcal{E}'\cap \mathcal{E}''$
we have
$\mathcal{E}'\cap \mathcal{E}''$
we have
![]() $|\mathcal{I}|\leq {\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''\leq 1/\varepsilon$
. Hence, on
$|\mathcal{I}|\leq {\boldsymbol{d}}_{n+1}+\boldsymbol{\lambda }''\leq 1/\varepsilon$
. Hence, on
![]() $\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
the probability that
$\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
the probability that
![]() $\mathcal{I}$
forms a proper relation is bounded by
$\mathcal{I}$
forms a proper relation is bounded by
![]() $\exp\!(-1/\varepsilon ^4)$
. Hence, Lemma 3.2 shows
$\exp\!(-1/\varepsilon ^4)$
. Hence, Lemma 3.2 shows
We are thus left to calculate the rank of
![]() ${\boldsymbol{B}}_*$
. Recalling that
${\boldsymbol{B}}_*$
. Recalling that
![]() $\boldsymbol{\alpha }$
stands for the fraction of frozen cavities, we see that for
$\boldsymbol{\alpha }$
stands for the fraction of frozen cavities, we see that for
![]() $a\in \mathcal{A}$
of degree
$a\in \mathcal{A}$
of degree
![]() $i$
the
$i$
the
![]() $a$
-row is all zero in
$a$
-row is all zero in
![]() ${\boldsymbol{B}}_*$
with probability
${\boldsymbol{B}}_*$
with probability
![]() $\boldsymbol{\alpha }^i+o(1)$
. Similarly, for
$\boldsymbol{\alpha }^i+o(1)$
. Similarly, for
![]() $a\in \mathcal{T}$
the
$a\in \mathcal{T}$
the
![]() $a$
-row of
$a$
-row of
![]() ${\boldsymbol{B}}$
gets zeroed out with probability
${\boldsymbol{B}}$
gets zeroed out with probability
![]() $\boldsymbol{\beta }^3$
. Hence, we conclude that
$\boldsymbol{\beta }^3$
. Hence, we conclude that
Proof of Lemma
8.4. Let
![]() $\mathfrak{E}=\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
. Combining Claims 8.15–8.16, we see that
$\mathfrak{E}=\mathcal{E}\cap \mathcal{E}'\cap \mathcal{E}''\cap \mathcal{E}'''$
. Combining Claims 8.15–8.16, we see that
 \begin{align} \mathbb{E}\left |{\mathbb{E}[\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')\mid{\Sigma ''}]+\left ({\boldsymbol{\lambda }''(1-\boldsymbol{\beta }^3)+\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-)}\right ){\mathbb{1}}\mathfrak{E}}\right | &=o_{\varepsilon }(1). \end{align}
\begin{align} \mathbb{E}\left |{\mathbb{E}[\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')\mid{\Sigma ''}]+\left ({\boldsymbol{\lambda }''(1-\boldsymbol{\beta }^3)+\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})({\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-)}\right ){\mathbb{1}}\mathfrak{E}}\right | &=o_{\varepsilon }(1). \end{align}
On
![]() $\mathfrak{E}$
all degrees
$\mathfrak{E}$
all degrees
![]() $i$
with
$i$
with
![]() ${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^-\gt 0$
are bounded. Moreover,
${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^-\gt 0$
are bounded. Moreover,
![]() ${\boldsymbol{M}}_i^-=\Omega (n)$
w.h.p. for every bounded
${\boldsymbol{M}}_i^-=\Omega (n)$
w.h.p. for every bounded
![]() $i$
by Chebyshev’s inequality. Therefore, (8.7) shows that
$i$
by Chebyshev’s inequality. Therefore, (8.7) shows that
![]() ${\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-={\boldsymbol{\gamma }}_i$
for all
${\boldsymbol{M}}_i-{\boldsymbol{M}}_i^-={\boldsymbol{\gamma }}_i$
for all
![]() $i$
with
$i$
with
![]() ${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^-\gt 0$
w.h.p. Hence, (8.34) turns into
${\boldsymbol{M}}_i^+-{\boldsymbol{M}}_i^-\gt 0$
w.h.p. Hence, (8.34) turns into
 \begin{align} \mathbb{E}\left |{\mathbb{E}[\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')\mid{\Sigma ''}]+\left ({\boldsymbol{\lambda }''(1-\boldsymbol{\beta }^3)+\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\gamma }}_i}\right ){\mathbb{1}}\mathfrak{E}}\right | &=o_{\varepsilon }(1). \end{align}
\begin{align} \mathbb{E}\left |{\mathbb{E}[\text{nul}({\boldsymbol{A}}'')-\text{nul}({\boldsymbol{A}}')\mid{\Sigma ''}]+\left ({\boldsymbol{\lambda }''(1-\boldsymbol{\beta }^3)+\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\gamma }}_i}\right ){\mathbb{1}}\mathfrak{E}}\right | &=o_{\varepsilon }(1). \end{align}
We now estimate the two parts of the last expression separately. Since
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o_{\varepsilon }(1)$
by Corollary 8.8, Fact 8.13 and Claim 8.14, the definition (8.9) of
${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o_{\varepsilon }(1)$
by Corollary 8.8, Fact 8.13 and Claim 8.14, the definition (8.9) of
![]() $\boldsymbol{\lambda }''$
yields
$\boldsymbol{\lambda }''$
yields
Moreover, because
![]() $\sum _{i\geq 1}{\boldsymbol{\gamma }}_i\leq {\boldsymbol{d}}_{n+1}$
,
$\sum _{i\geq 1}{\boldsymbol{\gamma }}_i\leq {\boldsymbol{d}}_{n+1}$
,
![]() $\mathbb{E}[{\boldsymbol{d}}_{n+1}]=O_{\varepsilon }(1)$
,
$\mathbb{E}[{\boldsymbol{d}}_{n+1}]=O_{\varepsilon }(1)$
,
 \begin{align} &\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\gamma }}_i{\mathbb{1}}\mathfrak{E}}\right \rbrack \nonumber \\[5pt] &= \mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})\hat{\boldsymbol{\gamma }}_i{\mathbb{1}}\left \{{\boldsymbol{\lambda }''+\sum _{i\geq 1}\hat{\boldsymbol{\gamma }}_i\leq \varepsilon ^{-1/4}}\right \}}\right \rbrack +o_{\varepsilon }(1) && \mbox{[by Lemma 8.7 and Claim,8.13]}\nonumber \\[5pt] &=d\mathbb{E}[1-\boldsymbol{\alpha }^{\hat{{\boldsymbol{k}}}}]+o_{\varepsilon }(1)=d-d\mathbb{E}[\boldsymbol{\alpha } K'(\boldsymbol{\alpha })]/k+o_{\varepsilon }(1)&&\mbox{[by (3.2)].} \end{align}
\begin{align} &\mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i}){\boldsymbol{\gamma }}_i{\mathbb{1}}\mathfrak{E}}\right \rbrack \nonumber \\[5pt] &= \mathbb{E}\left \lbrack{\sum _{i\geq 1}(1-\boldsymbol{\alpha }^{i})\hat{\boldsymbol{\gamma }}_i{\mathbb{1}}\left \{{\boldsymbol{\lambda }''+\sum _{i\geq 1}\hat{\boldsymbol{\gamma }}_i\leq \varepsilon ^{-1/4}}\right \}}\right \rbrack +o_{\varepsilon }(1) && \mbox{[by Lemma 8.7 and Claim,8.13]}\nonumber \\[5pt] &=d\mathbb{E}[1-\boldsymbol{\alpha }^{\hat{{\boldsymbol{k}}}}]+o_{\varepsilon }(1)=d-d\mathbb{E}[\boldsymbol{\alpha } K'(\boldsymbol{\alpha })]/k+o_{\varepsilon }(1)&&\mbox{[by (3.2)].} \end{align}
8.5 Proof of Lemma 8.2
The proof is relatively straightforward, not least because once again we can reuse some technical statements from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10]. Let us deal with
![]() ${\boldsymbol{A}}''$
and
${\boldsymbol{A}}''$
and
![]() ${\boldsymbol{A}}'''$
separately.
${\boldsymbol{A}}'''$
separately.
Claim 8.17.
We have
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}'')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]+o(1)$
.
$\mathbb{E}[\text{nul}({\boldsymbol{A}}'')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]+o(1)$
.
Proof. The matrix models
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]$
and
$\mathbb{E}[\text{nul}({\boldsymbol{A}}[n,{\boldsymbol{M}}, \boldsymbol{\lambda }])]$
and
![]() ${\boldsymbol{A}}''$
coincide with the corresponding models from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17], except that here we add extra ternary checks. Because these extra checks are added independently, the coupling from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17] directly induces a coupling of the enhanced models by attaching the same number
${\boldsymbol{A}}''$
coincide with the corresponding models from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17], except that here we add extra ternary checks. Because these extra checks are added independently, the coupling from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17] directly induces a coupling of the enhanced models by attaching the same number
![]() $\boldsymbol{\lambda }''$
of ternary equations to the same neighbours.
$\boldsymbol{\lambda }''$
of ternary equations to the same neighbours.
Claim 8.18.
We have
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}''')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]+o(1)$
.
$\mathbb{E}[\text{nul}({\boldsymbol{A}}''')]=\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]+o(1)$
.
Proof. The matrix models
![]() $\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]$
and
$\mathbb{E}[\text{nul}({\boldsymbol{A}}[n+1,{\boldsymbol{M}}^+, \boldsymbol{\lambda }^+])]$
and
![]() ${\boldsymbol{A}}'''$
coincide with the corresponding models from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Section 5.5] plus the extra independent ternary equations. Hence, the coupling from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17] yields a coupling of the enhanced models just as in Claim 8.17.
${\boldsymbol{A}}'''$
coincide with the corresponding models from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Section 5.5] plus the extra independent ternary equations. Hence, the coupling from [Reference Coja-Oghlan, Ergür, Gao, Hetterich and Rolvien10, Claim 5.17] yields a coupling of the enhanced models just as in Claim 8.17.
A. Appendix
In this appendix we give a self-contained proof of Claim 7.17, the local limit theorem for sums of independent vectors. We employ a simplified version of the strategy of the proof of Lemma 7.10. Recall that the degree sequences
![]() $(d_1,\ldots,d_n)$
and
$(d_1,\ldots,d_n)$
and
![]() $(k_1,\ldots,k_m)$
satisfy (P1)-(P7) and the notation
$(k_1,\ldots,k_m)$
satisfy (P1)-(P7) and the notation
![]() $\Delta _2 = \sum _{i=1}^n d_i^2$
. Finally, we set
$\Delta _2 = \sum _{i=1}^n d_i^2$
. Finally, we set
As in the proof of Lemma 7.17, given
![]() $\omega \gt 0$
, we choose
$\omega \gt 0$
, we choose
![]() $\varepsilon _0=\varepsilon _0(\omega,q)$
sufficiently small and let
$\varepsilon _0=\varepsilon _0(\omega,q)$
sufficiently small and let
![]() $0\lt \varepsilon \lt \varepsilon _0$
. With these parameters, we set
$0\lt \varepsilon \lt \varepsilon _0$
. With these parameters, we set
 \begin{align*} \mathfrak{L}_0&=\left \{{r\in \mathbb{Z}^{\mathbb{F}_q^\ast } \;:\; {\mathbb{P}}_{\mathfrak{A}}\left ({\hat{\rho }_{\boldsymbol{\sigma }} =r}\right )\gt 0 \text{ and } \left \| r- q^{-1} \Delta {\mathbb{1}} \right \|_1\lt \omega n^{-1/2} \Delta }\right \} \quad \text{ and }\\[5pt] \mathfrak{L}_0(r_*,\varepsilon )&=\left \{{r\in \mathfrak{L}_0 \;:\; \|r-r_*\|_\infty \lt \varepsilon s_n}\right \}. \end{align*}
\begin{align*} \mathfrak{L}_0&=\left \{{r\in \mathbb{Z}^{\mathbb{F}_q^\ast } \;:\; {\mathbb{P}}_{\mathfrak{A}}\left ({\hat{\rho }_{\boldsymbol{\sigma }} =r}\right )\gt 0 \text{ and } \left \| r- q^{-1} \Delta {\mathbb{1}} \right \|_1\lt \omega n^{-1/2} \Delta }\right \} \quad \text{ and }\\[5pt] \mathfrak{L}_0(r_*,\varepsilon )&=\left \{{r\in \mathfrak{L}_0 \;:\; \|r-r_*\|_\infty \lt \varepsilon s_n}\right \}. \end{align*}
Then
We begin by observing that the vector
![]() $\hat{\rho }_{\boldsymbol{\sigma }}$
is asymptotically normal given
$\hat{\rho }_{\boldsymbol{\sigma }}$
is asymptotically normal given
![]() $\mathfrak{A}$
. As before we let
$\mathfrak{A}$
. As before we let
![]() ${\boldsymbol{I}}_{(q-1)\times (q-1)}$
the
${\boldsymbol{I}}_{(q-1)\times (q-1)}$
the
![]() $(q-1)\times (q-1)$
-identity matrix and let
$(q-1)\times (q-1)$
-identity matrix and let
![]() ${\boldsymbol{N}}\in{\mathbb{R}}^{\mathbb{F}_q^*}$
be a Gaussian vector with zero mean and covariance matrix
${\boldsymbol{N}}\in{\mathbb{R}}^{\mathbb{F}_q^*}$
be a Gaussian vector with zero mean and covariance matrix
Claim A.1.
There exists a function
![]() $\iota =\iota (n,q)=o(1)$
such that for all axis-aligned cubes
$\iota =\iota (n,q)=o(1)$
such that for all axis-aligned cubes
![]() $U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
$U\subseteq{\mathbb{R}}^{\mathbb{F}_q^*}$
we have
Proof. Given
![]() $\mathfrak{A}$
, the mean of
$\mathfrak{A}$
, the mean of
![]() $\hat{\rho }_{\boldsymbol{\sigma }}(\tau )$
clearly equals
$\hat{\rho }_{\boldsymbol{\sigma }}(\tau )$
clearly equals
![]() $\Delta/q$
for every
$\Delta/q$
for every
![]() $\tau \in \mathbb{F}_q^*$
. Concerning the covariance matrix, for distinct
$\tau \in \mathbb{F}_q^*$
. Concerning the covariance matrix, for distinct
![]() $s\neq t$
we obtain
$s\neq t$
we obtain
 \begin{align*} \mathbb{E}_{\mathfrak{A}}[\hat{\rho }_{\boldsymbol{\sigma }}^2(s)]&=\sum _{i,j\in [n]:i\neq j}\frac{d_id_j}{q^2}+\sum _{i=1}^n\frac{d_i^2}q=\sum _{i,j=1}^n\frac{d_id_j}{q^2}+\sum _{i=1}^n\frac{d_i^2}q\left ({1-\frac 1q}\right ),\\[5pt] \mathbb{E}_{\mathfrak{A}}[\hat{\rho }_{\boldsymbol{\sigma }}(s)\hat{\rho }_{\boldsymbol{\sigma }}(t)]&=\sum _{i,j\in [n]:i\neq j}\frac{d_id_j}{q^2}=\sum _{i,j=1}^n\frac{d_id_j}{q^2}-\sum _{i=1}^n\frac{d_i^2}{q^2}. \end{align*}
\begin{align*} \mathbb{E}_{\mathfrak{A}}[\hat{\rho }_{\boldsymbol{\sigma }}^2(s)]&=\sum _{i,j\in [n]:i\neq j}\frac{d_id_j}{q^2}+\sum _{i=1}^n\frac{d_i^2}q=\sum _{i,j=1}^n\frac{d_id_j}{q^2}+\sum _{i=1}^n\frac{d_i^2}q\left ({1-\frac 1q}\right ),\\[5pt] \mathbb{E}_{\mathfrak{A}}[\hat{\rho }_{\boldsymbol{\sigma }}(s)\hat{\rho }_{\boldsymbol{\sigma }}(t)]&=\sum _{i,j\in [n]:i\neq j}\frac{d_id_j}{q^2}=\sum _{i,j=1}^n\frac{d_id_j}{q^2}-\sum _{i=1}^n\frac{d_i^2}{q^2}. \end{align*}
Hence, the means and covariances of
![]() $(\hat{\rho }_{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}})/s_n$
and
$(\hat{\rho }_{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}})/s_n$
and
![]() ${\boldsymbol{N}}$
match.
${\boldsymbol{N}}$
match.
We are thus left to prove that
![]() $(\hat{\rho }_{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}})/s_n$
is asymptotically normal, with the required uniformity. Thus, given a small
$(\hat{\rho }_{\boldsymbol{\sigma }}-q^{-1}\Delta {\mathbb{1}})/s_n$
is asymptotically normal, with the required uniformity. Thus, given a small
![]() $\iota \gt 0$
we pick
$\iota \gt 0$
we pick
![]() $D_1=D_1(q,\iota )\gt 0$
and
$D_1=D_1(q,\iota )\gt 0$
and
![]() $n_0=n_0(D_1)$
sufficiently large. Suppose
$n_0=n_0(D_1)$
sufficiently large. Suppose
![]() $n\gt n_0$
and let
$n\gt n_0$
and let
 \begin{align*} d'_{\!\!i}&={\mathbb{1}}\{d_i\leq D_1\}d_i,&d''_{\!\!\!i}&=d_i-d'_{\!\!i},\\[5pt] \hat{\rho }'_{\!\!\boldsymbol{\sigma }}(s)&=\sum _{i=1}^n{\mathbb{1}}\{\boldsymbol{\sigma }_i=s\}d'_{\!\!i},& \hat{\rho }''_{\!\!\!\boldsymbol{\sigma }}(s)&=\sum _{i=1}^n{\mathbb{1}}\{\boldsymbol{\sigma }_i=s\}d''_{\!\!\!i},\\[5pt] {s'_{\!\!n}}^2&=\sum _{i=1}^n{d'_{\!\!i}}^2,&{s''_{\!\!\!n}}^2&=\sum _{i=1}^n{d''_{\!\!\!i}}^2,\\[5pt] \Delta '&=\sum _{i=1}^n d'_{\!\!i},&\Delta ''&=\sum _{i=1}^n d''_{\!\!\!i}. \end{align*}
\begin{align*} d'_{\!\!i}&={\mathbb{1}}\{d_i\leq D_1\}d_i,&d''_{\!\!\!i}&=d_i-d'_{\!\!i},\\[5pt] \hat{\rho }'_{\!\!\boldsymbol{\sigma }}(s)&=\sum _{i=1}^n{\mathbb{1}}\{\boldsymbol{\sigma }_i=s\}d'_{\!\!i},& \hat{\rho }''_{\!\!\!\boldsymbol{\sigma }}(s)&=\sum _{i=1}^n{\mathbb{1}}\{\boldsymbol{\sigma }_i=s\}d''_{\!\!\!i},\\[5pt] {s'_{\!\!n}}^2&=\sum _{i=1}^n{d'_{\!\!i}}^2,&{s''_{\!\!\!n}}^2&=\sum _{i=1}^n{d''_{\!\!\!i}}^2,\\[5pt] \Delta '&=\sum _{i=1}^n d'_{\!\!i},&\Delta ''&=\sum _{i=1}^n d''_{\!\!\!i}. \end{align*}
By construction, we have
![]() $\Delta =\Delta '+\Delta ''$
,
$\Delta =\Delta '+\Delta ''$
,
![]() $s_n^2={s'_{\!\!n}}^2+{s''_{\!\!\!n}}^2$
as well as
$s_n^2={s'_{\!\!n}}^2+{s''_{\!\!\!n}}^2$
as well as
![]() ${s'_{\!\!n}}^2\lt D_1^2n$
. Moreover, by (P3) and (P4), both the sequences
${s'_{\!\!n}}^2\lt D_1^2n$
. Moreover, by (P3) and (P4), both the sequences
![]() $({\boldsymbol{d}}_n)_n$
and
$({\boldsymbol{d}}_n)_n$
and
![]() $({\boldsymbol{d}}^2_n)_n$
are uniformly integrable, such that for
$({\boldsymbol{d}}^2_n)_n$
are uniformly integrable, such that for
![]() $n$
large enough,
$n$
large enough,
also provided that
![]() $D_1$
is large enough. Hence, the multivariate Berry–Esseen theorem (e.g. [Reference Raič45]) shows that w.h.p. for all
$D_1$
is large enough. Hence, the multivariate Berry–Esseen theorem (e.g. [Reference Raič45]) shows that w.h.p. for all
![]() $U$
,
$U$
,
Furthermore, combining (A.3) with Chebyshev’s inequality, we see that w.h.p.
Thus, combining (A.4) and (A.5), we conclude that w.h.p.
Finally, the assertion follows from (A.6) by taking the limit
![]() $\iota \to 0$
slowly enough as
$\iota \to 0$
slowly enough as
![]() $n\to \infty$
.
$n\to \infty$
.
Let
![]() $\mathfrak{d} = \gcd ({\text{supp}}({\boldsymbol{d}}))$
, where
$\mathfrak{d} = \gcd ({\text{supp}}({\boldsymbol{d}}))$
, where
![]() ${\boldsymbol{d}}$
is the weak limit of
${\boldsymbol{d}}$
is the weak limit of
![]() $({\boldsymbol{d}}_n)_n$
. Then there exist
$({\boldsymbol{d}}_n)_n$
. Then there exist
![]() $g \in \mathbb{N}$
,
$g \in \mathbb{N}$
,
![]() $a_1, \ldots, a_g \in \mathbb{Z}$
and
$a_1, \ldots, a_g \in \mathbb{Z}$
and
![]() $\delta _1, \ldots, \delta _g$
in the support of
$\delta _1, \ldots, \delta _g$
in the support of
![]() ${\boldsymbol{d}}$
such that the greatest common divisor of the support can be linearly combined as
${\boldsymbol{d}}$
such that the greatest common divisor of the support can be linearly combined as
 \begin{align} \mathfrak{d} = \sum _{i=1}^g a_i \delta _i. \end{align}
\begin{align} \mathfrak{d} = \sum _{i=1}^g a_i \delta _i. \end{align}
We next count how many variables there are with degree
![]() $\delta _i$
. For
$\delta _i$
. For
![]() $i \in [g]$
, let
$i \in [g]$
, let
![]() $\mathfrak{I}_i$
denote the set of all
$\mathfrak{I}_i$
denote the set of all
![]() $j \in [n]$
with
$j \in [n]$
with
![]() $d_j=\delta _i$
(the set of all variables that appear in
$d_j=\delta _i$
(the set of all variables that appear in
![]() $\delta _i$
equations). Set
$\delta _i$
equations). Set
![]() $\mathfrak{I}_0 = [n] \setminus \left ({\mathfrak{I}_1 \cup \ldots \cup \mathfrak{I}_g}\right )$
. Then
$\mathfrak{I}_0 = [n] \setminus \left ({\mathfrak{I}_1 \cup \ldots \cup \mathfrak{I}_g}\right )$
. Then
and
![]() $|\mathfrak{I}_1|, \ldots, |\mathfrak{I}_g|=\Theta (n)$
because of assumption (P1). We further count how many entries of value
$|\mathfrak{I}_1|, \ldots, |\mathfrak{I}_g|=\Theta (n)$
because of assumption (P1). We further count how many entries of value
![]() $s \in \mathbb{F}_q^{\ast }$
all variables of degree
$s \in \mathbb{F}_q^{\ast }$
all variables of degree
![]() $\delta _i$
generate under the assignment
$\delta _i$
generate under the assignment
![]() $\boldsymbol{\sigma }$
, and the contribution from the rest, yielding
$\boldsymbol{\sigma }$
, and the contribution from the rest, yielding
Then summing the contributions, we get back
![]() $\hat{\rho }_{\boldsymbol{\sigma }}={\boldsymbol{r}}_0 + \sum _{i=1}^g \delta _i {\boldsymbol{r}}_i$
, where
$\hat{\rho }_{\boldsymbol{\sigma }}={\boldsymbol{r}}_0 + \sum _{i=1}^g \delta _i {\boldsymbol{r}}_i$
, where
![]() ${\boldsymbol{r}}_i=({\boldsymbol{r}}_i(s))_{s\in \mathbb{F}_q^*}$
.
${\boldsymbol{r}}_i=({\boldsymbol{r}}_i(s))_{s\in \mathbb{F}_q^*}$
.
Because
![]() $\boldsymbol{\sigma }_1, \ldots, \boldsymbol{\sigma }_n$
are mutually independent given
$\boldsymbol{\sigma }_1, \ldots, \boldsymbol{\sigma }_n$
are mutually independent given
![]() $\mathfrak{A}$
, so are
$\mathfrak{A}$
, so are
![]() ${\boldsymbol{r}}_0, {\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
. Moreover, given
${\boldsymbol{r}}_0, {\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
. Moreover, given
![]() $\mathfrak{A}$
, for
$\mathfrak{A}$
, for
![]() $i \in [g]$
,
$i \in [g]$
,
![]() ${\boldsymbol{r}}_i$
has a multinomial distribution with parameter
${\boldsymbol{r}}_i$
has a multinomial distribution with parameter
![]() $|\mathfrak{I}_i|$
and uniform probabilities
$|\mathfrak{I}_i|$
and uniform probabilities
![]() $q^{-1}$
. In effect, the individual entries
$q^{-1}$
. In effect, the individual entries
![]() ${\boldsymbol{r}}_i(s)$
,
${\boldsymbol{r}}_i(s)$
,
![]() $s \in \mathbb{F}_q^{\ast }$
, will typically differ by only a few standard deviations, that is, their typical difference will be of order
$s \in \mathbb{F}_q^{\ast }$
, will typically differ by only a few standard deviations, that is, their typical difference will be of order
![]() $O(\sqrt{|\mathfrak{I}_i|})$
. We require a precise quantitative version of this statement.
$O(\sqrt{|\mathfrak{I}_i|})$
. We require a precise quantitative version of this statement.
Furthermore, we say that
![]() ${\boldsymbol{r}}_i$
is
${\boldsymbol{r}}_i$
is
![]() $t$
-tame if
$t$
-tame if
![]() $|{\boldsymbol{r}}_i(s)-q^{-1}|\mathfrak{I}_i||\leq t\sqrt{|\mathfrak{I}_i|}$
for all
$|{\boldsymbol{r}}_i(s)-q^{-1}|\mathfrak{I}_i||\leq t\sqrt{|\mathfrak{I}_i|}$
for all
![]() $s \in \mathbb{F}_q^\ast$
. Let
$s \in \mathbb{F}_q^\ast$
. Let
![]() $\mathfrak{T}(t)$
be the event that
$\mathfrak{T}(t)$
be the event that
![]() ${\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
are
${\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
are
![]() $t$
-tame.
$t$
-tame.
Lemma A.2.
W.h.p. for every
![]() $r_*\in \mathfrak{L}_0$
there exists
$r_*\in \mathfrak{L}_0$
there exists
![]() $r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
such that
$r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
such that
Proof. Since
![]() $ {\boldsymbol{r}}_i$
has a multinomial distribution given
$ {\boldsymbol{r}}_i$
has a multinomial distribution given
![]() $\mathfrak{A}$
the Chernoff bound shows that for a large enough
$\mathfrak{A}$
the Chernoff bound shows that for a large enough
![]() $c=c(q)$
w.h.p.
$c=c(q)$
w.h.p.
Further, Claim A.1 implies that w.h.p.
![]() ${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack \geq \Omega _\varepsilon (\varepsilon ^{q-1})\geq \varepsilon ^q$
, provided
${\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack \geq \Omega _\varepsilon (\varepsilon ^{q-1})\geq \varepsilon ^q$
, provided
![]() $\varepsilon \lt \varepsilon _0=\varepsilon _0(\omega )$
is small enough. Combining this estimate with (A.9) and Bayes’ formula, we conclude that w.h.p. for every
$\varepsilon \lt \varepsilon _0=\varepsilon _0(\omega )$
is small enough. Combining this estimate with (A.9) and Bayes’ formula, we conclude that w.h.p. for every
![]() $r_*\in \mathfrak{L}_0$
,
$r_*\in \mathfrak{L}_0$
,
To complete the proof, assume that there does not exist
![]() $r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
that satisfies (A.8). Then for every
$r^*\in \mathfrak{L}_0(r_*,\varepsilon )$
that satisfies (A.8). Then for every
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
we either have
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
we either have
Let
![]() $\mathfrak{X}_0$
be the set of all
$\mathfrak{X}_0$
be the set of all
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
for which (A.11) holds, and let
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
for which (A.11) holds, and let
![]() $\mathfrak{X}_1=\mathfrak{L}_0(r_*,\varepsilon )\setminus \mathfrak{X}_0$
. Then (A.11)–(A.12) yield
$\mathfrak{X}_1=\mathfrak{L}_0(r_*,\varepsilon )\setminus \mathfrak{X}_0$
. Then (A.11)–(A.12) yield
 \begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_0}\right \rbrack +\sum _{r\in \mathfrak{X}_1}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon ) \vert \hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack }{{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack }}\\[5pt] &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_0}\right \rbrack +(1-\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_1}\right \rbrack }{{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack }}\lt 1-\varepsilon ^4, \end{align*}
\begin{align*}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_0}\right \rbrack +\sum _{r\in \mathfrak{X}_1}{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-\log \varepsilon ) \vert \hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack }{{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack }}\\[5pt] &\leq \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_0}\right \rbrack +(1-\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{X}_1}\right \rbrack }{{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r_*,\varepsilon )}\right \rbrack }}\lt 1-\varepsilon ^4, \end{align*}
provided that
![]() $1-\varepsilon ^4\gt \frac{1}{2}$
, in contradiction to (A.10).
$1-\varepsilon ^4\gt \frac{1}{2}$
, in contradiction to (A.10).
Also let
![]() $\mathfrak{T}(r,t)$
be the event that
$\mathfrak{T}(r,t)$
be the event that
![]() $\hat{\rho }_{\boldsymbol{\sigma }}=r$
and that
$\hat{\rho }_{\boldsymbol{\sigma }}=r$
and that
![]() ${\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
are
${\boldsymbol{r}}_1, \ldots, {\boldsymbol{r}}_g$
are
![]() $t$
-tame. We write
$t$
-tame. We write
![]() $(r_0, \ldots, r_g)\in \mathfrak{T}(r,t)$
if
$(r_0, \ldots, r_g)\in \mathfrak{T}(r,t)$
if
![]() $r_0 + \sum _{i=1}^g \delta _i r_i =r$
and
$r_0 + \sum _{i=1}^g \delta _i r_i =r$
and
![]() $|r_i(s)-q^{-1}|\mathfrak{I}_i||\leq t\sqrt{|\mathfrak{I}_i|}$
for all
$|r_i(s)-q^{-1}|\mathfrak{I}_i||\leq t\sqrt{|\mathfrak{I}_i|}$
for all
![]() $s \in \mathbb{F}_q^\ast$
. The following lemma summarises the key step of the proof of Lemma 7.10.
$s \in \mathbb{F}_q^\ast$
. The following lemma summarises the key step of the proof of Lemma 7.10.
Lemma A.3.
W.h.p. for any
![]() $r_*\in \mathfrak{L}_0$
, any
$r_*\in \mathfrak{L}_0$
, any
![]() $1\leq t\leq \log n$
and any
$1\leq t\leq \log n$
and any
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
there exists a one-to-one map
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
there exists a one-to-one map
![]() $\psi \;:\; \mathfrak{T}(r,t)\to \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
such that for all
$\psi \;:\; \mathfrak{T}(r,t)\to \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
such that for all
![]() $(r_0, \ldots, r_g)\in \mathfrak{T}(r,t)$
we have
$(r_0, \ldots, r_g)\in \mathfrak{T}(r,t)$
we have
Proof. Since
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
, thanks to assumption (P7), we have
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
, thanks to assumption (P7), we have
![]() $r-r'\in \mathfrak{d} \mathbb{Z}^{\mathbb{F}_q^\ast }$
. Hence, with
$r-r'\in \mathfrak{d} \mathbb{Z}^{\mathbb{F}_q^\ast }$
. Hence, with
![]() $e_1, \ldots, e_{q-1}$
denoting the standard basis of
$e_1, \ldots, e_{q-1}$
denoting the standard basis of
![]() ${\mathbb{R}}^{\mathbb{F}_q^{\ast }}$
, there is a unique representation
${\mathbb{R}}^{\mathbb{F}_q^{\ast }}$
, there is a unique representation
 \begin{align} r'-r&=\sum _{i=1}^{q-1}\lambda _i\mathfrak{d} e_i \end{align}
\begin{align} r'-r&=\sum _{i=1}^{q-1}\lambda _i\mathfrak{d} e_i \end{align}
with
![]() $\lambda _1, \ldots, \lambda _{q-1} \in \mathbb{Z}$
. Because
$\lambda _1, \ldots, \lambda _{q-1} \in \mathbb{Z}$
. Because
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
and
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
and
 \begin{align*} \lambda \;:\!=\;\begin{pmatrix}\lambda _1\\[5pt] \vdots \\[5pt] \lambda _{q-1}\end{pmatrix}=\mathfrak{d}^{-1}(r'-r), \end{align*}
\begin{align*} \lambda \;:\!=\;\begin{pmatrix}\lambda _1\\[5pt] \vdots \\[5pt] \lambda _{q-1}\end{pmatrix}=\mathfrak{d}^{-1}(r'-r), \end{align*}
the coefficients satisfy
Now recall
![]() $g \in \mathbb{N}$
,
$g \in \mathbb{N}$
,
![]() $a_1, \ldots, a_g \in \mathbb{Z}$
and
$a_1, \ldots, a_g \in \mathbb{Z}$
and
![]() $\delta _1, \ldots, \delta _g$
in the support of
$\delta _1, \ldots, \delta _g$
in the support of
![]() ${\boldsymbol{d}}$
with
${\boldsymbol{d}}$
with
 \begin{align*} \mathfrak{d} = \sum _{i=1}^g a_i \delta _i. \end{align*}
\begin{align*} \mathfrak{d} = \sum _{i=1}^g a_i \delta _i. \end{align*}
Fir
![]() $i \in [g]$
, we set
$i \in [g]$
, we set
as well as
![]() $ r_0' = r_0$
. Further, define
$ r_0' = r_0$
. Further, define
![]() $\psi (r_0, \ldots, r_g)=(r_0', \ldots, r'_{\!\!g})$
. Then clearly
$\psi (r_0, \ldots, r_g)=(r_0', \ldots, r'_{\!\!g})$
. Then clearly
 \begin{align} r_0 + \sum _{i=1}^g \delta _i r'_{\!\!i} = r + \sum _{i=1}^g \frac{a_i \delta _i}{\mathfrak{d}} \lambda = r + r' - r =r'. \end{align}
\begin{align} r_0 + \sum _{i=1}^g \delta _i r'_{\!\!i} = r + \sum _{i=1}^g \frac{a_i \delta _i}{\mathfrak{d}} \lambda = r + r' - r =r'. \end{align}
and due to (A.15), we have
![]() $\psi (r_0,\ldots,r_g)\in \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
. Finally, for
$\psi (r_0,\ldots,r_g)\in \mathfrak{T}(r',t+O_\varepsilon (\varepsilon ))$
. Finally, for
![]() $i \in [g]$
set
$i \in [g]$
set
Moreover, Stirling’s formula and the mean value theorem show that
 \begin{align}& \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{r}}_0,\ldots,{\boldsymbol{r}}_g)=(r_0, \ldots, r_g)}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{r}}_0, \ldots,{\boldsymbol{r}}_g)=\psi (r_0, \ldots, r_g)}\right \rbrack }\nonumber \\[5pt] &=\frac{\binom{|\mathfrak{I}_1|}{(r_1(0), r_1)} \cdot \ldots \cdot \binom{|\mathfrak{I}_g|}{ (r_g(0), r_g) }}{\binom{|\mathfrak{I}_1|}{(r'_{\!\!1}(0),r'_{\!\!1})} \cdot \ldots \cdot \binom{|\mathfrak{I}_g|}{(r'_{\!\!g}(0), r'_{\!\!g})} }=\exp\!\left \lbrack{\sum _{i=1}^g\sum _{s \in \mathbb{F}_q}O_\varepsilon \left ({r'_{\!\!i}(s)\log r'_{\!\!i}(s)-r_i(s)\log r_i(s)}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{\sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q}\left |{\int _{r_i(s)/|\mathfrak{I}_i|}^{r'_{\!\!i}(s)/|\mathfrak{I}_i|}\log z{\text{d}} z}\right |}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{\sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q} \left ({\frac{r'_{\!\!i}(s)}{|\mathfrak{I}_i|}-\frac{r_i(s)}{|\mathfrak{I}_i|}}\right )\log \left ({\frac 1q+O_\varepsilon \left ({\frac{(\omega +t)s_n}{|\mathfrak{I}_i|}}\right )}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{ \sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q} O_\varepsilon \left ({\frac{(\omega +t)s_n}{|\mathfrak{I}_i|}\left ({\frac{r'_{\!\!i}(s)}{|\mathfrak{I}_i|}-\frac{r_i(s)}{|\mathfrak{I}_i|}}\right )}\right )}\right \rbrack . \end{align}
\begin{align}& \frac{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{r}}_0,\ldots,{\boldsymbol{r}}_g)=(r_0, \ldots, r_g)}\right \rbrack }{{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{({\boldsymbol{r}}_0, \ldots,{\boldsymbol{r}}_g)=\psi (r_0, \ldots, r_g)}\right \rbrack }\nonumber \\[5pt] &=\frac{\binom{|\mathfrak{I}_1|}{(r_1(0), r_1)} \cdot \ldots \cdot \binom{|\mathfrak{I}_g|}{ (r_g(0), r_g) }}{\binom{|\mathfrak{I}_1|}{(r'_{\!\!1}(0),r'_{\!\!1})} \cdot \ldots \cdot \binom{|\mathfrak{I}_g|}{(r'_{\!\!g}(0), r'_{\!\!g})} }=\exp\!\left \lbrack{\sum _{i=1}^g\sum _{s \in \mathbb{F}_q}O_\varepsilon \left ({r'_{\!\!i}(s)\log r'_{\!\!i}(s)-r_i(s)\log r_i(s)}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{\sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q}\left |{\int _{r_i(s)/|\mathfrak{I}_i|}^{r'_{\!\!i}(s)/|\mathfrak{I}_i|}\log z{\text{d}} z}\right |}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{\sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q} \left ({\frac{r'_{\!\!i}(s)}{|\mathfrak{I}_i|}-\frac{r_i(s)}{|\mathfrak{I}_i|}}\right )\log \left ({\frac 1q+O_\varepsilon \left ({\frac{(\omega +t)s_n}{|\mathfrak{I}_i|}}\right )}\right )}\right \rbrack \nonumber \\[5pt] &=\exp\!\left \lbrack{ \sum _{i=1}^gO_\varepsilon (|\mathfrak{I}_i|)\sum _{s \in \mathbb{F}_q} O_\varepsilon \left ({\frac{(\omega +t)s_n}{|\mathfrak{I}_i|}\left ({\frac{r'_{\!\!i}(s)}{|\mathfrak{I}_i|}-\frac{r_i(s)}{|\mathfrak{I}_i|}}\right )}\right )}\right \rbrack . \end{align}
Since
![]() $|\mathfrak{I}_1|, \ldots, |\mathfrak{I}_g|=\Theta _\varepsilon (n)$
, (A.17) implies (A.13). Finally,
$|\mathfrak{I}_1|, \ldots, |\mathfrak{I}_g|=\Theta _\varepsilon (n)$
, (A.17) implies (A.13). Finally,
![]() $\psi$
is one to one because each vector has a unique representation with respect to the basis
$\psi$
is one to one because each vector has a unique representation with respect to the basis
![]() $(e_1,\ldots,e_{q-1})$
.
$(e_1,\ldots,e_{q-1})$
.
Roughly speaking, LemmaA.3 shows that any two tame
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
close to a conceivable
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
close to a conceivable
![]() $r_*\in \mathfrak{L}_0$
are about equally likely. However, the map
$r_*\in \mathfrak{L}_0$
are about equally likely. However, the map
![]() $\psi$
produces solutions that are a little less tame than the ones we start from. The following corollary, which combines Lemmas 7.14 and 7.15, remedies this issue.
$\psi$
produces solutions that are a little less tame than the ones we start from. The following corollary, which combines Lemmas 7.14 and 7.15, remedies this issue.
Corollary A.4.
W.h.p. for all
![]() $r_*\in \mathfrak{L}_0$
and all
$r_*\in \mathfrak{L}_0$
and all
![]() $r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
we have
$r,r'\in \mathfrak{L}_0(r_*,\varepsilon )$
we have
Proof. Let
![]() $r^*$
be the vector supplied by Lemma A.2. Applying Lemma A.3 to
$r^*$
be the vector supplied by Lemma A.2. Applying Lemma A.3 to
![]() $r^*$
and
$r^*$
and
![]() $r\in \mathfrak{L}_0(r_*,\varepsilon )$
, we see that w.h.p.
$r\in \mathfrak{L}_0(r_*,\varepsilon )$
, we see that w.h.p.
In addition, we claim that w.h.p.
Indeed, applying Lemma 7.15 twice to
![]() $r$
and
$r$
and
![]() $r^*$
and invoking (7.26), we see that w.h.p.
$r^*$
and invoking (7.26), we see that w.h.p.
 \begin{align} \nonumber{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )}\right \rbrack &\geq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )}\right \rbrack \\[5pt] &\geq \left ({1-O_\varepsilon (\varepsilon \log \varepsilon )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r^*}\right \rbrack, \end{align}
\begin{align} \nonumber{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-2\log \varepsilon )}\right \rbrack &\geq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )}\right \rbrack \\[5pt] &\geq \left ({1-O_\varepsilon (\varepsilon \log \varepsilon )}\right ){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r^*}\right \rbrack, \end{align}
 \begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-4\log \varepsilon )\setminus \mathfrak{T}(r,-3\log \varepsilon )}\right \rbrack &\leq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\setminus \mathfrak{T}(r^*,-2\log \varepsilon )}\right \rbrack \nonumber \\[5pt] O_\varepsilon (\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r^*}\right \rbrack . \end{align}
\begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r,-4\log \varepsilon )\setminus \mathfrak{T}(r,-3\log \varepsilon )}\right \rbrack &\leq \exp\!(O_\varepsilon (\varepsilon \log \varepsilon )){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(r^*,-3\log \varepsilon )\setminus \mathfrak{T}(r^*,-2\log \varepsilon )}\right \rbrack \nonumber \\[5pt] O_\varepsilon (\varepsilon ^4){\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r^*}\right \rbrack . \end{align}
Combining (A.20) and (A.21) yields (A.19).
Finally, (7.26), (A.18) and (A.19) show that w.h.p.
 \begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack \geq 1-\sqrt \varepsilon,\nonumber \\[5pt] &{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}=r'}\right \rbrack \geq 1-\sqrt \varepsilon \qquad \mbox{for all }r,r'\in \mathfrak{L}_0(r_*,\varepsilon ), \end{align}
\begin{align} & {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack \geq 1-\sqrt \varepsilon,\nonumber \\[5pt] &{\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\mathfrak{T}(-3\log \varepsilon )\mid \hat{\rho }_{\boldsymbol{\sigma }}=r'}\right \rbrack \geq 1-\sqrt \varepsilon \qquad \mbox{for all }r,r'\in \mathfrak{L}_0(r_*,\varepsilon ), \end{align}
Proof of Claim
7.17. Claim A.1 shows that for any
![]() $r\in \mathfrak{L}_0$
and
$r\in \mathfrak{L}_0$
and
![]() $\textbf{N} \sim \mathcal{N}(0, \mathcal C)$
$\textbf{N} \sim \mathcal{N}(0, \mathcal C)$
Moreover, Corollary A.4 implies that given
![]() $\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r,\varepsilon )$
,
$\hat{\rho }_{\boldsymbol{\sigma }}\in \mathfrak{L}_0(r,\varepsilon )$
,
![]() $\hat{\rho }_{\boldsymbol{\sigma }}$
is within
$\hat{\rho }_{\boldsymbol{\sigma }}$
is within
![]() $o_\varepsilon (1)$
of the uniform distribution on
$o_\varepsilon (1)$
of the uniform distribution on
![]() $\mathfrak{L}_0(r,\varepsilon )$
. Furthermore, Lemma 3.6 applied to the module
$\mathfrak{L}_0(r,\varepsilon )$
. Furthermore, Lemma 3.6 applied to the module
![]() $\mathfrak{M} = \mathfrak{d} \mathbb{Z}^{\mathbb{F}_q^\ast }$
with basis
$\mathfrak{M} = \mathfrak{d} \mathbb{Z}^{\mathbb{F}_q^\ast }$
with basis
![]() $\{\mathfrak{d} e_1, \ldots, \mathfrak{d} e_{q-1}\}$
shows that the number of points in
$\{\mathfrak{d} e_1, \ldots, \mathfrak{d} e_{q-1}\}$
shows that the number of points in
![]() $\mathfrak{L}_0(r,\varepsilon )$
satisfies
$\mathfrak{L}_0(r,\varepsilon )$
satisfies
Finally, the eigenvalues of the matrix
![]() $\mathcal{C}$
are
$\mathcal{C}$
are
![]() $q^{-2}$
(once) and
$q^{-2}$
(once) and
![]() $q^{-1}$
(
$q^{-1}$
(
![]() $(q-2)$
times). Hence,
$(q-2)$
times). Hence,
![]() $\det \mathcal{C}=q^{-q}$
. Therefore, w.h.p. for all
$\det \mathcal{C}=q^{-q}$
. Therefore, w.h.p. for all
![]() $r\in \mathfrak{L}_0$
we have
$r\in \mathfrak{L}_0$
we have
 \begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack &=(1+o_\varepsilon (1))\frac{q^{q/2}\mathfrak{d}^{q-1}}{(2\pi{\Delta _2} )^{(q-1)/2}} \exp\!\left \lbrack{-\frac{(r-q^{-1}\Delta {\mathbb{1}})^T\mathcal C^{-1}(r-q^{-1}\Delta {\mathbb{1}})}{2{\Delta _2}}}\right \rbrack . \end{align}
\begin{align} {\mathbb{P}}_{\mathfrak{A}}\left \lbrack{\hat{\rho }_{\boldsymbol{\sigma }}=r}\right \rbrack &=(1+o_\varepsilon (1))\frac{q^{q/2}\mathfrak{d}^{q-1}}{(2\pi{\Delta _2} )^{(q-1)/2}} \exp\!\left \lbrack{-\frac{(r-q^{-1}\Delta {\mathbb{1}})^T\mathcal C^{-1}(r-q^{-1}\Delta {\mathbb{1}})}{2{\Delta _2}}}\right \rbrack . \end{align}