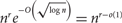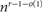Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gerbner, Dániel
and
Patkós, Balázs
2022.
Generalized Turán Problems for Complete Bipartite Graphs.
Graphs and Combinatorics,
Vol. 38,
Issue. 5,
Balogh, József
Delcourt, Michelle
Heath, Emily
and
Li, Lina
2022.
Generalized rainbow Turán numbers of odd cycles.
Discrete Mathematics,
Vol. 345,
Issue. 2,
p.
112663.
Gerbner, Dániel
and
Patkós, Balázs
2024.
Generalized Turán results for intersecting cliques.
Discrete Mathematics,
Vol. 347,
Issue. 1,
p.
113710.
Kovács, Benedek
and
Nagy, Zoltán Lóránt
2024.
Multicolor Turán numbers II: A generalization of the Ruzsa–Szemerédi theorem and new results on cliques and odd cycles.
Journal of Graph Theory,
Vol. 107,
Issue. 3,
p.
629.
Chakraborti, Debsoumya
Hendrey, Kevin
Lund, Ben
and
Tompkins, Casey
2024.
Rainbow Saturation for Complete Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 38,
Issue. 1,
p.
1090.
Bhattacharya, Bhaswar B.
Das, Sandip
Samim Islam, Sk
and
Sen, Saumya
2026.
Growth rates of the number of empty triangles and simplices.
Computational Geometry,
Vol. 130,
Issue. ,
p.
102197.