Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T23:23:19.539Z Has data issue: false hasContentIssue false
  • English
  • Français

Hamiltonian Berge cycles in random hypergraphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  08 September 2020

Deepak Bal ,
Ross Berkowitz ,
Pat Devlin  and
Mathias Schacht
Deepak Bal
Affiliation:
Department of Mathematics, Montclair State University, Montclair, NJ 07043, USA
Ross Berkowitz
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, USA
Pat Devlin*
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, USA
Mathias Schacht
Affiliation:
Department of Mathematics, University of Hamburg, 20146 Hamburg, Germany
*
*Corresponding author. Email: patrick.devlin@yale.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note we study the emergence of Hamiltonian Berge cycles in random r-uniform hypergraphs. For 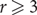$r\geq 3$ we prove an optimal stopping time result that if edges are sequentially added to an initially empty r-graph, then as soon as the minimum degree is at least 2, the hypergraph with high probability has such a cycle. In particular, this determines the threshold probability for Berge Hamiltonicity of the Erdős–Rényi random r-graph, and we also show that the 2-out random r-graph with high probability has such a cycle. We obtain similar results for weak Berge cycles as well, thus resolving a conjecture of Poole.

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05C45: Eulerian and Hamiltonian graphs 05C80: Random graphs 05C38: Paths and cycles 05D40: Probabilistic methods 05C20: Directed graphs (digraphs), tournaments
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 228 - 238
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

An earlier arXiv draft of this paper did not have our stopping time results.

References

Ajtai, M., Komlós, J. and Szemerédi, E. (1985) First occurrence of Hamilton cycles in random graphs. In Cycles in Graphs (Burnaby, BC, 1982), Vol. 115 of North-Holland Mathematics Studies, pp. 173–178. North-Holland.Google Scholar
Alon, Y. and Krivelevich, M. (2020) Random graph’s Hamiltonicity is strongly tied to its minimum degree. Electron. J. Combin. 27 P1.30.CrossRefGoogle Scholar
Berge, C. (1970) Graphes et Hypergraphes, Vol. 37 of Monographies Universitaires de Mathématiques. Dunod.Google Scholar
Bohman, T. and Frieze, A. (2009) Hamilton cycles in 3-out. Random Struct. Algorithms 35 393–417.CrossRefGoogle Scholar
Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics (Cambridge, 1983), pp. 35–57. Academic Press.Google Scholar
Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.CrossRefGoogle Scholar
Clemens, D., Ehrenmüller, J. and Person, Y. (2016) A Dirac-type theorem for Hamilton Berge cycles in random hypergraphs. Electron. Notes Discrete Math. 54 181–186.CrossRefGoogle Scholar
Cooper, C. and Frieze, A. (2000) Hamilton cycles in random graphs and directed graphs. Random Struct. Algorithms 16 369–401.3.0.CO;2-J>CrossRefGoogle Scholar
Devlin, P. and Kahn, J. (2017) Perfect fractional matchings in k-out hypergraphs. Electron. J. Combin. 24 3–60.CrossRefGoogle Scholar
Dudek, A. and Frieze, A. (2011) Loose Hamilton cycles in random uniform hypergraphs. Electron. J. Combin. 18 P48.CrossRefGoogle Scholar
Dudek, A. and Frieze, A. (2013) Tight Hamilton cycles in random uniform hypergraphs. Random Struct. Algorithms 42 374–385.CrossRefGoogle Scholar
Dudek, A. and Helenius, L. (2018) On offset Hamilton cycles in random hypergraphs. Discrete Appl. Math. 238 77–85.CrossRefGoogle Scholar
Dudek, A., Frieze, A., Loh, P.-S. and Speiss, S. (2012) Optimal divisibility conditions for loose Hamilton cycles in random hypergraphs. Electron. J. Combin. 19 P44.CrossRefGoogle Scholar
Fenner, T. I. and Frieze, A. M. (1982) On the connectivity of random m-orientable graphs and digraphs. Combinatorica 2 347–359.CrossRefGoogle Scholar
Frieze, A. and Karoński, M. (2016) Introduction to Random Graphs. Cambridge University Press.CrossRefGoogle Scholar
Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.CrossRefGoogle Scholar
Krivelevich, M. (2016) Long paths and Hamiltonicity in random graphs. In Random Graphs, Geometry and Asymptotic Structure (Krivelevich, M. et al., eds), Vol. 84 of London Mathematical Society Student Texts, pp. 4–27. Cambridge University Press.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2014) Hamilton cycles in graphs and hypergraphs: an extremal perspective. Proceedings of the International Congress of Mathematicians—Seoul 2014. Vol. IV, 381–406, Kyung Moon Sa, Seoul.Google Scholar
Parczyk, O. and Person, Y. (2016) Spanning structures and universality in sparse hypergraphs. Random Struct. Algorithms 49 819–844.CrossRefGoogle Scholar
Poole, D. (2014) On weak Hamiltonicity of a random hypergraph. arXiv:1410.7446Google Scholar