Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cairnie, Niall
and
Edwards, Keith
1998.
The achromatic number of bounded degree trees.
Discrete Mathematics,
Vol. 188,
Issue. 1-3,
p.
87.
Krysta, Piotr
and
Loryś, Krzysztof
2006.
Efficient approximation algorithms for the achromatic number.
Theoretical Computer Science,
Vol. 361,
Issue. 2-3,
p.
150.
Muntaner-Batle, Francisco Antonio
Vernold Vivin, J.
and
Venkatachalam, M.
2014.
Harmonious Coloring on Corona Product of Complete Graphs.
National Academy Science Letters,
Vol. 37,
Issue. 5,
p.
461.
Kolay, Sudeshna
Pandurangan, Ragukumar
Panolan, Fahad
Raman, Venkatesh
and
Tale, Prafullkumar
2016.
Graph-Theoretic Concepts in Computer Science.
Vol. 9941,
Issue. ,
p.
245.
Kolay, Sudeshna
Pandurangan, Ragukumar
Panolan, Fahad
Raman, Venkatesh
and
Tale, Prafullkumar
2019.
Harmonious coloring: Parameterized algorithms and upper bounds.
Theoretical Computer Science,
Vol. 772,
Issue. ,
p.
132.
Franklin Thamil Selvi, M. S
and
Amutha, A.
2021.
Optimization of Harmonious Coloring Problem in Mesh Derived Architecture.
Journal of Physics: Conference Series,
Vol. 1770,
Issue. 1,
p.
012082.

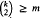 . We also give a polynomial time algorithm for determining the harmonious chromatic number of a tree with maximum degree at most
. We also give a polynomial time algorithm for determining the harmonious chromatic number of a tree with maximum degree at most 