Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T07:39:22.680Z Has data issue: false hasContentIssue false
  • English
  • Français

Independent dominating sets in graphs of girth five

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  15 October 2020

Ararat Harutyunyan ,
Paul Horn  and
Jacques Verstraete
Ararat Harutyunyan*
Affiliation:
LAMSADE, CNRS, Université Paris-Dauphine, PSL Research University, 75016 Paris, France
Paul Horn
Affiliation:
Department of Mathematics, University of Denver, CO 80210, USA
Jacques Verstraete
Affiliation:
Department of Mathematics, University of California at San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
*
*Corresponding author. Email: ararat.harutyunyan@dauphine.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 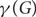$\gamma(G)$ and 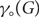$${\gamma _ \circ }(G)$$ denote the sizes of a smallest dominating set and smallest independent dominating set in a graph G, respectively. One of the first results in probabilistic combinatorics is that if G is an n-vertex graph of minimum degree at least d, then

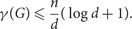$$\begin{equation}\gamma(G) \leq \frac{n}{d}(\log d + 1).\end{equation}$$

In this paper the main result is that if G is any n-vertex d-regular graph of girth at least five, then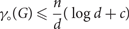

$$\begin{equation}\gamma_(G) \leq \frac{n}{d}(\log d + c)\end{equation}$$
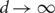for some constant c independent of d. This result is sharp in the sense that as $d \rightarrow \infty$ , almost all d-regular n-vertex graphs G of girth at least five have
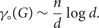$$\begin{equation}\gamma_(G) \sim \frac{n}{d}\log d.\end{equation}$$

Furthermore, if G is a disjoint union of 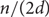${n}/{(2d)}$ complete bipartite graphs 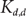$K_{d,d}$ , then 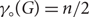${\gamma_\circ}(G) = \frac{n}{2}$ . We also prove that there are n-vertex graphs G of minimum degree d and whose maximum degree grows not much faster than d log d such that 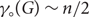${\gamma_\circ}(G) \sim {n}/{2}$ as 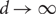$d \rightarrow \infty$ . Therefore both the girth and regularity conditions are required for the main result.

MSC classification

Primary: 05C35: Extremal problems 05C69: Dominating sets, independent sets, cliques 05C80: Random graphs 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 344 - 359
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by an Alfred P. Sloan Research Fellowship and NSF grant DMS 0800704.

References

Alon, N., Krivelevich, M. and Sudakov, B. (1999) Coloring graphs with sparse neighbourhoods. J. Combin. Theory Ser. B 77 73–82.Google Scholar
Arnautov, V. I. (1974) Estimation of the exterior stability number of a graph by means of the minimal degree of the vertices (in Russian). Prikl. Mat. i Programmirovanie 11 3–8.Google Scholar
Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
Duckworth, W. and Wormald, N. (2006) On the independent domination number of random regular graphs. Combin. Probab. Comput. 15 513–522.CrossRefGoogle Scholar
Erdös, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In Infinite and Finite Sets (Hajnal, A. et al., eds), Vol. 11 of Colloquia Mathematica Societatis János Bolyai, pp. 609–627.Google Scholar
Frieze, A. M. and Łuczak, T. (1992) On the independence and chromatic numbers of random regular graphs. J. Combin. Theory Ser. B 54 123–132.CrossRefGoogle Scholar
Gamarnik, D. and Goldberg, D. (2010) Randomized greedy algorithms for independent sets and matchings in regular graphs: exact results and finite girth corrections. Combin. Probab. Comput. 19 61–85.CrossRefGoogle Scholar
Godbole, A. and Hitczenko, P. (1998) Beyond the method of bounded differences. In Microsurveys in Discrete Probability (Princeton, NJ, 1997) (Aldous, D. and Propp, J., eds), pp. 43–58, AMS and DIMACS.Google Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.CrossRefGoogle Scholar
Johansson, A. (1996) Asymptotic choice number for triangle free graphs. DIMACS Technical Report 91-95.Google Scholar
Lauer, J. and Wormald, N. (2007) Large independent sets in regular graphs of large girth. J. Combin. Theory Ser. B 97 999–1009.Google Scholar
Lovász, L. (1975) On the ratio of optimal and integral fractional covers. Discrete Math. 13 383–390.CrossRefGoogle Scholar
McDiarmid, C. (1998) Concentration. In Probabilistic Methods for Algorithmic Discrete Mathematics, Vol. 16 of Algorithms and Combinatorics, pp. 195–248, Springer.Google Scholar
Payan, C. (1975) Sur le nombre d’absorption d’un graphe simple (in French). Proc. Colloq. Th. Graphes (Paris 1974), C.C.E.R.O 17 307–317.Google Scholar
Shearer, J. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.CrossRefGoogle Scholar
Shamir, E. and Spencer, J. (1987) Sharp concentration of the chromatic number on random graphs ${G_{n,p}}$ . Combinatorica 7 121–129.CrossRefGoogle Scholar
Wormald, N. (1999) The differential equation method for random graph processes and greedy algorithms. In Lectures on Approximation and Randomized Algorithms (Karoński, M. and Prömel, H. J., eds), pp. 73–155, PWN.Google Scholar
Zito, M. (2001) Greedy algorithms for minimisation problems in random regular graphs. In Proceedings of the 9th Annual European Symposium on Algorithms, Vol. 2161 of Lecture Notes in Computer Science, pp. 524–536, Springer.Google Scholar