Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T22:59:51.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Independent Transversals in Sparse Partite Hypergraphs

Published online by Cambridge University Press:  12 September 2008

Paul Erdős ,
András Gyárfás  and
Tomasz Łuczak
Paul Erdős
Affiliation:
Institute of Mathematics, Hungarian Academy of Sciences
András Gyárfás
Affiliation:
Computer and Automation Institute, Hungarian Academy of Sciences
Tomasz Łuczak
Affiliation:
Mathematical Institute, Polish Academy of Sciences
Get access Rights & Permissions [Opens in a new window]

Abstract

An [n, k, r]-hypergraph is a hypergraph 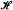= (V, E) whose vertex set V is partitioned into n k-element sets V1, V2,…, Vn and for which, for each choice of r indices, 1 ≤ i1 < i2 < … < ir ≤ n, there is exactly one edge e ∈ E such that |e∩Vi| = 1 if i ∈ {i1, i2.…, ir} and otherwise |e ∩ Vi| = 0. An independent transversal of an [n, k, r]-hypergraph is a set T = {a1, a2,…, an} ⊆ V such that ai ∈ Vi for i = 1, 2, …, n and e ⊈ T for all e ∈ E. The purpose of this note is to estimate fr(k), defined as the largest n for which any [n, k, r]-hypergraph has an independent transversal. The sharpest results are for r = 2 and for the case when k is small compared to r.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 3 , Issue 3 , September 1994 , pp. 293 - 296
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Spencer, J. (1992) The Probabilistic Method, John Wiley & Sons.Google Scholar
[2]Erdős, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In: Hajnal, A., Rado, R. and Sós, V. T. (eds.) Infinite and Finite Sets, North-Holland 609–627.Google Scholar
[3]Nešetřil, J. and Rödl, V. (1979) A short proof for the existence of Highly Chromatic Hypergraphs without short cycles. Journal of Combinatorial Th. B 27 225–227.CrossRefGoogle Scholar
[4]Yuster, R. (1994) personal communication.Google Scholar