Article contents
Irregular subgraphs
Published online by Cambridge University Press: 23 September 2022
Abstract
We suggest two related conjectures dealing with the existence of spanning irregular subgraphs of graphs. The first asserts that any 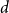 $d$-regular graph on
$d$-regular graph on  $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between
$n$ vertices contains a spanning subgraph in which the number of vertices of each degree between 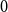 $0$ and
$0$ and 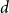 $d$ deviates from
$d$ deviates from 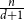 $\frac{n}{d+1}$ by at most
$\frac{n}{d+1}$ by at most 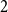 $2$. The second is that every graph on
$2$. The second is that every graph on  $n$ vertices with minimum degree
$n$ vertices with minimum degree 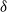 $\delta$ contains a spanning subgraph in which the number of vertices of each degree does not exceed
$\delta$ contains a spanning subgraph in which the number of vertices of each degree does not exceed 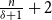 $\frac{n}{\delta +1}+2$. Both conjectures remain open, but we prove several asymptotic relaxations for graphs with a large number of vertices
$\frac{n}{\delta +1}+2$. Both conjectures remain open, but we prove several asymptotic relaxations for graphs with a large number of vertices  $n$. In particular we show that if
$n$. In particular we show that if 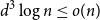 $d^3 \log n \leq o(n)$ then every
$d^3 \log n \leq o(n)$ then every 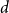 $d$-regular graph with
$d$-regular graph with  $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between
$n$ vertices contains a spanning subgraph in which the number of vertices of each degree between 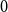 $0$ and
$0$ and 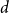 $d$ is
$d$ is 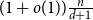 $(1+o(1))\frac{n}{d+1}$. We also prove that any graph with
$(1+o(1))\frac{n}{d+1}$. We also prove that any graph with  $n$ vertices and minimum degree
$n$ vertices and minimum degree 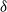 $\delta$ contains a spanning subgraph in which no degree is repeated more than
$\delta$ contains a spanning subgraph in which no degree is repeated more than 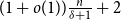 $(1+o(1))\frac{n}{\delta +1}+2$ times.
$(1+o(1))\frac{n}{\delta +1}+2$ times.
Keywords
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Research supported in part by NSF grant DMS-2154082 and BSF grant 2018267.
Research supported by NSF Award DMS-1953958.
References
- 5
- Cited by


