Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-11T00:21:51.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Large complete minors in random subgraphs

Part of: Graph theory

Published online by Cambridge University Press:  03 December 2020

Joshua Erde ,
Mihyun Kang  and
Michael Krivelevich
Joshua Erde*
Affiliation:
Institute of Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010 Graz, Austria
Mihyun Kang
Affiliation:
Institute of Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010 Graz, Austria
Michael Krivelevich
Affiliation:
School of Mathematical Sciences, Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv6997801, Israel
*
*Corresponding author. Email: erde@tugraz.at
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a graph of minimum degree at least k and let Gp be the random subgraph of G obtained by keeping each edge independently with probability p. We are interested in the size of the largest complete minor that Gp contains when p = (1 + ε)/k with ε > 0. We show that with high probability Gp contains a complete minor of order 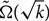$\tilde{\Omega}(\sqrt{k})$ , where the ~ hides a polylogarithmic factor. Furthermore, in the case where the order of G is also bounded above by a constant multiple of k, we show that this polylogarithmic term can be removed, giving a tight bound.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C83: Graph minors
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 4 , July 2021 , pp. 619 - 630
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by the Austrian Science Fund (FWF): I3747.

‡

Supported in part by USA–Israel BSF grant 2018267, and by ISF grant 1261/17.

References

Bollobás, B. (2001) Random Graphs, Vol. 73 of Cambridge Studies in Advanced Mathematics, second edition. Cambridge University Press.Google Scholar
Ehard, S. and Joos, F. (2018) Paths and cycles in random subgraphs of graphs with large minimum degree. Electron. J. Combin. 25 2–31.CrossRefGoogle Scholar
Fountoulakis, N., Kühn, D. and Osthus, D. (2008) The order of the largest complete minor in a random graph. Random Struct. Alg. 33 127–141.CrossRefGoogle Scholar
Frieze, A. and Karoński, M. (2016) Introduction to Random Graphs. Cambridge University Press.CrossRefGoogle Scholar
Frieze, A. and Krivelevich, M. (2013) On the non-planarity of a random subgraph. Combin. Probab. Comput. 22 722–732.CrossRefGoogle Scholar
Gilbert, E. N. (1959) Random graphs. Ann. Math. Statist. 30 1141–1144.CrossRefGoogle Scholar
Glebov, R., Naves, H. and Sudakov, B. (2017) The threshold probability for long cycles. Combin. Probab. Comput. 26 208–247.CrossRefGoogle Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58(301) 13–30.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley-Interscience.CrossRefGoogle Scholar
Kawarabayashi, K. and Reed, B. (2010) A separator theorem in minor-closed classes. In 2010 IEEE 51st Annual Symposium on Foundations of Computer Science, pp. 153–162. IEEE.CrossRefGoogle Scholar
Kostochka, A. V. (1982) The minimum Hadwiger number for graphs with a given mean degree of vertices. Metody Diskretnogo Analiza 38 37–58.Google Scholar
Kostochka, A. V. (1984) Lower bound of the Hadwiger number of graphs by their average degree. Combinatorica 4 307–316.CrossRefGoogle Scholar
Krivelevich, M. (2018) Finding and using expanders in locally sparse graphs. SIAM J. Discrete Math. 32 611–623.CrossRefGoogle Scholar
Krivelevich, M. (2019) Expanders: how to find them, and what to find in them. In Surveys in Combinatorics 2019, Vol. 456 of London Mathematical Society Lecture Note Series, pp. 115–142. Cambridge University Press.Google Scholar
Krivelevich, M., Lee, C. and Sudakov, B. (2015) Long paths and cycles in random subgraphs of graphs with large minimum degree. Random Struct. Algorithms 46 320–345.CrossRefGoogle Scholar
Krivelevich, M. and Nachmias, A. (2006) Coloring complete bipartite graphs from random lists. Random Struct. Algorithms 29 436–449.CrossRefGoogle Scholar
Krivelevich, M. and Samotij, W. (2014) Long paths and cycles in random subgraphs of $\mathcal{H}$ -free graphs. Electron. J. Combin 21 1–30.CrossRefGoogle Scholar
Krivelevich, M. and Sudakov, B. (2013) The phase transition in random graphs: a simple proof. Random Struct. Algorithms 43 131–138.CrossRefGoogle Scholar
Riordan, O. (2014) Long cycles in random subgraphs of graphs with large minimum degree. Random Struct. Algorithms 45 764–767.CrossRefGoogle Scholar
Thomason, A. (1984) An extremal function for contractions of graphs. Math. Proc. Camb. Phil. Soc. 95 261–265.CrossRefGoogle Scholar
Thomason, A. (2001) The extremal function for complete minors. J. Combin. Theory Ser. B 81 318–338.CrossRefGoogle Scholar