Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T08:41:36.752Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Turán Numbers of Linear Cycles and Cycle-Complete Ramsey Numbers

Part of: Graph theory

Published online by Cambridge University Press:  02 November 2017

CLAYTON COLLIER-CARTAINO ,
NATHAN GRABER  and
TAO JIANG
CLAYTON COLLIER-CARTAINO
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA (e-mail: colliec@miamioh.edu, jiangt@miamioh.edu)
NATHAN GRABER
Affiliation:
Department of Mathematics and Statistics, University of Colorado Denver, Denver, CO 80217, USA (e-mail: nathan.graber@ucdenver.edu)
TAO JIANG
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA (e-mail: colliec@miamioh.edu, jiangt@miamioh.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

An r-uniform hypergraph is called an r-graph. A hypergraph is linear if every two edges intersect in at most one vertex. Given a linear r-graph H and a positive integer n, the linear Turán number exL(n,H) is the maximum number of edges in a linear r-graph G that does not contain H as a subgraph. For each ℓ ≥ 3, let Crℓ denote the r-uniform linear cycle of length ℓ, which is an r-graph with edges e1, . . ., eℓ such that, for all i ∈ [ℓ−1], |ei ∩ ei+1|=1, |eℓ ∩ e1|=1 and ei ∩ ej = ∅ for all other pairs {i,j}, i ≠ j. For all r ≥ 3 and ℓ ≥ 3, we show that there exists a positive constant c = cr,ℓ, depending only r and ℓ, such that exL(n,Crℓ) ≤ cn1+1/⌊ℓ/2⌋. This answers a question of Kostochka, Mubayi and Verstraëte [30]. For even ℓ, our result extends the result of Bondy and Simonovits [7] on the Turán numbers of even cycles to linear hypergraphs.

Using our results on linear Turán numbers, we also obtain bounds on the cycle-complete hypergraph Ramsey numbers. We show that there are positive constants a = am,r and b = bm,r, depending only on m and r, such that

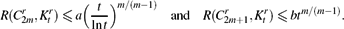\begin{equation} R(C^r_{2m}, K^r_t)\leq a \Bigl(\frac{t}{\ln t}\Bigr)^{{m}/{(m-1)}} \quad\text{and}\quad R(C^r_{2m+1}, K^r_t)\leq b t^{{m}/{(m-1)}}. \end{equation}

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 3 , May 2018 , pp. 358 - 386
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Combin. Theory Ser. A 29 354–360.Google Scholar
[2] Alon, N. (1996) Independence numbers of locally sparse graphs and a Ramsey type problem. Random Struct. Alg. 9 271–278.3.0.CO;2-U>CrossRefGoogle Scholar
[3] Alon, N., Krivelevich, M. and Sudakov, B. (1999) Coloring graphs with sparse neighborhoods. J. Combin. Theory Ser. B 77 73–82.CrossRefGoogle Scholar
[4] Behrend, F. (1946) On sets of integers which contain no three elements in arithmetic progression. Proc. Nat. Acad. Sci. 32 331–332.CrossRefGoogle Scholar
[5] Bohman, T. and Keevash, P. (2010) The early evolution of the H-free process. Invent. Math 181 291–336.Google Scholar
[6] Bohman, T. and Keevash, P. Dynamic concentration of the triangle-free process. arXiv:1302.5963Google Scholar
[7] Bondy, J. A. and Simonovits, M. (1974) Cycles of even length in graphs. J. Combin. Theory Ser. B 16 97–105.CrossRefGoogle Scholar
[8] Brown, W. G., Erdős, P. and Sós, V. (1973) On the existence of triangulated spheres in 3-graphs and related problems. Period. Math. Hungar. 3 221–228.Google Scholar
[9] Bukh, B. and Jiang, Z. (2017) A bound on the number of edges in graphs without an even cycle. Combin. Probab. Comput. 26 1–15.CrossRefGoogle Scholar
[10] Caro, Y. (1979) New results on the independence number. Technical Report, Tel Aviv University.Google Scholar
[11] Caro, Y., Li, Y., Rousseau, C. and Zhang, Y. (2000) Asymptotic bounds for some bipartite graph: Complete graph Ramsey numbers. Discrete Math. 220 51–56.CrossRefGoogle Scholar
[12] Das, S., Lee, C. and Sudakov, B. (2013) Rainbow Turán problem for even cycles. Euro. J. Combin. 34 905–915CrossRefGoogle Scholar
[13] Erdős, P., Faudree, R., Rousseau, C. and Schelp, R. (1978) On cycle-complete graph Ramsey numbers. J. Graph Theory 2 53–64.Google Scholar
[14] Erdős, P. and Rado, R. (1960) Intersection theorems for systems of sets. J. London Math Soc. (2) 35 85–90.Google Scholar
[15] Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc. 52 1087–1091.Google Scholar
[16] Faudree, R. and Simonovits, M. (1983) On a class of degenerate extremal graph problems. Combinatorica 3 83–93.Google Scholar
[17] Fiz Pontiveros, G., Griffiths, S. and Morris, R. The triangle-free process and R(3,k). arXiv:1302.6279Google Scholar
[18] Füredi, Z. (1996) On the number of edges of quadrilateral-free graphs. J. Combin. Theory Ser. B 68 1–6.Google Scholar
[19] Füredi, Z. and Jiang, T. (2014) Hypergraph Turán numbers of linear cycles. J. Combin. Theory Ser. A 123 252–270.Google Scholar
[20] Füredi, Z., Jiang, T. and Seiver, R. (2014) Exact solution of the hypergraph Turán problem for k-uniform linear paths. Combinatorica 34 299–322.Google Scholar
[21] Füredi, Z., Naor, A. and Verstraëte, J. (2006) On the Turán number for the hexagon. Adv. Math. 203 476–496.CrossRefGoogle Scholar
[22] Füredi, Z. and Simonovits, M. (2013) The history of degenerate (bipartite) extremal graph problems. In Erdős Centennial (Lovász, L. et al., eds), Vol. 25 of Bolyai Society Mathematical Studies, Springer, pp. 169–264.Google Scholar
[23] Győri, E. and Lemons, N. (2012) Hypergraphs with no cycle of a given length. Combin. Probab. Comput. 21 193–201.Google Scholar
[24] Győri, E. and Lemons, N. (2012) 3-uniform hypergraphs avoiding a given odd cycle. Combinatorica 32 187–203.Google Scholar
[25] Jiang, T. and Seiver, R. (2012) Turán numbers of subdivided graphs. SIAM J. Discrete Math. 26 1238–1255.CrossRefGoogle Scholar
[26] Li, Y. and Zang, W. (2003) The independence number of graphs with a forbidden cycle and Ramsey numbers. J. Combin. Opt. 7 353–359.CrossRefGoogle Scholar
[27] Keevash, P., Mubayi, D., Sudakov, B. and Verstraëte, J. (2006) Rainbow Turán problems. Combin. Probab. Comput. 16 109–126.CrossRefGoogle Scholar
[28] Kim, J. (1995) The Ramsey number R(3,t) has order of magnitude t 2/logt. Random Struct. Alg. 7 173–207.Google Scholar
[29] Kostochka, A., Mubayi, D. and Verstraëte, J. (2013) Hypergraph Ramsey numbers: Triangles versus cliques. J. Combin. Theory Ser. A 120 1491–1507.Google Scholar
[30] Kostochka, A., Mubayi, D. and Verstraëte, J. Personal communications.Google Scholar
[31] Kostochka, A., Mubayi, D. and Verstraëte, J. (2015) Turán problems and shadows I: Paths and cycles. J. Combin. Theory Ser. A 129 57–79.CrossRefGoogle Scholar
[32] Lazebnik, F. and Verstraëte, J. (2003) On hypergraphs of girth 5. Electron. J. Combin. 10 R25.Google Scholar
[33] Méroueh, A. The Ramsey number of loose cycles versus cliques. arXiv:1504.03668Google Scholar
[34] Molloy, M. and Reed, B. (2002) Graph Colouring and the Probabilistic Method, Vol. 23 of Algorithms and Combinatorics, Springer.Google Scholar
[35] Pikhurko, O. (2012) A note on the Turán function of even cycles. Proc. Amer. Math. Soc. 140 3687–3992.Google Scholar
[36] Roth, K. F. (1951) On a problem of Heilbronn. J. London Math. Soc. 26 198–204.CrossRefGoogle Scholar
[37] Ruzsa, I. (1993) Solving a linear equation in a set of integers I. Acta Arithmetica 65 259–282.Google Scholar
[38] Ruzsa, I. and Szemerédi, E. (1978) Triple systems with no six points carrying three triangles. Colloq. Math. Soc. J. Bolyai 18 939–945.Google Scholar
[39] Sudakov, B. (2002) A note on odd cycle-complete graph Ramsey numbers. Electron. J. Combin. 9 N1.Google Scholar
[40] Verstraëte, J. (2000) On arithmetic progressions of cycle lengths in graphs. Combin. Probab. Comput. 9 369–373.Google Scholar
[41] Wei, V. K. (1981) A lower bound on the stability number of a simple graph. Technical memorandum TM 81-11217-9, Bell Laboratories.Google Scholar