Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T04:00:32.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Longest Increasing Subsequences of Randomly Chosen Multi-Row Arrays

Published online by Cambridge University Press:  02 October 2014

MARCOS KIWI  and
JOSÉ A. SOTO
MARCOS KIWI
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático UMI 2807, Universidad de Chile (e-mail: mk@dim.uchile.cl)
JOSÉ A. SOTO
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático UMI 2807, Universidad de Chile (e-mail: jsoto@dim.uchile.cl)
Get access Rights & Permissions [Opens in a new window]

Abstract

A two-row array of integers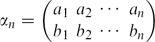

\[ \alpha_{n}= \begin{pmatrix}a_1 & a_2 & \cdots & a_n\\ b_1 & b_2 & \cdots & b_n \end{pmatrix} \]
is said to be in lexicographic order if its columns are in lexicographic order (where character significance decreases from top to bottom, i.e., either ak < ak+1, or bk ≤ bk+1 when ak = ak+1). A length ℓ (strictly) increasing subsequence of αn is a set of indices i1 < i2 < ⋅⋅⋅ < iℓ such that ai1 < ai2 < ⋅⋅⋅ < aiℓ and bi1 < bi2 < ⋅⋅⋅ < biℓ. 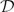We are interested in the statistics of the length of a longest increasing subsequence of αn chosen according to ${\cal D}$n, for different families of distributions 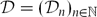${\cal D} = ({\cal D}_{n})_{n\in\NN}$, and when n goes to infinity. This general framework encompasses well-studied problems such as the so-called longest increasing subsequence problem, the longest common subsequence problem, and problems concerning directed bond percolation models, among others. We define several natural families of different distributions and characterize the asymptotic behaviour of the length of a longest increasing subsequence chosen according to them. In particular, we consider generalizations to d-row arrays as well as symmetry-restricted two-row arrays.

Keywords

60C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Special Issue 1: Honouring the Memory of Philippe Flajolet - Part 3 , January 2015 , pp. 254 - 293
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Aldous, D. and Diaconis, P. (1999) Longest increasing subsequences: From patience sorting to the Baik–Deift–Johansson theorem. Bull. Amer. Math. Soc. 36 413–432.CrossRefGoogle Scholar
[2] Arlotto, A., Chen, R. W., Shepp, L. A. and Steele, J. M. (2011) Online selection of alternating subsequences from a random sample. J. Appl. Prob. 48 1114–1132.Google Scholar
[3] Arlotto, A. and Steele, J. M. (2011) Optimal sequential selection of a unimodal subsequence of a random sequence. Combin. Probab. Comput. 20 799–814.CrossRefGoogle Scholar
[4] Arlotto, A. and Steele, J. M. (2014) Optimal sequential selection of an alternating subsequence: A central limit theorem. Adv. Appl. Probab. 46 536–559.CrossRefGoogle Scholar
[5] Babaioff, M., Immorlica, N., Kempe, D. and Kleinberg, R. (2007) A knapsack secretary problem with applications. In Proc. 10th APPROX and 11th RANDOM, pp. 16–28.Google Scholar
[6] Babaioff, M., Immorlica, N. and Kleinberg, R. (2007) Matroids, secretary problems, and online mechanisms. In Proc. 18th SODA, pp. 434–443.Google Scholar
[7] Baik, J., Deift, P. and Johansson, K. (1999) On the distribution of the length of the longest increasing subsequence of random permutations. J. Amer. Math. Soc. 12 1119–1178.Google Scholar
[8] Baik, J. and Rains, E. (2001) Symmetrized random permutations. In Random Matrix Models and their Applications (Bleher, P. M. and Its, A. R., eds), Vol. 40 of Mathematical Sciences Research Institute Publications, Cambridge University Press, pp. 1–19.Google Scholar
[9] Baryshnikov, Y. and Gnedin, A. V. (2000) Sequential selection of an increasing sequence from a multidimensional random sample. Ann. Appl. Probab. 10 258–267.CrossRefGoogle Scholar
[10] Bollobás, B. and Brightwell, B. (1992) The height of a random partial order: Concentration of measure. Ann. Probab. 2 1009–1018.Google Scholar
[11] Bollobás, B. and Winkler, P. (1988) The longest chain among random points in Euclidean space. Proc. Amer. Math. Soc. 103 347–353.Google Scholar
[12] Boshuizen, F. A. and Kertz, R. P. (1999) Smallest-fit selection of random sizes under a sum constraint: Weak convergence and moment comparisons. Adv. Appl. Probab. 31 178–198.Google Scholar
[13] Bruss, F. T. and Delbaen, F. (2001) Optimal rules for the sequential selection of monotone subsequences of maximum expected length. Stoch. Proc. Appl. 96 313–342.Google Scholar
[14] Bruss, F. T. and Delbaen, F. (2004) A central limit theorem for the optimal selection process for monotone subsequences of maximum expected length. Stoch. Proc. Appl. 114 287–311.Google Scholar
[15] Bruss, F. T. and Robertson, J. B. (1991) `Wald's Lemma' for sums of order statistics of i.i.d. random variables. Adv. Appl. Probab. 23 612–623.Google Scholar
[16] Chvátal, V. and Sankoff, D. (1975) Longest common subsequences of two random sequences. J. Appl. Probab. 12 306–315.CrossRefGoogle Scholar
[17] Coffman, E. G., Flatto, L. and Weber, R. R. (1987) Optimal selection of stochastic intervals under a sum constraint. Adv. Appl. Probab. 19 454–473.Google Scholar
[18] Dinitz, M. (2013) Recent advances on the matroid secretary problem. SIGACT News 44 126–142.Google Scholar
[19] Dynkin, E. B. (1963) The optimum choice of the instant for stopping a Markov process. Sov. Math. Doklady 4 627–629.Google Scholar
[20] Gilbert, J. P. and Mosteller, F. (1966) Recognizing the maximum of a sequence. J. Amer. Statist. Assoc. 61 35–73.CrossRefGoogle Scholar
[21] Gnedin, A. V. (2000) A note on sequential selection of permutations. Combin. Probab. Comput. 9 13–17.Google Scholar
[22] Hardy, G., Littlewood, J. E. and Pólya, G. (1952) Inequalities, second edition, Cambridge University Press.Google Scholar
[23] Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs, Wiley.Google Scholar
[24] Kiwi, M. (2006) A concentration bound for the longest increasing subsequence of a randomly chosen involution. Discrete Appl. Math. 154 1816–1823.Google Scholar
[25] Kiwi, M., Loebl, M. and Matoušek, J. (2005) Expected length of the longest common subsequence for large alphabets. Adv. Math. 197 480–498.Google Scholar
[26] Odlyzko, A. and Rains, E. (1998) On longest increasing subsequences in random permutations. Technical report, AT&T Labs.Google Scholar
[27] Rhee, W. and Talagrand, M. (1991) A note on the selection of random variables under a sum constraint. J. Appl. Probab. 28 919–923.Google Scholar
[28] Samuels, S. M. and Steele, J. M. (1981) Optimal sequential selection of a monotone sequence from a random sample. Ann. Appl. Probab. 9 937–947.Google Scholar
[29] Seppäläinen, T. (1997) Increasing sequences of independent points on the planar lattice. Ann. Appl. Probab. 7 886–898.Google Scholar
[30] Stanley, R. (2002) Recent progress in algebraic combinatorics. Bull. Amer. Math. Soc. 40 55–68.Google Scholar