Many Hamiltonian subsets in large graphs with given density

Abstract

A set of vertices in a graph is a Hamiltonian subset if it induces a subgraph containing a Hamiltonian cycle. Kim, Liu, Sharifzadeh, and Staden proved that for large 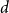$d$, among all graphs with minimum degree 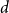$d$, 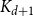$K_{d+1}$ minimises the number of Hamiltonian subsets. We prove a near optimal lower bound that takes also the order and the structure of a graph into account. For many natural graph classes, it provides a much better bound than the extremal one (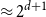$\approx 2^{d+1}$). Among others, our bound implies that an $n$-vertex 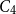$C_4$-free graph with minimum degree 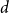$d$ contains at least 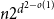$n2^{d^{2-o(1)}}$ Hamiltonian subsets.

1. Introduction

Finding sufficient conditions that guarantee the existence of certain cycles is a well-studied topic in combinatorics. A cycle in a graph is Hamiltonian if it spans the whole vertex set of the graph. Testing whether a graph contains a Hamiltonian cycle is one of Karp’s original NP-complete problems [12]. Dirac’s theorem [3] from $1952$ , arguably the most influential result in this area, asserts that for an $n$ -vertex graph, the minimum degree being at least $\frac n2$ is a tight sufficient condition for containing a Hamiltonian cycle. Since then, various extensions have been studied over the past 70 years, see, e.g., [2, 14, 18, 20, 21] and the survey [19].

In this paper, we study the enumeration problem on Hamiltonian subsets of a graph. A set of vertices $A \subseteq V(G)$ is a Hamiltonian subset if $G[A]$ contains a Hamiltonian cycle. Denote by $h(G)$ the number of Hamiltonian subsets of $G$ . It is natural to ask how $h(G)$ relates to the minimum degree. Intuitively, when the minimum degree is given, larger graphs tend to have more Hamiltonian subsets. In 1981, Komlós conjectured that among all graphs with minimum degree at least $d$ , the complete graph $K_{d+1}$ minimises the number of Hamiltonian subsets. This conjecture was recently confirmed for large $d$ by Kim et al. [13], who also showed that $K_{d+1}$ is the unique minimiser.

While [13] resolves Komlós’s conjecture for large $d$ , it raises multiple related questions. Perhaps the most natural question, considering the $n$ -vertex graph $G^{\star }$ consisting of $\frac{n-1}{d}$ copies of $K_{d+1}$ sharing exactly one common vertex, is whether for any $n$ -vertex graph $G$ with $\delta (G)=d$ , $h(G)=\Omega (n2^d)$ . Also, notice that $G^{\star }$ is basically a disjoint union of $K_{d+1}$ s. If components of a graph are much larger than the unique minimiser $K_{d+1}$ , is it possible to obtain an exponential improvement on $2^d$ ? As we shall see, the relevant parameter is the ‘essential order’ of a graph, captured by the following notion of crux introduced by Haslegrave, Hu, Kim, Liu, Luan, and Wang [8]. Roughly speaking, the crux of a graph is large when the edges are relatively uniformly distributed. We write $d(G)$ for the average degree of $G$ .

Definition (Crux). For a constant $\alpha \in (0,1)$ , a subgraph $H\subseteq G$ is an $\alpha$ -crux if $d(H)\ge \alpha \cdot d(G)$ . The $\alpha$ -crux function, $c_\alpha (G)$ , of $G$ is defined as the order of a minimum $\alpha$ -crux in $G$ , that is,

\begin{equation*} c_\alpha (G)=\min \{ \lvert H\rvert \colon H \subseteq G \text { and } d(H) \ge \alpha \cdot d(G) \}.\end{equation*}

Here are some common graph classes for which $c_{\alpha }(G)\gg d(G)$ : $(i)$ $K_{s,t}$ -free graphs $G$ with $t \ge s \ge 2$ , satisfy $c_\alpha (G)=\Omega \big (d(G)^{s/(s-1)}\big )$ (as a corollary of $\mathrm{ex}(n, K_{s,t})=O\left (n^{2-1/s}\right )$ ); $(ii)$ a $\frac{d}{r}$ -blow-up $G$ of a $d$ -vertex $r$ -regular expander graph for a sufficiently large constant $r$ satisfies $c_\alpha (G)=\Omega (d^2)$ and $d(G)=d$ ; and $(iii)$ there are well-studied graphs whose crux size is exponentially larger than its average degree, e.g. using isoperimetry inequalities, one can show that the $d$ -dimension hypercube $Q^d$ satisfies $c_\alpha (Q^d)\ge 2^{\alpha d}$ . For more details, we refer the readers to [8].

Our main result reads as follows.

Theorem 1.1. There exist constants $B$ and $d_0$ such that the following is true. Let $G$ be an $n$ -vertex graph with average degree $d\ge d_0$ , $t=c_{\frac{1}{5}}(G)$ and $\beta =(6000\log 3)^{-16}$ , then

\begin{equation*}h(G)\ge \frac {1}{B}n2^{\beta t/\log ^{16}t}.\end{equation*}

Our bound is optimal up to the constant factor $B$ and the polylog factor in the exponent (consider again $G^{\star }$ ). Also $\frac 15$ in the crux function can be replaced by any constant strictly smaller than $\frac 12.$ It improves on the extremal bound $h(K_{d+1})\approx 2^{d+1}$ in two aspects as suggested above, i.e. having a factor linear in the order $n$ and an exponential (in $d$ ) improvement for graphs whose crux size is much larger than their average degree. For example, for a $C_4$ -free graph $G$ , using the lower bound on crux in $(i)$ above, we get $h(G)\ge n2^{d^{2-o(1)}}$ .

It is worth mentioning that Theorem 1.1 is another manifestation of the replacing average degree by crux paradigm proposed in Haslegrave et al. [8]. It suggests that one might be able to replace the appearance of $d(G)$ in results on sparse graph embeddings with the crux size $c_\alpha (G)$ instead. The essential reason that we can replace the average degree by crux in the exponent for $h(G)$ is that large crux implies existence of certain large expander subgraph which supplies many Hamiltonian subsets. We refer the readers to [8, 11] for more results illustrating this paradigm.

As in [13], our proof also utilises the notion of sublinear expanders. The theory of sublinear expanders, first introduced by Komlós and Szemerédi [15, 16] in the 1990s, has played a pivotal role in many recent resolutions of old conjectures, see, e.g., [4, 5, 7–10, 13, 22–24]. However, after passing to a sublinear expander subgraph, we take a completely different approach than [13] to construct Hamiltonian subsets. Indeed, in [13], they used a set of $\Theta (d)$ vertices that are pairwise far apart to produce exponential in $d$ many Hamiltonian subsets. For us, to have the additional factor linear in the order $n$ , we instead find a positive fraction of vertices, each contained in many distinct Hamiltonian subsets. To this end, we repeatedly apply the following result, which could be of independent interest; it guarantees one such ‘heavy’ vertex, in dense subgraphs of the host graph.

Theorem 1.2. Let $0\lt \alpha \lt \frac{1}{2}$ , $G$ be a graph with sufficiently large average degree $d$ and $t=c_{\alpha }(G)$ . Then there exists a vertex lying in at least $2^{\beta t/\log ^{16} t}$ distinct Hamiltonian subsets, where $\beta =(6000\log 3)^{-16}$ .

We find such ‘heavy’ vertices via embedding a large wheel-like structure (see Definition 2.6), inspired by the adjuster structure in Liu-Montgomery [23], in sublinear expander subgraphs of $G$ . To construct such a large wheel, we perform an exploration algorithm similar to depth-first search (DFS) on a collection of suitable cycles. In particular, the cycles we use all have polylogarithmic length ( $(\log n)^{\Theta (1)}$ ), which result in the polylog factor loss in the exponents of both Theorems 1.1 and 1.2.

It would be interesting to know whether the polylog factor in the exponent in Theorem 1.1 is necessary or just the artefact of our method. Note that expanders with constant expansion (i.e. positive Cheeger constant) could have girth polylogarithmic in $n$ , so our approach cannot be applied to delete the polylog factor even if we have better expansion property. On the other hand, we observe that the polylog factor is not necessary for $(n,d,\lambda )$ -graphs. The $(n,d,\lambda )$ -graphs are $d$ -regular graphs on $n$ vertices with second largest eigenvalue in absolute value $\lambda$ . It is not hard to see that the crux size of an $(n,d,\lambda )$ -graph is linear in $n$ when $\lambda$ is bounded away from $d$ , see Proposition 2.10.

Proposition 1.3. Let $0\lt \beta \lt 1$ and $G$ be an $(n,d,\lambda )$ -graph. If $\frac{d}{|\lambda |} \ge \frac{1}{\beta ^2}$ , then $ h(G) \ge \binom{n}{\frac{1}{2}n}/ \binom{(\frac{1}{2}+ 3 \beta )n}{3\beta n}$ . Specifically, if $\beta \lt 1/6$ , then $h(G) \ge 2^{(\frac{1}{2}-3\beta )n}$ .

Organisation. The rest of the paper is organised as follows. In Section 2, we list some preliminaries needed for the proof. In Section 3, we prove Theorem 1.2. In Section 4, we prove the main result, Theorem 1.1. Proposition 1.3 is proved in Section 5 and concluding remarks in Section 6.

2. Notations and preliminary properties

A ball of radius $r$ (around a vertex $v$ ), denoted by $B_G^{r}(v)=\{u \in V \colon 0 \le d(u,v) \le r\}$ , in a graph $G$ is the set of all vertices which are at distance no more than $r$ from $v$ . Here we write $B^r(v)$ if the underlying graph we consider is clear. For a vertex set $X,$ the ball around $X$ of radius $r$ is similarly defined as the set of all vertices at distances at most $r$ from (some vertex in) $X$ , that is, $B^{r}(X)=\bigcup _{v \in X}B^{r}(v)$ . We write $G-X=G[V(G)\setminus X]$ for the subgraph induced on $V(G)\setminus X$ . Throughout the paper, $\log$ denotes the natural logarithm.

2.1 Sublinear expanders

For $\varepsilon _1 \gt 0$ and $k\gt 0$ , let $\varepsilon (x,\varepsilon _1,k)$ be the function

(1) \begin{align} \varepsilon (x,\varepsilon _1,k) = \left \{ \begin{array}{lr} 0 &\quad \text{if}\ x\lt k/5, \\ \varepsilon _1/\log ^2(15x/k) &\quad \text{if}\ x\ge k/5, \end{array} \right . \end{align}

where, when it is clear from context, we will write $\varepsilon (x,\varepsilon _1,k)$ as $\varepsilon (x).$

Definition 2.1 (Sublinear expander). A graph $G$ is an $(\varepsilon _1, k)$ -expander if for any subset $X \subseteq V(G)$ of size $k/2 \le |X| \le |V(G)|/2$ , we have $|N_G(X)| \ge \varepsilon (|X|)\cdot |X|$ .

A classical result of Komlós and Szemerédi states that any graph $G$ contains a sublinear expander subgraph retaining almost the same average degree. A priori, this subgraph can have much smaller order than $G$ , but by definition, this sublinear expander subgraph is at least as large as the crux (say $c_{\frac{1}{2}}(G)$ ). We remark that this was in fact one of the motivations for the notion of crux.

Lemma 2.2 (Lemma 2.2, [8]). Let $C\gt 30,\varepsilon _1\le 1/(10C),k \gt 0$ and $d \gt 0$ . Then every graph $G$ with $d(G) = d$ has a subgraph $H$ such that $H$ is an $(\varepsilon _1,k)$ -expander, $d(H) \ge (1-\delta )d$ and $\delta (H) \ge d(H)/2$ , where $\delta :\!= \frac{C \varepsilon _1}{\log 3}$ .

The following lemma is a slightly modified version of Theorem 3.12 in [23]. It finds linear-size balls robustly in sublinear expanders. By size of a ball, we mean the number of vertices in the ball.

Lemma 2.3. For any $0\lt \varepsilon _1\lt 1$ the following holds for each $n\geq 60$ . Suppose that $G$ is an $n$ -vertex $(\varepsilon _1,15)$ -expander. For any set $W\subseteq V(G)$ with $|W|\leq \varepsilon _1 \frac{n}{20\log ^{2}n}$ , there is a ball $B\subseteq G-W$ with size at least $n/10$ and radius at most $\frac{20}{\varepsilon _1}\log ^3n$ .

Lemma 2.4 (Proposition 3.10, [23]). For every $m'\le m$ the following is true. Every ball $B^r(v)$ of radius $r$ with size $m$ contains a connected subgraph of radius at most $r$ with centre $v$ and size $m'.$

A key property of expanders is the following short diameter property.

Lemma 2.5 (Corollary 2.3, [16]). Let $\varepsilon _1\gt 0$ , $H$ be an $n$ -vertex $(\varepsilon _1,15)$ -expander and $X,X',W\subseteq V(H)$ . If $|X|,|X'|\ge x\ge 8$ and $|W|\le \frac{1}{4}\varepsilon (x)x$ , then there is a path in $H-W$ from $X$ to $X'$ of length at most $\frac{2}{\varepsilon _1}\log ^3n$ .

2.2 Large wheels in expanders

To find vertices in many Hamiltonian subsets, we use the following structures.

Definition 2.6 (Chain/wheel). An $\ell$ -chain/ $\ell$ -wheel is the graph obtained from a path/cycle by replacing $\ell$ edges in the path/cycle with $\ell$ cycles, which are disjoint up to possible common end-vertices of the initial edges.

Examples of a chain and a wheel are depicted in Fig. 1. It is easy to see that an $\ell$ -wheel has at least $2^\ell$ different Hamiltonian subsets, since for each of the $\ell$ cycles there are two choices for a path between the end-vertices of the initial edge it replaced.

Figure 1. A $3$ -chain and a $4$ -wheel.

The following lemma finds an almost linear-size wheel in a sublinear expander, from which we can quickly derive Theorem 1.2. The proof of Lemma 2.7 will be given in Section 3.

Lemma 2.7. Let $0\lt \varepsilon _1 \lt 1$ and $H$ be an $(\varepsilon _1, 15)$ -expander of order $n$ , where $n$ is sufficiently large. Then there exists an $\ell$ -wheel in $H$ with $\ell \ge \left (\frac{\varepsilon _1}{20} \right )^{16} (2n/\log ^{16} n)$ .

2.3 Crux function

We also need some control on the crux function and the expander mixing lemma.

Lemma 2.8 (Expander mixing lemma [1]). For any $(n,d,\lambda )$ -graph $G$ and two vertex subsets $X$ and $Y$ , we have $\bigg |e(X,Y) -\frac{d}{n}|X||Y|\bigg |\le \lambda \sqrt{|X||Y|\left (1-\frac{|X|}{n}\right )\left (1-\frac{|Y|}{n}\right )}$ .

Proposition 2.9. For every graph $G$ with average degree $d$ and every $0 \lt \alpha \lt \alpha ' \lt 1$ , we have

\begin{equation*}c_{\alpha }(G) \le \left \lceil \frac {\alpha }{\alpha '}(c_{\alpha '}(G)-1)+1\right \rceil .\end{equation*}

In particular, for a graph $G$ , for every $0\lt \alpha \lt 1$ , $c_{\alpha }(G) \le \left \lceil \alpha (|G|-1)+1\right \rceil .$

Proof. Let $G'$ be the graph on $n\,{:\!=}\,c_{\alpha '}(G)$ vertices for which the average degree is at least $\alpha ' d.$ By definition of the crux, it suffices to prove that there exists a subgraph $H$ of $G'$ with at most $k:\!=\left \lceil \frac{\alpha }{\alpha '}(n-1)+1\right \rceil$ vertices for which the average degree is at least $\alpha d.$ For this, consider a uniform random $k$ -vertex induced subgraph $H$ of $G'$ . The probability that a particular edge $uv$ of $G$ belongs to such a subgraph equals $\frac{\binom{n-2}{k-2}}{\binom{n}{k}}=\frac{\binom k2}{\binom{n}{2}}.$ The expected size of $H$ equals $\mathbb{E}(E(H)) =e(G') \frac{\binom k2}{\binom{n}{2}}.$ Hence the expected average degree equals

\begin{align*} \mathbb{E}(d(H)) = \frac{2\mathbb{E}(E(H))}{k} \ge \frac{\alpha ' d n }{k}\frac{\binom k2}{\binom{n}{2}} =\frac{ \alpha 'd(k-1)}{n-1}\ge \alpha d. \end{align*}

This implies that there exists at least one subgraph $H \subset G$ with order $k$ and $d(H) \ge \alpha d$ .

We remark (even while not needed in the remaining of the exposition) that Proposition 2.9 is sharp for $G=K_{d+1},$ since $H=K_{\alpha d+1}$ is the minimum subgraph of $G$ with average degree at least $\alpha d.$ More generally, it is asymptotically sharp for $(n,d,\lambda )$ -graphs.

Proposition 2.10. Let $0 \lt \alpha \lt 1$ . Given $\varepsilon \gt 0$ , if $\frac{\lambda }{d}\lt \varepsilon \alpha$ , then for every $(n,d,\lambda )$ -graph $G=(V,E)$

\begin{equation*}c_{\alpha }(G) \gt (1-\varepsilon )\alpha n.\end{equation*}

Proof. Assume there exists a set $S$ such that $d(G[S]) \ge \alpha d$ and $\lvert S\rvert \lt (1-\varepsilon )\alpha n.$ Then

\begin{equation*}\lvert e(S, V \backslash S)\rvert \le (1-\alpha ) d \lvert S\rvert = (1-\alpha +\alpha \varepsilon ) d \lvert S\rvert - \alpha \varepsilon d \lvert S\rvert \lt d \lvert S\rvert \frac {\lvert V \backslash S\rvert }{\lvert V\rvert } - \lambda \lvert S\rvert .\end{equation*}

This is a contradiction with the expander mixing lemma.

2.4 Depth-first search

One of the main ideas in this paper is an algorithm that is similar to DFS, see step 2 in Section 3. DFS is a graph exploration algorithm that visits all the vertices of an input graph. Here we summarise the DFS algorithm for a graph $G=(V,E)$ . Let $S$ be a stack (initially the empty set), consisting of vertices in $V$ . Let $U$ be a set (initially $V$ ) of unexplored vertices in $V$ , and let $X$ be a set (initially the empty set) of explored vertices in $V$ . In every step, if $S$ is empty and $|U|\gt 0$ , then we take an arbitrary element from $U$ and put it into $S$ . If the top vertex of $S$ has a neighbour in $U$ , move such a neighbour from $U$ to put it on top of $S$ . If the top vertex of $S$ has no neighbour in $U$ , move the top vertex of $S$ to $X$ . Stop when $X=V$ .

The following properties hold throughout the process.

1. 1. The stack $S$ forms a path in $G$ .

2. 2. There is no edge of $G$ between $U$ and $X$ .

3. Finding many Hamiltonian subsets with a common vertex

In this section, we will prove Lemma 2.7 in three steps and derive Theorem 1.2 from it. Throughout the proof, we let

\begin{equation*}p= \frac {20}{\varepsilon _1} \log n,\quad t=\frac {n}{p^{10}},\quad r = \frac {2}{\varepsilon _1}\log ^3 n.\end{equation*}

We also assume that $\varepsilon _1\lt 1$ and $n$ is sufficiently large, such that the inequalities used in the proof are true.

First, we prove that expanders contain many disjoint cycles of appropriate length.

Step 1: finding many disjoint cycles

Proposition 3.1. Let $H$ be an $(\varepsilon _1,15)$ -expander of order $n$ . Then $H$ contains at least $t$ disjoint cycles, all of whose lengths are between $p^5$ and $p^6.$

Proof. Let $\mathcal{C}$ be a maximal collection of disjoint cycles of length between $p^5$ and $p^6$ . Suppose to the contrary that $|\mathcal{C}|\lt t$ . For ease of the reader, Figure 2 gives a depiction of the following steps in the remaining of the proofs. Let $W$ be the set of vertices contained in these cycles. Note that $\lvert W\rvert \lt tp^6=\frac{n}{p^4}.$ By applying Lemmas 2.3 and 2.4 twice, we can find two disjoint sets $D$ and $D'$ with diameter at most $p^3$ and size $\frac{n}{p^2}$ which avoid $W$ . For this, it is sufficient to note that $\frac{n}{p^2}+\frac{n}{p^4}\lt \varepsilon _1 \frac{n}{20 \log ^2 n}$ and thus once $D$ is constructed, one can find a large ball avoiding $W \cup D$ (by Lemma 2.3) and take a set $D'$ of the right size (by Lemma 2.4).

Figure 2. The sets $D,D',X,W$ and path $P$ and extension in the final step in Proposition 3.1.

Let $x=\frac n{p^2}.$ Note that $\varepsilon (x)/4=\frac{\varepsilon _1}{4\log ^2 x} \ge \frac{\varepsilon _1}{4\log ^2 n}\gt \frac{1}{p^2}$ and thus $\lvert W\rvert \lt \frac{n}{p^4}=\frac{x}{p^2}\lt x \varepsilon (x)/4.$ Hence by Lemma 2.5 we can find a path of length at most $p^3$ connecting $D$ and $D'$ while avoiding $W$ .

Now iteratively, we can build longer paths between two sets of size $\frac{n}{p^2}=tp^8$ and diameter at most $p^3$ until the length is between $p^5$ and $p^5+2p^3$ , in such a way that the length increases in each step by at least one and at most $2p^3$ . Let $D$ and $D'$ be the two current sets, with a path from $v\in D$ to $v'\in D'$ , say $P$ . Let $X$ be a set of size $tp^8$ and diameter at most $p^3$ which avoids $D,D'$ , $W$ , and $V(P)$ . The latter is possible by Lemmas 2.3 and 2.4 as $2\frac{n}{p^2}+\frac{n}{p^4} + p^5\lt \varepsilon _1 \frac{n}{20 \log ^2 n}.$ Take a path of length at most $p^3$ between $X$ and $D \cup D'$ avoiding $W$ and $P$ , which is again possible by Lemma 2.5. Without loss of generality, this path is between $x \in X$ and $ d \in D'$ . As such, we can consider $X$ and $D$ as the new sets and the union of the paths between $x$ and $d$ , $d$ and $v'$ , and $v'$ and $v$ as the new path $P'$ . Then $|P|\lt |P'| \le |P| +p^3 +p^3$ .

By iterating this, we reach a path $P_1$ of length between $p^5$ and $p^5+2p^3$ between the two sets $D$ and $D'$ . Applying Lemma 2.5 a final time, gives a path $P_2$ , avoiding $W$ and $P_1$ , between $D$ and $D'$ of length at most $p^3.$ The union of $P_1, P_2$ and $2$ connecting paths in $D$ and $D'$ gives a cycle of length between $p^5$ and $p^5+6p^3\lt p^6$ . This cycle is disjoint from those in $\mathcal{C}$ , contradicting the maximality of $\mathcal{C}$ .

Step 2: finding a long chain

Having found many disjoint cycles in Step 1, we now prove that we can connect some of them in a chain. Here we use an algorithm, similar to DFS, where we explore the set of cycles (instead of set of vertices).

Proposition 3.2. Let $0\lt \varepsilon _1 \lt 1$ and $H$ be an $(\varepsilon _1,15)$ -expander of order $n$ . Let $p= \frac{20}{\varepsilon _1} \log n, t=\frac{n}{p^{10}}$ and $r = \frac{2}{\varepsilon _1}\log ^3 n$ . If $H$ contains at least $t$ disjoint cycles, all of whose lengths are between $p^5$ and $p^6$ , then there exists an $\ell$ -chain with $ \ell \ge t/ p^3$ and each path between two consecutive cycles on the chain has length at most $r=\frac{2}{\varepsilon _1} \log ^3 n$ .

Proof. Let $\mathcal{C}$ be a set consisting of $t$ disjoint cycles, all of whose lengths are between $p^5$ and $p^6$ . To find the desired chain, we perform a process similar to DFS on $\mathcal{C}$ .

During the process, We keep track of the following four sets:

• • a stack $S$ (initially the empty set), consisting of cycles (which are ordered) in $\mathcal{C}$ ,

• • a set $U$ (initially $\mathcal{C}$ ) of unexplored cycles in $\mathcal{C}$ ,

• • a set $X$ (initially the empty set) of explored cycles in $\mathcal{C}$ ,

• • a set $\mathcal{P}$ (initially the empty set) of pairwise (vertex) disjoint paths.

In every step, we do one of the following replacements.

• • If $S$ is empty and $|U|\gt 0$ , then take an arbitrary element from $U$ and put it to the top of $S$ .

• • If $S$ is not empty and $|U|\gt 0$ and

  1. – if there exists a path $P$ of length at most $r$ , all of whose internal vertices do not belong to (a cycle of) $\mathcal{C}$ nor (a path in) $\mathcal{P}$ , which connects the top element in $S$ and an arbitrary cycle $C$ in $U$ , then we remove the cycle $C$ from $U$ and push it onto the top of $S$ , and push the path $P$ into $\mathcal{P}$ ,

  2. – if no such path $P$ exists, then take the top element from $S$ and put it into $X$ .

• • If $|U|=0$ , then stop.

Throughout the process, observe that

1. 1. at any step of the process, there exists an $|S|$ -chain which connects all cycles in $S$ and each path between two consecutive cycles has length at most $r$ ;

2. 2. there does not exist a path $P$ , whose internal vertices are not in $\mathcal{C}$ and $\mathcal{P}$ , with length at most $r$ , which connects (a cycle in) $X$ and (a cycle in) $U$ ; and

3. 3. $|\mathcal{P}| \le |\mathcal{C}| - |U|$ .

We run this process until the point that $|U| = \frac t3$ . Suppose to the contrary that $|S|\lt t/p^3$ . Then $|X|=t-|U|-|S| \ge t/3$ and $|\mathcal{P}|\le 2t/3$ . Observe also that

\begin{align*} &\sum _{C\in X} |C|, \sum _{C\in U} |C| \ge t/3 \cdot p^5,\\ &\sum _{P\in \mathcal{P}} |P| \le 2t/3 \cdot r = \frac{4t}{3\varepsilon _1} \log ^3 n \le \frac{\varepsilon _1tp^5}{24 \log ^2 n} \le \varepsilon (tp^5/3)tp^5/24 \quad \mbox{and}\\ &\sum _{ C \in S } |C| \le tp^3 \le \varepsilon (tp^5/3)tp^5/24. \end{align*}

Let $W =\bigcup _{P\in \mathcal{P} } V(P) \cup \bigcup _{C\in S} V(C)$ , then $ |W| \le \varepsilon (tp^5/3)tp^5/12$ . By Lemma 2.5, there exists a path avoiding vertices in $W$ with length at most $r$ between $X$ and $U$ , a contradiction. Hence $|S|\ge t/p^3$ and Observation 1 above implies the result.

Step 3: finding a long wheel

Finally, we prove that one can add a path between two cycles (near the ends) of the chain, to find a wheel. To do so, we need to have sufficiently many cycles at the ends to be able to connect them with Lemma 2.5.

Proposition 3.3. Let $0\lt \varepsilon _1 \lt 1$ and $H$ be an $(\varepsilon _1,15)$ -expander of order $n$ . Let $p= \frac{20}{\varepsilon _1} \log n, t=\frac{n}{p^{10}}$ , and $r = \frac{2}{\varepsilon _1}\log ^3 n$ . If $H$ contains an $m$ -chain with $m= t/p^3$ such that each cycle has length between $p^5$ and $p^6$ and each path between two consecutive cycles has length at most $r$ . Then $H$ contains an $\ell$ -wheel with $\ell \ge 2t/p^6$ .

Proof. Let $S= C_1P_1C_2\ldots P_{m-1}C_m$ be the $m$ -chain with $|P_i|\le r$ . We shall expand and connect two ends of this chain while avoiding a small middle segment to obtain a desired wheel. More precisely, let

\begin{align*} &X_1= \bigcup _{i=1}^{m/2-m/p^3} V(C_i), \ W = \left ( \bigcup _{i=m/2-m/p^3+1}^{m/2+m/p^3} V(C_i) \right ) \cup \bigcup _{i=1}^{m} V(P_i), \ X_2= \bigcup _{i=m/2+m/p^3+1}^{m} V(C_i). \end{align*}

It is easy to check $|X_i| \ge m/3\cdot p^5$ for $i=1,2$ , and $|W| \le 2m/p^3 \cdot p^6 + m \cdot p^3 \le \varepsilon ( mp^5/3)mp^5/12$ , since $r\lt p^3$ and $\log (mp^5/3)\lt \log n$ . By Lemma 2.5, there exists a path $P$ avoiding $W$ between $X_1$ and $X_2$ , say between $C_i$ and $C_j$ for some $1\le i\le m/2-m/p^3$ and $m/2+m/p^3+1\le j\le m$ . Then the union of $P$ and $C_iP_iC_{i+1}\ldots P_{j-1}C_j$ forms an $\ell$ -wheel with $ \ell \ge 2m/p^3 = 2t/p^6$ , where possibly $C_i$ and/or $C_j$ are deleted when $P$ has an end-vertex equal to $C_i \cap P_i$ and/or $C_{j} \cap P_{j-1}$ .

So we can find an $\ell$ -wheel with $ \ell \ge 2n/p^{16} =(\frac{\varepsilon _1}{20})^{16} (2n/\log ^{16} n)$ in $H$ . Lemma 2.7 now follows immediately from Propositions 3.1, 3.2, and 3.3.

Proof of Theorem 1.2. Take $C=30\log 3$ and $\varepsilon _1 = 1/(10C)$ . By Lemma 2.2, there exists an $(\varepsilon _1, 15)$ -expander $H$ in $G$ such that $d(H) \ge (1-\delta ) d\gt \alpha d$ . Thus, by the definition of crux, we have $n :\!=\lvert H\rvert \ge t=c_{\alpha }(G)$ . Then by Lemma 2.7 there exists an $\ell$ -wheel in $H$ (and thus also in $G$ ) with $\ell \ge \left (\frac{\varepsilon _1}{20} \right )^{16} (2n/\log ^{16} n) \ge 2\beta t/\log ^{16}t$ . Since an $\ell$ -wheel contains $2^\ell$ different cycles and any vertex in an $\ell$ -wheel is contained in at least $2^{\ell -1}$ different cycles, we conclude.

4. Proof of the main theorem

In this section, we prove Theorem 1.1. We shall perform three counting strategies and show that at least one results in the desired lower bound for the number of Hamiltonian subsets. We start with a smallest counterexample $G$ and in the first two strategies, we shall find many vertices belonging to many (different) Hamiltonian subsets. If those strategies fail to produce enough Hamiltonian subsets, then $G$ must contain a dense subgraph with sufficiently many Hamiltonian subsets.

Proof of Theorem 1.1. Recall that $t=c_\alpha (G)$ , $\alpha =1/5$ , $\varepsilon _1=\frac{1}{300\log 3}$ and $\beta =\left ( \frac{\varepsilon _1}{20} \right )^{16}$ . Choose $d_0$ such that $\beta x\gt \log ^{16} x$ whenever $x \ge \alpha d_0$ and Theorem 1.2 is true whenever $d \ge d_0$ . Then choose the constant $B$ such that $\beta bt/\log ^{16}(bt)\gt \beta t/\log ^{16}t + \log _2(5b)$ whenever $b \ge \frac{B}{5}$ and $t \ge \alpha d_0.$

Let $G$ be a graph with average degree $d\ge d_0$ with minimum order $n$ among all graphs for which the theorem is not true. That is, $h(G) \lt \frac{n}{B} 2^{\beta t/\log ^{16}t}$ , and for any proper subgraph of $G$ , say $G'$ , if the average degree of $G'$ is at least $d_0$ , then $h(G')\ge \frac{|V(G')|}{B} 2^{\beta t'/\log ^{16}t'}$ , where $t'=c_\alpha (G')$ .

We now consider three strategies.

Strategy 1:

We will choose a set of vertices $S$ in which every vertex belongs to at least $2^{\beta t/\log ^{16} t}$ different Hamiltonian subsets of $G$ . Let $S$ be a set of vertices, which is initially the empty set. As long as $G - S$ has average degree at least $\frac d4,$ by Lemma 2.2 there exists an $(\varepsilon _1,15)$ -expander $H \subset G- S$ with minimum degree at least $\frac d5$ . So $H$ has order at least $c_{\alpha }(G).$ By Theorem 1.2, there is a vertex $s$ in $H$ belonging to at least $2^{\beta t/\log ^{16} t}$ distinct Hamiltonian subsets. Now add $s$ to $S$ . If at the end, $S$ contains at least $\frac{n}{B}$ vertices, we would reach a contradiction with the choice of $G$ , being a graph with less than $\frac{n}{B} 2^{\beta t/\log ^{16} t}$ Hamiltonian subsets.

We may then assume that $|S|\lt \frac{n}{B}$ . Note also that $G-S$ , having average degree less than $\frac d4$ , contains less than $\frac{d(n-\lvert S\rvert )}{8}\lt \frac{m}{4}$ edges, where $m=e(G)$ .

Strategy 2:

We restart the search for Hamiltonian subsets in the bipartite graph $G[S, V \backslash S]$ , where $S$ is the set constructed while executing Strategy $1.$ As long as the bipartite graph $G[S, V \backslash S]$ contains at least $\frac{m}{4}$ edges, and hence has average degree at least $\frac d4,$ by Lemma 2.2 there exists an $(\varepsilon _1,15)$ -expander $H \subset G[S, V \backslash S]$ with minimum degree at least $\frac d5$ and hence $H$ has order at least $c_{\alpha }(G).$ Take a vertex $s \in V \backslash S$ , then by Theorem 1.2 there are at least $2^{\beta t/\log ^{16}t}$ Hamiltonian subsets containing $s.$ Now add $s$ to $S$ . If $G[S, V \backslash S]$ contains at least $\frac{m}{4}$ edges, repeat this process.

We claim that we do not count the same Hamiltonian subset twice. For two different vertices $s_1$ and $s_2$ which we added to $S$ in Strategy 2, let $S_i$ be the set $S$ before we move $s_i$ , for $i=1,2$ , then $s_i \notin S_i$ . Without loss of generality, assume that we added $s_1$ to $S$ before $s_2$ , i.e. $S_1\subset S_2$ , then $s_1\in S_2$ and $s_2 \notin S_1$ . Let $H$ be a Hamiltonian subset containing both $s_1$ and $s_2$ . Since $s_1 \notin S_1, s_1 \in S_2$ and $s_1 \in H$ , we have $|H \cap S_1|\lt |H \cap S_2|$ . On the other hand, if $H$ was counted on both times, we would have $|H \cap S_1| = |H \cap S_2| = |H|/2$ (as $G[S_i,V\setminus S_i]$ is bipartite and $|H|$ is even), a contradiction. If we can repeat this at least $\frac{n}{B}$ times, we have found the desired number of Hamiltonian subsets again, which would be the desired contradiction.

Strategy 3:

After performing the two previous strategies, we ended up with a set $S$ such that $G- S$ and $G[S, V \backslash S]$ both contain less than $\frac{m}{4}$ edges, so $G[S]$ contains at least $\frac{m}{2}$ edges. Also we know that $\lvert S\rvert =\frac{1}{b} n \le 2\frac{n}{B},$ for some $b \ge \frac B2.$ Hence the average degree of $G[S]$ is $\gamma d$ for some $\gamma \ge \frac b2.$ By Proposition 2.9, this implies that $ \left \lceil \frac{1}{\gamma }( c_\alpha (G[S])-1) +1\right \rceil \ge c_{\alpha/\gamma }(G[S]) \ge c_{\alpha }(G)$ and thus $\gamma (c_\alpha (G)-2)\lt c_\alpha (G[S]) = b' c_{\alpha }(G)=b't$ for some $b' \ge \frac{4\gamma }{5} \ge \frac{2b}{5} \ge \frac B5$ . Since $G$ is a minimal counterexample, $G[S]$ satisfies

\begin{align*} h(G[S]) &\ge \frac{n/b}{B} 2^{\beta b't/\log ^{16}(b't)} \ge 5b' \frac{n/b}{B} 2^{\beta t/\log ^{16}t} \ge \frac{n}{B} 2^{\beta t/\log ^{16}t}. \end{align*}

Since $h(G) \ge h(G[S])$ , we derive the final contradiction.

5. Proof of Proposition 1.3

We shall prove a similar bound for a larger class of $\beta$ -graphs (see [6]). For $0\lt \beta \lt 1$ , an $n$ -vertex graph $G$ is a $\beta$ -graph if every pair of disjoint vertex sets $A,B\subseteq V(G)$ of size $|A|,|B|\gt \beta n$ are connected by an edge. Note that by the expander mixing lemma, Lemma 2.8, an $(n,d,\lambda )$ -graph with $\frac{d}{|\lambda |} \ge \frac{1}{\beta ^2}$ is a $\beta$ -graph. Hence, Proposition 1.3 follows from the following result.

Proposition 5.1. Let $G$ be an $n$ -vertex $\beta$ -graph, then $ h(G) \ge \binom{n}{\frac{1}{2}n}/ \binom{(\frac{1}{2}+ 3 \beta )n}{3\beta n}$ . Specifically, if $\beta \lt 1/6$ , then $h(G) \ge 2^{(\frac{1}{2}-3\beta )n}$ .

We first show that large subgraphs of a $\beta$ -graph contain almost spanning cycles.

Lemma 5.2. Let $G$ be an $n$ -vertex $\beta$ -graph and $0\lt c\lt 1$ . Then for every subset $S$ with $cn$ vertices, $G[S]$ contains a cycle of length at least $(c-3\beta )n.$

To prove this lemma, we need the following result.

Lemma 5.3 ([17], Theorem 1). Let $k\gt 0,t\ge 2$ be integers. Let $G$ be a graph on more than $k$ vertices, satisfying that $|N_G(W)| \ge t$ , for every $W \subseteq V(G)$ with $k/2 \le |W| \le k$ . Then $G$ contains a cycle of length at least $t+1$ .

Proof of Lemma 5.2. By definition of a $\beta$ -graph, for any vertex set $U$ , if $\lvert U\rvert \ge \beta n$ , then we have $\lvert N_G(U)\rvert \gt n-|U| -\beta n$ , for otherwise $U$ and $V \backslash (U\cup N(U))$ would be two sets of size at least $\beta n$ without an edge in between, a contradiction. Let $W$ be any subset of $S$ of size $\beta n \le \lvert W\rvert \le 2\beta n$ . Then $\lvert N_{G[S]}(W)\rvert \ge \lvert N_G(W)\rvert - (n-\lvert S\rvert ) \ge n- 3 \beta n-(1-c)n=(c-3\beta )n$ . Now the result follows from Lemma 5.3.

Proof of Proposition 5.1. By Lemma 5.2, for any vertex set $S$ of size $\frac{1}{2}n$ , we can find a cycle of length at least $(\frac{1}{2} -3\beta )n$ . For any such cycle $C_\ell$ , with $(\frac{1}{2} -3\beta )n \le \ell \le n/2$ , it is contained in at most $\binom{n-\ell }{n/2-\ell } \le \binom{\left (\frac{1}{2}+ 3 \beta \right )n}{3\beta n}$ different subsets of size $n/2$ . So we can find at least $\binom{n}{\frac{1}{2}n}/ \binom{\left (\frac{1}{2}+ 3 \beta \right )n}{3\beta n}$ Hamiltonian sets.

If $\beta \lt 1/6$ , we have

\begin{equation*} \binom {n}{\frac {1}{2}n}/ \binom {\left (\frac {1}{2}+ 3 \beta \right )n}{3\beta n} =\frac {n\cdot \left (n-1\right ) \cdot \ldots \cdot \left (n-\left (1/2 -3\beta \right )n +1\right ) }{\frac {1}{2} n \cdot \left (\frac {1}{2} n -1\right ) \cdot \ldots \cdot \left (\frac {1}{2}n-\left (1/2 -3\beta \right )n +1\right )}\ge 2^{\left (\frac {1}{2}-3\beta \right )n}.\end{equation*}

6. Concluding remarks

In this paper, we proved a near optimal lower bound on the number of Hamiltonian subsets in a graph with given minimum degree, which asymptotically gives much better bounds for large graphs. Kim et al. [13, Theorem 1.3] proved that for $d$ sufficiently large, any graph $G$ different from $K_{d+1}$ with minimum degree $\delta (G) \ge d$ has at least roughly twice as many Hamiltonian subsets as $K_{d+1}$ . The following extension of Komlós’s conjecture seems plausible.

Problem 6.1. Let $d\ge 3$ be an odd integer. Let $G$ be a graph different from $K_{d+1}$ with minimum degree $\delta (G) \ge d$ . Is $h(G) \ge 2 h(K_{d+1})$ ?

Equality occurs if $G\in \{ 2K_{d+1}, K_{d+1} \star K_{d+1}, K_{d+2} \backslash M\},$ where $M$ is a maximum-size matching of $K_{d+2},$ or when $G=K_{3,3}$ and $d=3$ . Here $K_{d+1} \star K_{d+1}$ is the union of two $K_{d+1}$ s which are vertex-disjoint except from one common vertex. Notice that the same is not true for even $d$ , as then

\begin{equation*}h(K_{d+2} \backslash M) = 2^{d+2}-d^2-\frac 72 d -4 \lt 2 h(K_{d+1})=2^{d+2}-d^2-3d -4.\end{equation*}