Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T10:14:47.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurable Events Indexed by Trees

Published online by Cambridge University Press:  12 March 2012

PANDELIS DODOS ,
VASSILIS KANELLOPOULOS  and
KONSTANTINOS TYROS
PANDELIS DODOS
Affiliation:
Department of Mathematics, University of Athens, Panepistimiopolis 157 84, Athens, Greece (e-mail: pdodos@math.uoa.gr)
VASSILIS KANELLOPOULOS
Affiliation:
National Technical University of Athens, Faculty of Applied Sciences, Department of Mathematics, Zografou Campus, 157 80, Athens, Greece (e-mail: bkanel@math.ntua.gr)
KONSTANTINOS TYROS
Affiliation:
Department of Mathematics, University of Toronto, Toronto, CanadaM5S 2E4 (e-mail: k.tyros@utoronto.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

A tree T is said to be homogeneous if it is uniquely rooted and there exists an integer b ≥ 2, called the branching number of T, such that every t ∈ T has exactly b immediate successors. We study the behaviour of measurable events in probability spaces indexed by homogeneous trees.

Precisely, we show that for every integer b ≥ 2 and every integer n ≥ 1 there exists an integer q(b,n) with the following property. If T is a homogeneous tree with branching number b and {At:t ∈ T} is a family of measurable events in a probability space (Ω,Σ,μ) satisfying μ(At)≥ϵ>0 for every t ∈ T, then for every 0<θ<ϵ there exists a strong subtree S of T of infinite height, such that for every finite subset F of S of cardinality n ≥ 1 we have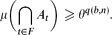 In fact, we can take q(b,n)= ((2b−1)2n−1−1)·(2b−2)−1. A finite version of this result is also obtained.

Keywords

Primary 05D1005C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 3 , May 2012 , pp. 374 - 411
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Blass, A. (1981) A partition theorem for perfect sets. Proc. Amer. Math. Soc. 82 271–277.CrossRefGoogle Scholar
[2]Dodos, P., Kanellopoulos, V. and Karagiannis, N. (2010) A density version of the Halpern–Läuchli theorem. Preprint, available at http://arxiv.org/abs/1006.2671.Google Scholar
[3]Carlson, T. J. (1988) Some unifying principles in Ramsey Theory. Discrete Math. 68 117–169.CrossRefGoogle Scholar
[4]Furstenberg, H. and Katznelson, Y. (1991) A density version of the Hales–Jewett theorem. J. Anal. Math. 57 64–119.CrossRefGoogle Scholar
[5]Galvin, F. (1968) Partition theorems for the real line. Notices Amer. Math. Soc. 15 660.Google Scholar
[6]Hales, A. H. and Jewett, R. I. (1963) Regularity and positional games. Trans. Amer. Math. Soc. 106 222–229.CrossRefGoogle Scholar
[7]Halpern, J. D. and Läuchli, H. (1966) A partition theorem. Trans. Amer. Math. Soc. 124 360–367.CrossRefGoogle Scholar
[8]Milliken, K. (1979) A Ramsey theorem for trees. J. Combin. Theory Ser. A 26 215–237.CrossRefGoogle Scholar
[9]Milliken, K. (1981) A partition theorem for the infinite subtrees of a tree. Trans. Amer. Math. Soc. 263 137–148.CrossRefGoogle Scholar
[10]Polymath, D. H. J. (2009) A new proof of the density Hales–Jewett theorem. Preprint, available at http://arxiv.org/abs/0910.3926.Google Scholar
[11]Ramsey, F. P. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.CrossRefGoogle Scholar
[12]Rose, H. E. (1984) Subrecursion: Functions and Hierarchies, Vol. 9 Oxford Logic Guides, Oxford University Press.Google Scholar
[13]Shelah, S. (1988) Primitive recursive bounds for van der Waerden numbers. J. Amer. Math. Soc. 1 683–697.CrossRefGoogle Scholar
[14]Sokić, M. (2011) Bounds on trees. Discrete Math. 311 398–407.CrossRefGoogle Scholar
[15]Todorcevic, S. (2010) Introduction to Ramsey Spaces, Vol. 174 of Annals of Mathematics Studies, Princeton University Press.Google Scholar