Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kannan, R.
1994.
Markov chains and polynomial time algorithms.
p.
656.
Dagum, P.
Karp, R.
Luby, M.
and
Ross, S.
1995.
An optimal algorithm for Monte Carlo estimation.
p.
142.
Luby, M.
1996.
Introduction to special issue on randomized and derandomized algorithms.
Algorithmica,
Vol. 16,
Issue. 4-5,
p.
359.
Saloff-Coste, Laurent
1997.
Lectures on Probability Theory and Statistics.
Vol. 1665,
Issue. ,
p.
301.
Kuznetsov, N. Yu.
1998.
Using stratified sampling to solve the knapsack problem.
Cybernetics and Systems Analysis,
Vol. 34,
Issue. 1,
p.
61.
Morris, B.
and
Sinclair, A.
1999.
Random walks on truncated cubes and sampling 0-1 knapsack solutions.
p.
230.
Goldberg, Paul W.
1999.
Learning fixed-dimension linear thresholds from fragmented data.
p.
88.
Dagum, Paul
Karp, Richard
Luby, Michael
and
Ross, Sheldon
2000.
An Optimal Algorithm for Monte Carlo Estimation.
SIAM Journal on Computing,
Vol. 29,
Issue. 5,
p.
1484.
Chawla, Deepak
Li, Lin
and
Scott, Stephen
2001.
Computational Learning Theory.
Vol. 2111,
Issue. ,
p.
82.
Goldberg, Paul W.
2001.
Computational Learning Theory.
Vol. 2111,
Issue. ,
p.
116.
Goldberg, Paul W
2001.
Learning Fixed-Dimension Linear Thresholds from Fragmented Data.
Information and Computation,
Vol. 171,
Issue. 1,
p.
98.
Dyer, Martin
2003.
Approximate counting by dynamic programming.
p.
693.
Morris, Ben
and
Sinclair, Alistair
2004.
Random Walks on Truncated Cubes and Sampling 0-1 Knapsack Solutions.
SIAM Journal on Computing,
Vol. 34,
Issue. 1,
p.
195.
Chawla, Deepak
Li, Lin
and
Scott, Stephen
2004.
On approximating weighted sums with exponentially many terms.
Journal of Computer and System Sciences,
Vol. 69,
Issue. 2,
p.
196.
Cryan, Mary
Dyer, Martin
and
Randall, Dana
2005.
Approximately counting integral flows and cell-bounded contingency tables.
p.
413.
Servedio, R.A.
2006.
Every Linear Threshold Function has a Low-Weight Approximator.
p.
18.
Goldberg, Paul W.
2006.
A Bound on the Precision Required to Estimate a Boolean Perceptron from Its Average Satisfying Assignment.
SIAM Journal on Discrete Mathematics,
Vol. 20,
Issue. 2,
p.
328.
Cryan, Mary
Dyer, Martin
and
Randall, Dana
2010.
Approximately Counting Integral Flows and Cell-Bounded Contingency Tables.
SIAM Journal on Computing,
Vol. 39,
Issue. 7,
p.
2683.
Gopalan, Parikshit
Klivans, Adam
Meka, Raghu
tefankovic, Daniel
Vempala, Santosh
and
Vigoda, Eric
2011.
An FPTAS for #Knapsack and Related Counting Problems.
p.
817.
Koppen, Mario
Yoshida, Kaori
and
Tsuru, Masato
2011.
Fuzzy Approaches to Proportional Fairness.
p.
72.

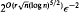 time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ±
time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ± 