Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T19:15:14.485Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimizing the number of 5-cycles in graphs with given edge-density

Part of: Graph theory

Published online by Cambridge University Press:  09 October 2019

Patrick Bennett ,
Andrzej Dudek ,
Bernard Lidický  and
Oleg Pikhurko
Patrick Bennett
Affiliation:
Department of Mathematics, Western Michigan University, Kalamazoo, MI 49008, USA
Andrzej Dudek*
Affiliation:
Department of Mathematics, Western Michigan University, Kalamazoo, MI 49008, USA
Bernard Lidický
Affiliation:
Department of Mathematics, Iowa State University, Ames, IA 50011, USA
Oleg Pikhurko
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, Coventry CV4 7AL, UK
*
*Corresponding author. email: andrzej.dudek@wmich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the work of Razborov about the minimal density of triangles in graphs we study the minimal density of the 5-cycle C5. We show that every graph of order n and size 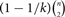$ (1 - 1/k) \left( {\matrix{n \cr 2 }} \right) $, where k ≥ 3 is an integer, contains at least

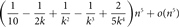$$({1 \over {10}} - {1 \over {2k}} + {1 \over {{k^2}}} - {1 \over {{k^3}}} + {2 \over {5{k^4}}}){n^5} + o({n^5})$$
copies of C5. This bound is optimal, since a matching upper bound is given by the balanced complete k-partite graph. The proof is based on the flag algebras framework. We also provide a stability result. An SDP solver is not necessary to verify our proofs.

MSC classification

Primary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 1 , January 2020 , pp. 44 - 67
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported in part by Simons Foundation grant 426894.

‡

Supported in part by Simons Foundation grant 522400.

§

Supported in part by NSF grant DMS-1600390.

Supported in part by ERC grant 306493.

References

Alon, N., Fischer, E., Krivelevich, M. and Szegedy, M. (2000) Efficient testing of large graphs. Combinatorica 20 451–476.10.1007/s004930070001CrossRefGoogle Scholar
Balogh, J., Hu, P., Lidický, B. and Pfender, F. (2016) Maximum density of induced 5-cycle is achieved by an iterated blow-up of 5-cycle. European J. Combin . 52 (A) 47–58.CrossRefGoogle Scholar
Borchers, B. (1999) CSDP, a C library for semidefinite programming. Optim. Methods Softw. 11 613–623.CrossRefGoogle Scholar
Conlon, D. and Fox, J. (2013) Graph removal lemmas. In Surveys in Combinatorics 2013, Vol. 409 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 1–49.Google Scholar
Erdös, P. (1984) On some problems in graph theory, combinatorial analysis and combinatorial number theory. In Graph Theory and Combinatorics (Cambridge, 1983), Academic Press, pp. 1–17.Google Scholar
Erdös, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc. 52 1087–1091.CrossRefGoogle Scholar
Frieze, A. and Karoński, M. (2016) Introduction to Random Graphs, Cambridge University Press.CrossRefGoogle Scholar
Grzesik, A. (2012) On the maximum number of five-cycles in a triangle-free graph. J. Combin. Theory Ser. B 102 1061–1066.CrossRefGoogle Scholar
Hatami, H., Hladký, J., Král’, D., Norine, S. and Razborov, A. (2013) On the number of pentagons in triangle-free graphs. J. Combin. Theory Ser. A 120 722–732.CrossRefGoogle Scholar
Lidický, B. and Pfender, F. (2018) Pentagons in triangle-free graphs. European J. Combin . 74 85–89.CrossRefGoogle Scholar
Liu, H., Pikhurko, O., Sharifzadeh, M. and Staden, K. (2019) Stability from symmetrisation arguments. Work in progress.Google Scholar
Liu, H., Pikhurko, O. and Staden, K. (2017) The exact minimum number of triangles in graphs of given order and size. arXiv:1712.00633Google Scholar
Lovász, L. (2012) Large Networks and Graph Limits, Colloquium Publications, American Mathematical Society.CrossRefGoogle Scholar
Lovász, L. and Simonovits, M. (1983) On the number of complete subgraphs of a graph, II. In Studies in Pure Mathematics (Erdös, P. et al., eds), Birkhäuser, pp. 459–495.10.1007/978-3-0348-5438-2_41CrossRefGoogle Scholar
Lovász, L. and Szegedy, B. (2006) Limits of dense graph sequences. J. Combin. Theory Ser. B 96 933–957.CrossRefGoogle Scholar
Lovász, L. and Szegedy, B. (2010) Testing properties of graphs and functions. Israel J. Math . 178 113–156.CrossRefGoogle Scholar
Mantel, W. (1907) Problem 28. Winkundige Opgaven 10 60–61.Google Scholar
Moon, J. W. and Moser, L. (1962) On a problem of Turán. Magyar Tud. Akad. Mat. Kutató Int. Közl. 7 283–286.Google Scholar
Nikiforov, V. (2011) The number of cliques in graphs of given order and size. Trans. Amer. Math. Soc. 363 1599–1618.CrossRefGoogle Scholar
Nordhaus, E. A. and Stewart, B. M. (1963) Triangles in an ordinary graph. Canad. J. Math. 15 33–41.CrossRefGoogle Scholar
Pikhurko, O. (2010) An analytic approach to stability. Discrete Math . 310 2951–2964.CrossRefGoogle Scholar
Pikhurko, O. and Razborov, A. (2017) Asymptotic structure of graphs with the minimum number of triangles. Combin. Probab. Comput. 26 138–160.CrossRefGoogle Scholar
Pikhurko, O., Sliacan, J. and Tyros, K. (2019) Strong forms of stability from flag algebra calculations. J. Combin. Theory Ser. B 135 129–178.CrossRefGoogle Scholar
Pippenger, N. and Golumbic, M. C. (1975) The inducibility of graphs. J. Combin. Theory Ser. B 19 189–203.CrossRefGoogle Scholar
Razborov, A. (2007) Flag algebras. J. Symbolic Logic 72 1239–1282.CrossRefGoogle Scholar
Razborov, A. (2008) On the minimal density of triangles in graphs. Combin. Probab. Comput. 17 603–618.CrossRefGoogle Scholar
Reiher, C. (2016) The clique density theorem. Ann. of Math. (2) 184 683–707.CrossRefGoogle Scholar
Sidorenko, A. (1991) Inequalities for functionals generated by bipartite graphs. Diskret. Mat. 3 50–65.Google Scholar
Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz. Lapok 48 436–452.Google Scholar