Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T22:05:36.862Z Has data issue: false hasContentIssue false
  • English
  • Français

The minimum perfect matching in pseudo-dimension 0 < q < 1

Part of: Graph theory Combinatorial probability

Published online by Cambridge University Press:  27 October 2020

Joel Larsson
Joel Larsson*
Affiliation:
Department of Statistics, Lund University, Lund, Scania, Sweden
*
Email: joel.larsson@stat.lu.se
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that for Kn,n equipped with i.i.d. exp (1) edge costs, the minimum total cost of a perfect matching converges to 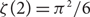$\zeta(2)=\pi^2/6$ in probability. Similar convergence has been established for all edge cost distributions of pseudo-dimension 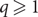$q \geq 1$ . In this paper we extend those results to all real positive q, confirming the Mézard–Parisi conjecture in the last remaining applicable case.

MSC classification

Primary: 05C80: Random graphs
Secondary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 374 - 397
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Aldous, D. J. (1992) Asymptotics in the random assignment problem. Probab. Theory Rel. Fields 93 507–534.Google Scholar
Aldous, D. J. (2001) The $\zeta(2)$ limit in the random assignment problem. Random Struct. Algorithms 18 381–418.Google Scholar
Aldous, D. and Steele, J. M. (2004) The objective method: probabilistic combinatorial optimization and local weak convergence. In Probability on Discrete Structures (Kesten, H., ed.), Vol. 110 of Encyclopaedia of Mathematical Sciences, pp. 1–72. Springer.Google Scholar
Karp, R. M. (1987) An upper bound on the expected cost of an optimal assignment. In Discrete Algorithms and Complexity, Vol. 15 of Perspectives in Computing, pp. 1–4. Academic Press.Google Scholar
Krokhmal, P. A. and Pardalos, P. M. (2009) Random assignment problems. European J. Oper. Res. 194 1–17.Google Scholar
Linusson, S. and Wästlund, J. (2004) A proof of Parisi’s conjecture on the random assignment problem. Probab. Theory Relat. Fields 128 419–440.Google Scholar
Lovász, L. (2012) Large Networks and Graph Limits, Vol. 60 of Colloquium Publications. American Mathematical Society.Google Scholar
Mézard, M. and Parisi, G. (1985) Replicas and optimization. J. Physique Lett. 46 L771–L778.Google Scholar
Nair, C., Prabhakar, B. and Sharma, M. (2005) Proofs of the Parisi and Coppersmith–Sorkin random assignment conjectures. Random Struct. Algorithms 27 413–443.Google Scholar
Parisi, G. (1998) A conjecture on random bipartite matching. arXiv:cond-mat/9801176v1Google Scholar
Salez, J. and Shah, D. (2009) Belief propagation: an asymptotically optimal algorithm for the random assignment problem. Math. Oper. Res. 34 468–480.Google Scholar
Walkup, D. W. (1979) On the expected value of a random assignment problem. SIAM J. Comput. 8 440–442.Google Scholar
Wästlund, J. (2005) A proof of a conjecture of Buck, Chan, and Robbins on the expected value of the minimum assignment. Random Struct. Algorithms 26 237–251.CrossRefGoogle Scholar
Wästlund, J. (2012) Replica symmetry of the minimum matching. Ann. of Math. 175 1061–1091.Google Scholar