Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-11T01:35:36.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Multicolour Sunflowers

Part of: Extremal combinatorics

Published online by Cambridge University Press:  22 April 2018

DHRUV MUBAYI  and
LUJIA WANG
DHRUV MUBAYI
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL 60607, USA (e-mail: mubayi@uic.edu, lwang203@uic.edu)
LUJIA WANG
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL 60607, USA (e-mail: mubayi@uic.edu, lwang203@uic.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

A sunflower is a collection of distinct sets such that the intersection of any two of them is the same as the common intersection C of all of them, and |C| is smaller than each of the sets. A longstanding conjecture due to Erdős and Szemerédi (solved recently in [7, 9]; see also [22]) was that the maximum size of a family of subsets of [n] that contains no sunflower of fixed size k > 2 is exponentially smaller than 2n as n → ∞. We consider the problems of determining the maximum sum and product of k families of subsets of [n] that contain no sunflower of size k with one set from each family. For the sum, we prove that the maximum is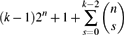

$$(k-1)2^n+1+\sum_{s=0}^{k-2}\binom{n}{s}$$
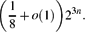for all n ⩾ k ⩾ 3, and for the k = 3 case of the product, we prove that the maximum is
$$\biggl(\ffrac{1}{8}+o(1)\biggr)2^{3n}.$$
 We conjecture that for all fixed k ⩾ 3, the maximum product is (1/8+o(1))2kn.

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 6 , November 2018 , pp. 974 - 987
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research partially supported by NSF grants DMS-0969092 and DMS-1300138.

References

[1] Alon, N., Shpilka, A. and Umans, C. (2013) On sunflowers and matrix multiplication. Comput. Complexity 22 219–243.Google Scholar
[2] Bey, C. (2005) On cross-intersecting families of sets. Graphs Combin. 21 161–168.Google Scholar
[3] Bollobás, B., Keevash, P. and Sudakov, B. (2004) Multicolored extremal problems. J. Combin. Theory Ser. A 107 295–312.Google Scholar
[4] Borg, P. (2008) Intersecting and cross-intersecting families of labeled sets. Electron. J. Combin. 15 #N9.Google Scholar
[5] Borg, P. (2014) The maximum sum and the maximum product of sizes of cross-intersecting families. Europ. J. Combin. 35 117–130.Google Scholar
[6] Boyd, S. and Vandenberghe, L. (2004) Convex Optimization, Cambridge University Press.Google Scholar
[7] Croot, E., Lev, V. and Pach, P. (2017) Progression-free sets in ℤ4n are exponentially small. Ann. Math. 185 331–337.Google Scholar
[8] Deza, M. (1973) Une propriété extrémale des plans projectifs finis dans une classe de codes équidistants. Discrete Math. 6 343–352.Google Scholar
[9] Ellenberg, J. and Gijswijt, D. (2017) On large subsets of 𝔽qn with no three-term arithmetic progression. Ann. Math. 185 339–343.Google Scholar
[10] Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. 12 313–320.Google Scholar
[11] Erdős, P. and Rado, R. (1960) Intersection theorems for systems of sets. J. London Math. Soc. 35 85–90.Google Scholar
[12] Erdős, P. and Szemerédi, E. (1978) Combinatorial properties of systems of sets. J. Combin. Theory Ser. A 24 308–313.Google Scholar
[13] Frankl, P. and Rödl, V. (1987) Forbidden intersections. Trans. Amer. Math. Soc. 300 259–286.Google Scholar
[14] Frankl, P. and Tokushige, N. (2011) On r-cross intersecting families of sets. Combin. Probab. Comput. 20 749–752.Google Scholar
[15] Frankl, P., Lee, S. J., Siggers, M. and Tokushige, N. (2014) An Erdős–Ko–Rado theorem for cross t-intersecting families. J. Combin. Theory Ser. A 128 207–249.Google Scholar
[16] Hilton, A. J. W. (1977) An intersection theorem for a collection of families of subsets of a finite set. J. London Math. Soc. 2 369–384.Google Scholar
[17] Keevash, P., Saks, M., Sudakov, B. and Verstraëte, J. (2004) Multicolor Turán problems. Adv. Appl. Math. 33 238–262.Google Scholar
[18] Keevash, P. and Sudakov, B. (2005) Set systems with restricted cross-intersections and the minimum rank of inclusion matrices. SIAM J. Discrete Math. 18 713–727.Google Scholar
[19] van Lint, J. H. (1973) A theorem on equidistant codes. Discrete Math. 6 353–358.Google Scholar
[20] Matsumoto, M. and Tokushige, N. (1989) The exact bound in the Erdős–Rado–Ko theorem for cross-intersecting families. J. Combin. Theory Ser. A 52 90–97.Google Scholar
[21] Mubayi, D. and Rödl, V. (2014) Specified intersections. Trans. Amer. Math. Soc. 366 491–504.Google Scholar
[22] Naslund, E. and Sawin, W. F. (2017) Upper bounds for sunflower-free sets. Forum Math., Sigma 5 E15. doi:10.1017/fms.2017.12Google Scholar
[23] Pyber, L. (1986) A new generalization of the Erdős–Ko–Rado theorem. J. Combin. Theory Ser. A 43 85–90.Google Scholar