Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T21:30:34.469Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-perfect clique-factors in sparse pseudorandom graphs

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  11 December 2020

Jie Han ,
Yoshiharu Kohayakawa  and
Yury Person
Jie Han
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, China
Yoshiharu Kohayakawa
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, Brazil
Yury Person*
Affiliation:
Institut für Mathematik, Technische Universität Ilmenau, 98684 Ilmenau, Germany
*
*Corresponding author. Email: yury.person@tu-ilmenau.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, for any 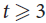$t \ge 3$, there exists a constant c = c(t) > 0 such that any d-regular n-vertex graph with the second largest eigenvalue in absolute value λ satisfying 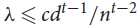$\lambda \le c{d^{t - 1}}/{n^{t - 2}}$ contains vertex-disjoint copies of kt covering all but at most 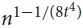${n^{1 - 1/(8{t^4})}}$ vertices. This provides further support for the conjecture of Krivelevich, Sudakov and Szábo (Combinatorica24 (2004), pp. 403–426) that (n, d, λ)-graphs with n ∈ 3ℕ and 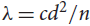$\lambda \le c{d^2}/n$ for a suitably small absolute constant c > 0 contain triangle-factors. Our arguments combine tools from linear programming with probabilistic techniques, and apply them in a certain weighted setting. We expect this method will be applicable to other problems in the field.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05D40: Probabilistic methods 90C35: Programming involving graphs or networks
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 4 , July 2021 , pp. 570 - 590
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

JH was supported by FAPESP (2014/18641-5, 2013/03447-6).

‡

YK was partially supported by CNPq (311412/2018-1, 423833/2018-9) and FAPESP (2018/04876-1).

§

YP was supported by DFG grant PE 2299/1-1.

The cooperation of the authors was supported by a joint CAPES-DAAD PROBRAL project (project 430/15, 57350402, 57391197). This research was partially supported by CAPES (Finance Code 001). FAPESP is the São Paulo Research Foundation. CNPq is the National Council for Scientific and Technological Development of Brazil.

References

Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. (2016) Blow-Up lemmas for sparse graphs. arXiv:1612.00622Google Scholar
Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. (2017) Powers of Hamilton cycles in pseudorandom graphs. Combinatorica 37 573–616.CrossRefGoogle Scholar
Alon, N. (1994) Explicit Ramsey graphs and orthonormal labelings. Electron. J. Combin. 1 R12.CrossRefGoogle Scholar
Alon, N. and Chung, F. R. K. (1988) Explicit construction of linear sized tolerant networks. Discrete Math. 72 15–19.CrossRefGoogle Scholar
Alon, N., Frankl, P., Huang, H., Rödl, V., Ruciński, A. and Sudakov, B. (2012) Large matchings in uniform hypergraphs and the conjectures of Erdös and Samuels. J. Combin. Theory Ser. A 119 1200–1215.CrossRefGoogle Scholar
Alon, N. and Kahale, N. (1998) Approximating the independence number via the θ-function. Math. Program. 80 253–264.CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The Probabilistic Method, fourth edition. Wiley.Google Scholar
Bollobás, B. (1998) Modern Graph Theory, Vol. 184 of Graduate Texts in Mathematics. Springer.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Zhao, Y. (2014) Extremal results in sparse pseudorandom graphs. Adv. Math. 256 206–290.CrossRefGoogle Scholar
Devlin, P. and Kahn, J. (2017) Perfect fractional matchings in k-out hypergraphs. Electron. J. Combin. 24 P3.60.CrossRefGoogle Scholar
Füredi, Z. (1988) Matchings and covers in hypergraphs. Graphs Combin. 4 115–206.CrossRefGoogle Scholar
Han, J. (2020) On perfect matchings in k-complexes. Int. Math. Res. Not. rnz343.CrossRefGoogle Scholar
Han, J., Kohayakawa, Y., Morris, P. and Person, Y. (2019) Clique-Factors in sparse pseudorandom graphs. European J. Combin. 82 102999.CrossRefGoogle Scholar
Han, J., Kohayakawa, Y. and Person, Y. (2018) Near-Perfect clique-factors in sparse pseudorandom graphs. In Discrete Mathematics Days 2018: Extended abstracts of the 11th ‘Jornadas de matemática discreta y algortmica’ (JMDA), Seville 2018, pp. 221–226. Elsevier.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs. Wiley-Interscience.CrossRefGoogle Scholar
Keevash, P. and Mycroft, R. (2015) A Geometric Theory for Hypergraph Matching, Vol. 233, no. 1098 of Memoirs of the American Mathematical Society. AMS.Google Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1997) Blow-Up lemma. Combinatorica 17 109–123.CrossRefGoogle Scholar
Kostochka, A. V. and Rödl, V. (1998) Partial Steiner systems and matchings in hypergraphs. Random Struct. Algorithms 13 335–347.3.0.CO;2-W>CrossRefGoogle Scholar
Krivelevich, M. (1996) Perfect fractional matchings in random hypergraphs. Random Struct. Algorithms 9 317–334.3.0.CO;2-#>CrossRefGoogle Scholar
Krivelevich, M. and Sudakov, B. (2006) Pseudo-Random graphs. In More Sets, Graphs and Numbers, Vol. 15 of Bolyai Society Mathematical Studies, pp. 199–262. Springer.CrossRefGoogle Scholar
Krivelevich, M., Sudakov, B. and Szabó, T. (2004) Triangle factors in sparse pseudo-random graphs. Combinatorica 24 403–426.CrossRefGoogle Scholar
Matoušek, J. and Gärtner, B. (2007) Understanding and Using Linear Programming. Springer.Google Scholar
Nenadov, R. (2019) Triangle-Factors in pseudorandom graphs. Bull. Lond. Math. Soc. 51 421–430.CrossRefGoogle Scholar
Rödl, V. (1985) On a packing and covering problem. European J. Combin. 6 69–78.CrossRefGoogle Scholar
Sudakov, B., Szabó, T. and Vu, V. (2005) A generalization of Turán’s theorem. J. Graph Theory 49 187–195.CrossRefGoogle Scholar