Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T22:18:11.798Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on distinct distances

Part of: Extremal combinatorics Discrete geometry

Published online by Cambridge University Press:  16 July 2020

Orit E. Raz
Orit E. Raz*
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Givat Ram, Jerusalem 91904, Israel, Email: oritraz@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that, for a constant-degree algebraic curve γ in ℝD, every set of n points on γ spans at least Ω(n4/3) distinct distances, unless γ is an algebraic helix, in the sense of Charalambides [2]. This improves the earlier bound Ω(n5/4) of Charalambides [2].

We also show that, for every set P of n points that lie on a d-dimensional constant-degree algebraic variety V in ℝD, there exists a subset S ⊂ P of size at least Ω(n4/(9+12(d−1))), such that S spans 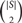$\left({\begin{array}{*{20}{c}} {|S|} \\ 2 \\\end{array}} \right)$ distinct distances. This improves the earlier bound of Ω(n1/(3d)) of Conlon, Fox, Gasarch, Harris, Ulrich and Zbarsky [4].

Both results are consequences of a common technical tool.

MSC classification

Primary: 52C10: Erdős problems and related topics of discrete geometry
Secondary: 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 5 , September 2020 , pp. 650 - 663
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Work on this paper was supported by Grant 892/13 from the Israel Science Foundation, by the Israeli Centers of Research Excellence (I-CORE) program (Center No. 4/11), and by a Shulamit Aloni Fellowship from the Israeli Ministry of Science.

References

Brass, P., Moser, W. and Pach, J. (2005) Research Problems in Discrete Geometry, Springer.Google Scholar
Charalambides, M. (2014) Distinct distances on curves via rigidity. Discrete Comput. Geom. 51 666–701.CrossRefGoogle Scholar
Charalambides, M. (2013) A note on distinct distance subsets, J. Geom. 104 439–442.CrossRefGoogle Scholar
Conlon, D., Fox, J., Gasarch, W., Harris, D. G., Ulrich, D. and Zbarsky, S. (2015) Distinct volume subsets. SIAM J. Discrete Math. 29 472–480.CrossRefGoogle Scholar
D’Angelo, J. P. and Tyson, J. T. (2009) Helical CR structures and sub-Riemannian geodesics. Complex Var. Elliptic Equ. 54 205–221.CrossRefGoogle Scholar
Elekes, G. and Rónyai, L. (2000) A combinatorial problem on polynomials and rational functions. J. Combin. Theory Ser. A 89 1–20.CrossRefGoogle Scholar
Elekes, G. and Szabó, E. (2012) How to find groups? (And how to use them in Erdös geometry?) Combinatorica 32 537–571.CrossRefGoogle Scholar
Erdös, P. (1946) On sets of distances of n points. Amer. Math. Monthly 53 248–250.CrossRefGoogle Scholar
Erdös, P. and Turán, P. (1941) On a problem of Sidon in additive number theory, and on some related problems. J. London Math. Soc. 1.4 212–215.CrossRefGoogle Scholar
Guth, L. and Katz, N. H. (2015) On the Erdös distinct distances problem in the plane. Ann. of Math. 181 155–190.CrossRefGoogle Scholar
Komlós, J., Sulyok, M. and Szemerédi, E. (1975) Linear problems in combinatorial number theory. Acta Math. Acad. Sci. Hungar. 26 113–121.CrossRefGoogle Scholar
Pach, J. and de Zeeuw, F. (2017) Distinct distances on algebraic curves in the plane. Combin. Probab. Comput. 26 99–117.CrossRefGoogle Scholar
Raz, O. E., Sharir, M. and de Zeeuw, F. (2016) Polynomials vanishing on Cartesian products: the Elekes–Szabó theorem revisited. Duke Math. J. 165.18 3517–3566.CrossRefGoogle Scholar
Sharir, M., Sheffer, A. and Solymosi, J. (2013) Distinct distances on two lines. J. Combin. Theory Ser. A 120 1732–1736.CrossRefGoogle Scholar
Thiele, T. (1995) Geometric selection problems and hypergraphs. PhD thesis, Institut für Mathematik, Freie Universität Berlin.Google Scholar
Youla, D. C. (1961) A normal form for a matrix under the unitary congruence group. Canad. J. Math. 13 694–704.CrossRefGoogle Scholar