Article contents
A note on the Brown–Erdős–Sós conjecture in groups
Published online by Cambridge University Press: 03 February 2020
Abstract
We show that a dense subset of a sufficiently large group multiplication table contains either a large part of the addition table of the integers modulo some k, or the entire multiplication table of a certain large abelian group, as a subgrid. As a consequence, we show that triples systems coming from a finite group contain configurations with t triples spanning 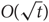 $ O(\sqrt t )$ vertices, which is the best possible up to the implied constant. We confirm that for all t we can find a collection of t triples spanning at most t + 3 vertices, resolving the Brown–Erdős–Sós conjecture in this context. The proof applies well-known arithmetic results including the multidimensional versions of Szemerédi’s theorem and the density Hales–Jewett theorem.
$ O(\sqrt t )$ vertices, which is the best possible up to the implied constant. We confirm that for all t we can find a collection of t triples spanning at most t + 3 vertices, resolving the Brown–Erdős–Sós conjecture in this context. The proof applies well-known arithmetic results including the multidimensional versions of Szemerédi’s theorem and the density Hales–Jewett theorem.
This result was discovered simultaneously and independently by Nenadov, Sudakov and Tyomkyn [5], and a weaker result avoiding the arithmetic machinery was obtained independently by Wong [11].
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2020
References
- 3
- Cited by


